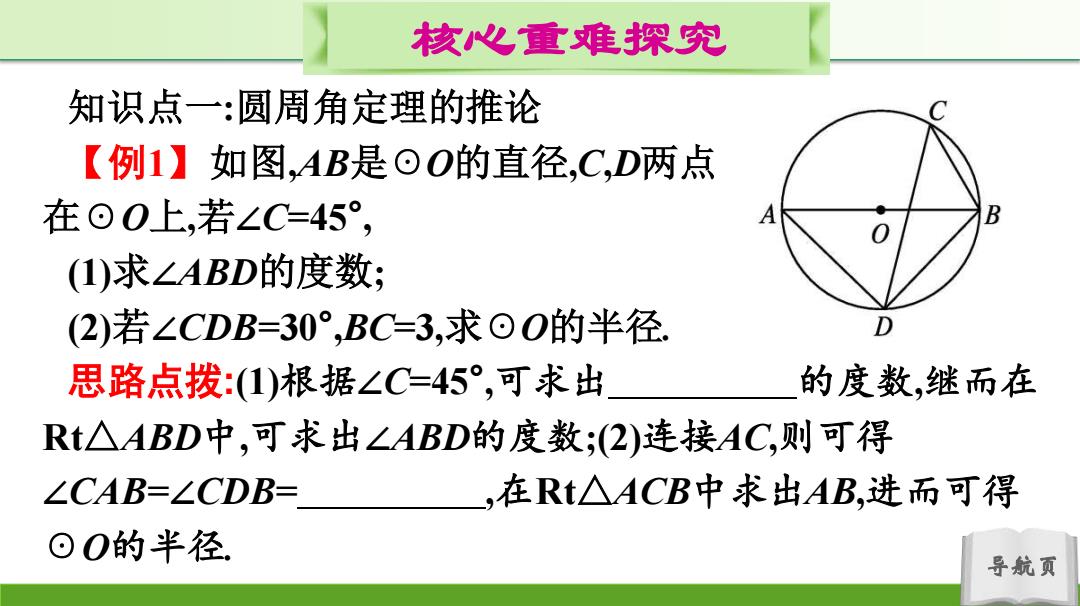
核心重难探究 知识点一:圆周角定理的推论 【例1】如图,AB是⊙O的直径,C,D两点 在⊙0上,若∠C=45°, B (1)求∠ABD的度数; (2)若∠CDB=30°,BC=3,求⊙O的半径 D 思路点拨:(1)根据∠C=45°,可求出 的度数,继而在 Rt△ABD中,可求出∠ABD的度数;2)连接AC,则可得 ∠CAB=∠CDB= ,在Rt△ACB中求出AB,进而可得 ⊙O的半径 导航页
导航页 核心重难探究 知识点一:圆周角定理的推论 【例1】如图,AB是☉O的直径,C,D两点 在☉O上,若∠C=45° , (1)求∠ABD的度数; (2)若∠CDB=30° ,BC=3,求☉O的半径. 思路点拨:(1)根据∠C=45° ,可求出 的度数,继而在 Rt△ABD中,可求出∠ABD的度数;(2)连接AC,则可得 ∠CAB=∠CDB= ,在Rt△ACB中求出AB,进而可得 ☉O的半径
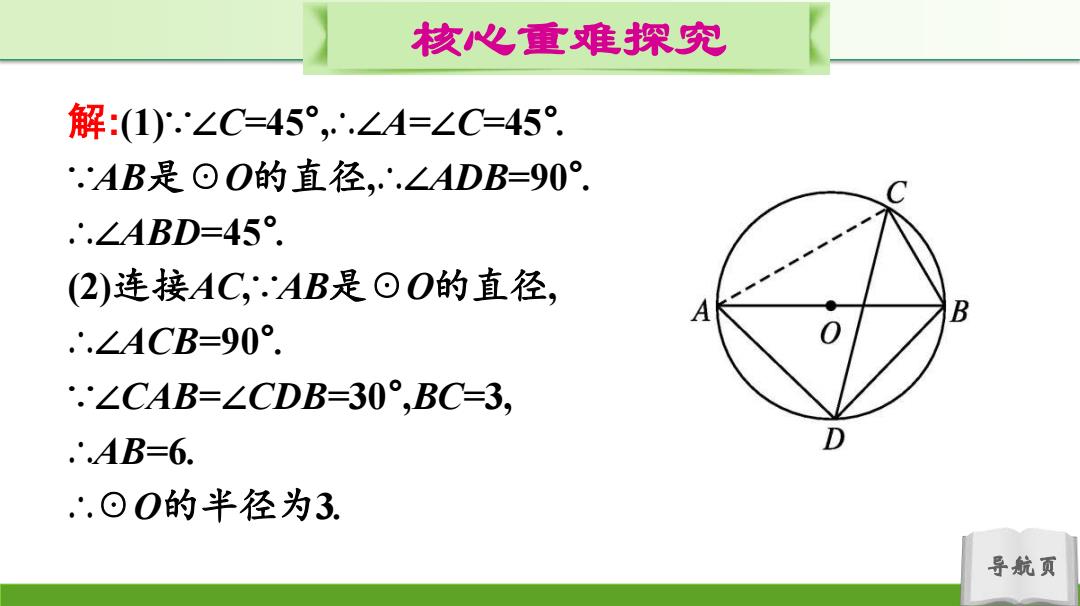
核心重难探究 解:1)∠C=45°,∴∠A=∠C=45°. .AB是回O的直径,∴.∠ADB=90°. ..∠ABD=45°. (2)连接AC,.AB是⊙O的直径, B .∴.∠ACB=90°. .'∠CAB=∠CDB=30°,BC=3, ‘AB=6. D .⊙0的半径为3. 导航页
导航页 核心重难探究 解:(1)∵∠C=45° ,∴∠A=∠C=45° . ∵AB是☉O的直径,∴∠ADB=90° . ∴∠ABD=45° . (2)连接AC,∵AB是☉O的直径, ∴∠ACB=90° . ∵∠CAB=∠CDB=30° ,BC=3, ∴AB=6. ∴☉O的半径为3

核心重难探究 【方法归纳】 在解圆的有关问题时,常常需要添加辅助线,构成直径所对 的圆周角,这种基本技能一定要掌握 导航页
导航页 核心重难探究 【方法归纳】 在解圆的有关问题时,常常需要添加辅助线,构成直径所对 的圆周角,这种基本技能一定要掌握