
(2)变形:变形协调条件(求补充方程)可选取固定端B为多余约束,予以解除,在该处的施加对应的约束反力FB,得到一个作用有原荷载和多余未知力的静定结构-称为原超静定结构的基本静定系或相当系统Y注意原超静定结构的B端约束情况,相当系统要保持和原结构相等,则相当系统在BC点的位移为零。F△β = 0即得变形协调条件TB15
(2)变形:变形协调条件(求补充方程) 可选取固定端 B 为多余约束,予以解除,在 该处的施加对应的约束反力FB,得到一个作用有原 荷载和多余未知力的静定结构 -称为原超静定结构的基本静定系或相当系统 注意原超静定结构的 B 端 约束情况,相当系统要保持和 原结构相等,则相当系统在 B 点的位移为零。 即得变形协调条件 B = 0 B F F B C A
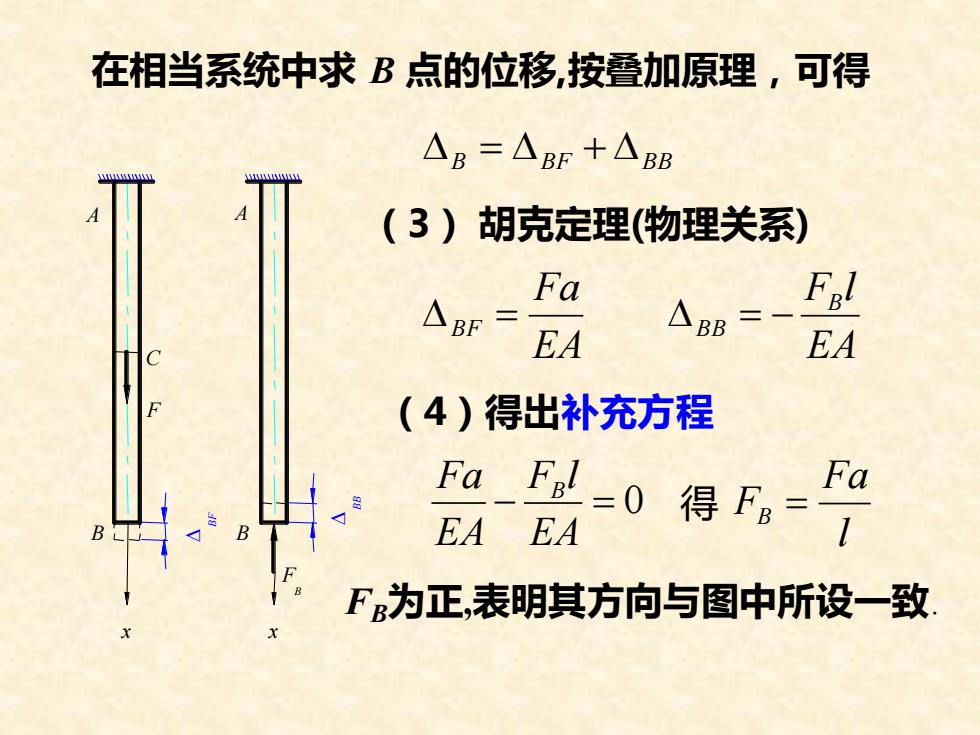
在相当系统中求B点的位移,按叠加原理,可得β =BF +BB(3)胡克定理(物理关系)FaFe!BBBFEAEAF(4)得出补充方程Fa FaFBl0得 FB-1EAEABFF为正,表明其方向与图中所设一致
在相当系统中求 B 点的位移,按叠加原理,可得 B = BF + BB (3) 胡克定理(物理关系) EA Fa BF = EA F l B BB = − (4)得出补充方程 − = 0 EA F l EA Fa B 得 l Fa FB = FB为正,表明其方向与图中所设一致. x F B C A BF x F B B A BB

例设1,2,3杆用铰连接如图,1、2两杆的长度、横截面面积和材料均相同,即l=l=l,A,=A,=A,Ei=E,=E;3杆长度为l,横截面面积为A3,弹性模量为E,试求各杆的轴力。DB解:一次超静定问题3(1)力:由节点A的平衡条件列出平衡方程αaAEF =0, - Fn sin α+ Fn2 sin α= 0FZF, = 0O, Fn3 +Fni coSα + Fn3 cosα - F = 0x
例 设l,2,3杆用铰连接如图,1、2两杆的长度、横 截面面积和材料均相同,即l1=l2=l,A1=A2 =A, E1= E2=E;3杆长度为l3 ,横截面面积为A3,弹性模量为 E3 ,试求各杆的轴力。 解:一次超静定问题 (1)力:由节点A的平衡条件列 出平衡方程 Fx = 0, − FN1 sin a + FN2 sin a = 0 Fy = 0,FN3 + FN1 cosa + FN3 cosa − F = 0 B D C A 1 3 2 F A F a a F F F N2 N3 N1 y x
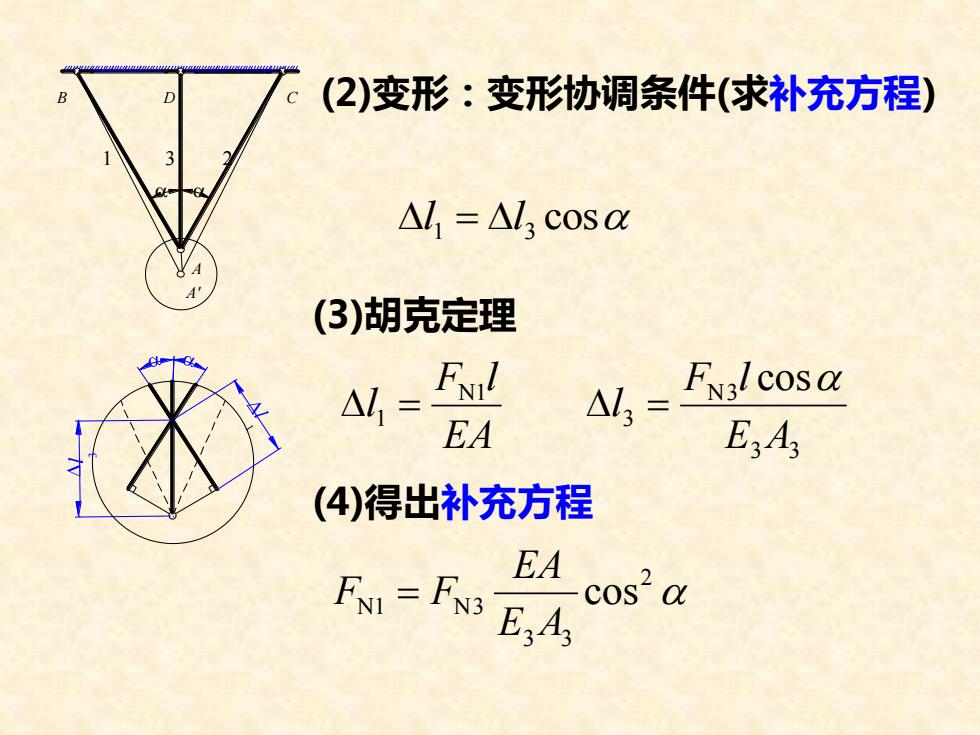
(2)变形:变形协调条件(求补充方程)Nl, = △l, cos α(3)胡克定理FN!Fn3l cosαAlAl,EAE,A,(4)得出补充方程EAcos’ αF.= Fn3N1E,A
(2)变形:变形协调条件(求补充方程) l 1 = l 3 cosa (3)胡克定理 EA F l l N1 1 = 3 3 N3 3 cos E A F l l a = l 3 B 1 a a 3 2 D C A A' (4)得出补充方程 a 2 3 3 N1 N3 cos E A EA F = F

联立平衡方程、补充方程,求解得FFn1 = Fn2 =E,A2 cosα +EAcos"αFFN3EA1+2cosQE,As在超静定杆系中,各杆轴力的大小和该杆的刚度与其它杆的刚度的比值有关增大或减少1、2两杆的刚度,则它们的轴力也将随之增大或减少;杆系中任一杆的刚度的改变都将引起杆系各轴力的重新分配。这些特点在静定杆系中是不存在的
联立平衡方程、补充方程,求解得 a a 2 3 3 N1 N2 cos 2cos EA E A F F F + = = a 3 3 3 N3 1 2 cos E A EA F F + = 在超静定杆系中,各杆轴力的大小和该杆的刚度 与其它杆的刚度的比值有关 增大或减少1、2两杆的刚度,则它们的轴力也将 随之增大或减少;杆系中任一杆的刚度的改变都将 引起杆系各轴力的重新分配。这些特点在静定杆系 中是不存在的