
离散傅里叶变换的性质 ▣序列的圆周移位一—时域、频域(调制) xm(n)=x((n+m))N Ry (n) 充分理解表达式的含义 √有限长序列延拓成周期序列,对周期序列移位 √取主值区间(0~N-1)的值。 X(k)=Wmkx(k) 圆周移位导致频谱线性相移,对频谱幅度无影响 调制特性DFTWMx(川=X(k+I)xRw(k) 时域序列的调制等效于频域的圆周移位
有限长序列延拓成周期序列,对周期序列移位 取主值区间(0~N-1)的值。 序列的圆周移位——时域、频域(调制) ( ) (( )) ( ) m NN x n xn m R n 圆周移位导致频谱线性相移,对频谱幅度无影响 () () mk Xm N k W Xk 离散傅里叶变换的性质 充分理解表达式的含义 调制特性 时域序列的调制等效于频域的圆周移位 DFT[ ( )] (( )) ( ) nl W xn X k l R k N NN
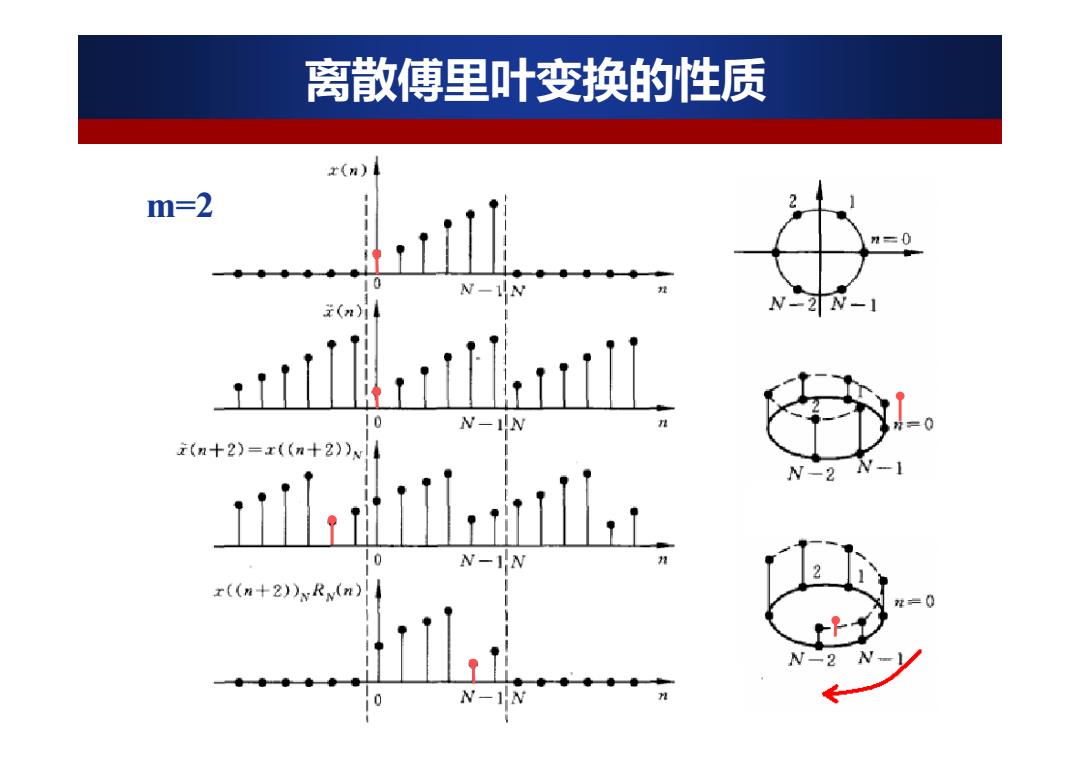
离散傅里叶变换的性质 x(n) m=2 n=0 0 (n)i N2N-1 N-IN i(n十2)=x((n+2))x N-2 N-IN ((n+2))xRM(n) 0
m=2 离散傅里叶变换的性质

离散傅里叶变换的性质 ▣对偶性 DFT[x(n)=X(k) DFTIX(n)]=Nx((-k))N Ry (k) =Nx((N-k))R(k)
对偶性 DFT[ ( )] ( ) xn Xk DFT[ ( )] (( )) ( ) (( )) ( ) N N N N X n Nx k R k Nx N k R k 离散傅里叶变换的性质

离散傅里叶变换的性质 圆周共轭对称性 回顾一下学过的共轭对称性(DTFT) x(n)=x.(n)+x(n) 共轭对称分量x.(m)=x(-m)=号[x(m)+x(-m 共轭反对称分量x,(n)=-x,(-)=x()-x(-川 [Refx.(n)=Re{x.(-n)Refx(n)=-Refx,(-n)} Im{x.(m)}=-lm{x.(-n)Im{x,(w)}=Im{x,(-m)}
圆周共轭对称性 () () () e o x n xn xn * * 1 ( ) ( ) [ ( ) ( )] 2 e e x n x n xn x n * * 1 ( ) ( ) [ ( ) ( )] 2 o o x n x n xn x n 离散傅里叶变换的性质 回顾一下学过的共轭对称性(DTFT) 共轭对称分量 共轭反对称分量 Re ( ) Re ( ) Im ( ) Im ( ) e e e e x n xn x n xn Re ( ) Re ( ) Im ( ) Im ( ) o o o o x n xn x n xn

离散傅里叶变换的性质 圆周共轭对称性 回顾一下学过的共轭对称性(DTFT) x(n)=x.(n)+x,(n) x.←mr→Re{X(e)} x,(←mr→jIm{X(e)} x(n)=Re{x(n)+jIm{x(n) ke{x(n→{x(e)+X'(e》-x.(e) Im{4xm以mm→2{x(e)-x(e》=x(e) 有什么用? 减少运算量
圆周共轭对称性 () () () e o x n xn xn 离散傅里叶变换的性质 回顾一下学过的共轭对称性(DTFT) DTFT ( ) Re jw e xn Xe DTFT ( ) Im jw o xn j Xe xn xn j xn ( ) Re ( ) Im ( ) 1 * Re ( ) = 2 DTFT jw jw jw e xn X e X e X e 1 1 * Im ( ) = 2 DTFT jw jw jw o xn X e X e X e j j 有什么用? 减少运算量