
信号处理理论与算法 时频分析-信号分析基础 张朋 自动化工程学院 1
信号处理理论与算法 时频分析-信号分析基础 张 朋 自动化工程学院 1
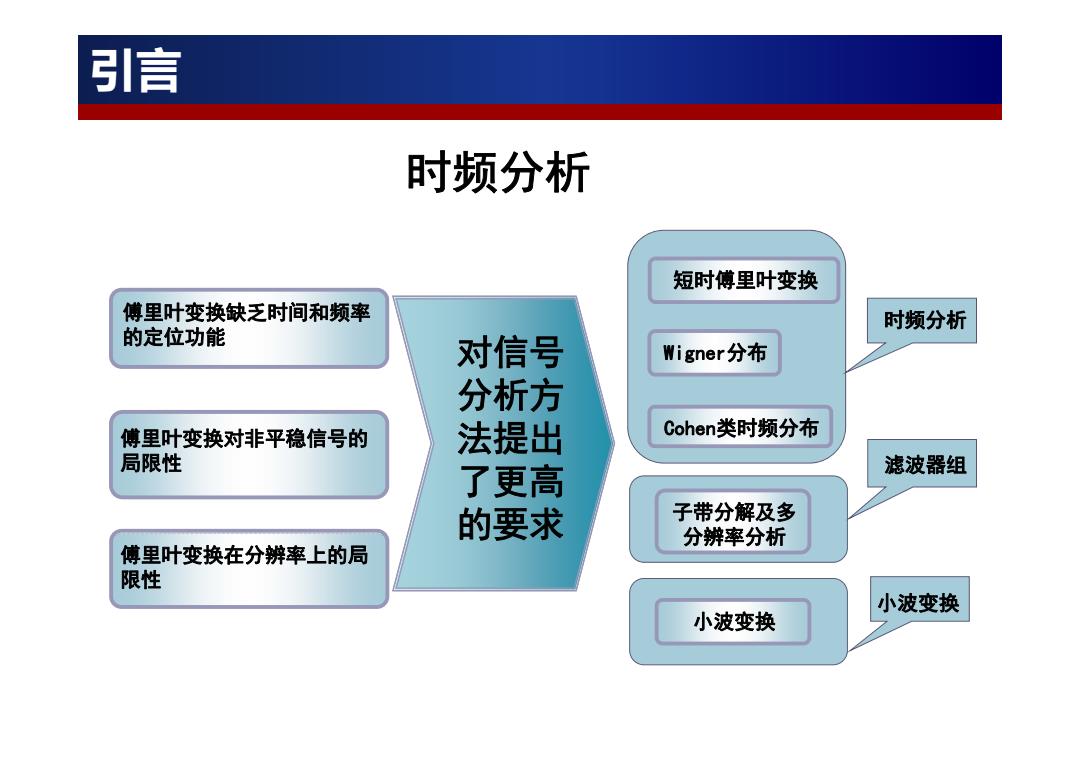
引言 时频分析 短时傅里叶变换 傅里叶变换缺乏时间和频率 时频分析 的定位功能 对信号 Wi gner分布 分析方 傅里叶变换对非平稳信号的 法提出 Cohen类时频分布 局限性 了更高 滤波器组 的要求 子带分解及多 分辨率分析 傅里叶变换在分辨率上的局 限性 小波变换 小波变换
傅里叶变换缺乏时间和频率 的定位功能 傅里叶变换对非平稳信号的 局限性 傅里叶变换在分辨率上的局 限性 对信号 分析方 法提出 了更高 的要求 短时傅里叶变换 Wigner分布 Cohen类时频分布 小波变换 子带分解及多 分辨率分析 时频分析 滤波器组 小波变换 时频分析 引言

信号的时-频联合分析 傅里叶变换 Kj2)=∫mx(0)et x0=元X(U2ed 傅里叶变换联系了时间和频率。但是,傅里叶变换存在三 方面不足。 傅里叶变换在时间、频率“定位”的不足 如要求在某一频率点处的值 X(U2)=∫xt)emdl 需要从-00~+0 如要求在某时刻处的值 需要2=-0~+0 x)=2元X(U2ed2
( ) () j t X j x t e dt 1 () ( ) 2 j t x t Xj e d 傅里叶变换联系了时间和频率。但是,傅里叶变换存在三 方面不足。 傅里叶变换 信号的时-频联合分析 傅里叶变换在时间、频率“定位”的不足 0 0 ( ) () j t X j x t e dt 0 0 1 () ( ) 2 j t x t X j e d 如要求在某一频率点处的值 需要t从 - ~+ 如要求在某时刻处的值 需要 =- ~+

信号的时-频联合分析 傅里叶变换在时间、频率“定位”的不足 设信号x()由三个不同频率的正弦所组成,即 sin(o,m),0≤n≤N1-1 x(nm={sin(o,n),N,≤n≤N2-1 sin(o,n),N2≤n≤N-1 N>N2>N,03>02>, 对x()做傅里叶变换,频谱x(e)是什么样? Linear scale Signal in time 0 ISTFT2,Lh-48.Nf-192,lin.scale,contour,Thld-5% 0.4 0.3 04 02 0.2 01 Freosoncy 0.1 0 159517975 0 50 100 150200250300 350 Time [s]
设信号x(n)由三个不同频率的正弦所组成,即 1 2 3 sin( ), ( ) sin( ), sin( ), n x n n n 1 1 2 2 0 1 1 1 n N N nN N nN 2 13 2 1 NN N , 对x(n)做傅里叶变换,频谱 是什么样? X e j 傅里叶变换在时间、频率“定位”的不足 信号的时-频联合分析
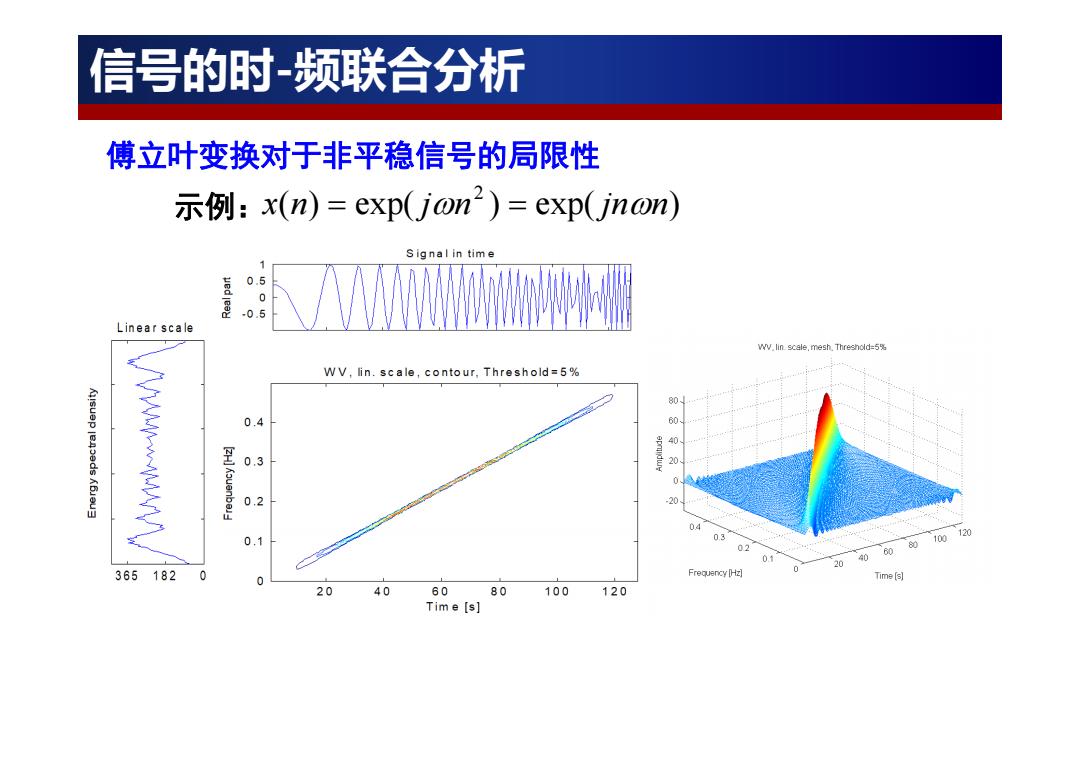
信号的时-频联合分析 傅立叶变换对于非平稳信号的局限性 示例:x(n)=exp(jon2)=exp(jnon) Signal in time 0 0 Linear scale WV.lin scale,mesh.Threshold=5% WV,lin.scale,contour,Threshold=5% 0.4 60 40 0.3 0 0.2 -20 04 120 0.1 03 02 80100 01 20 9060 365 182 0 Frequency [Hz] Time [s] 20 40 60 80 100 120 Time [s]
傅立叶变换对于非平稳信号的局限性 信号的时-频联合分析 示例: ( ) exp( ) exp( ) 2 x n j n jn n