特别地,称Q-A为A 的对立事件(或A的 逆事件、补事件)等, A 记成A A就是A不发生。 A 例1(续)A={1},B={2,4,6},于是 A1={2,3,4,5,6} B=1,3,5}
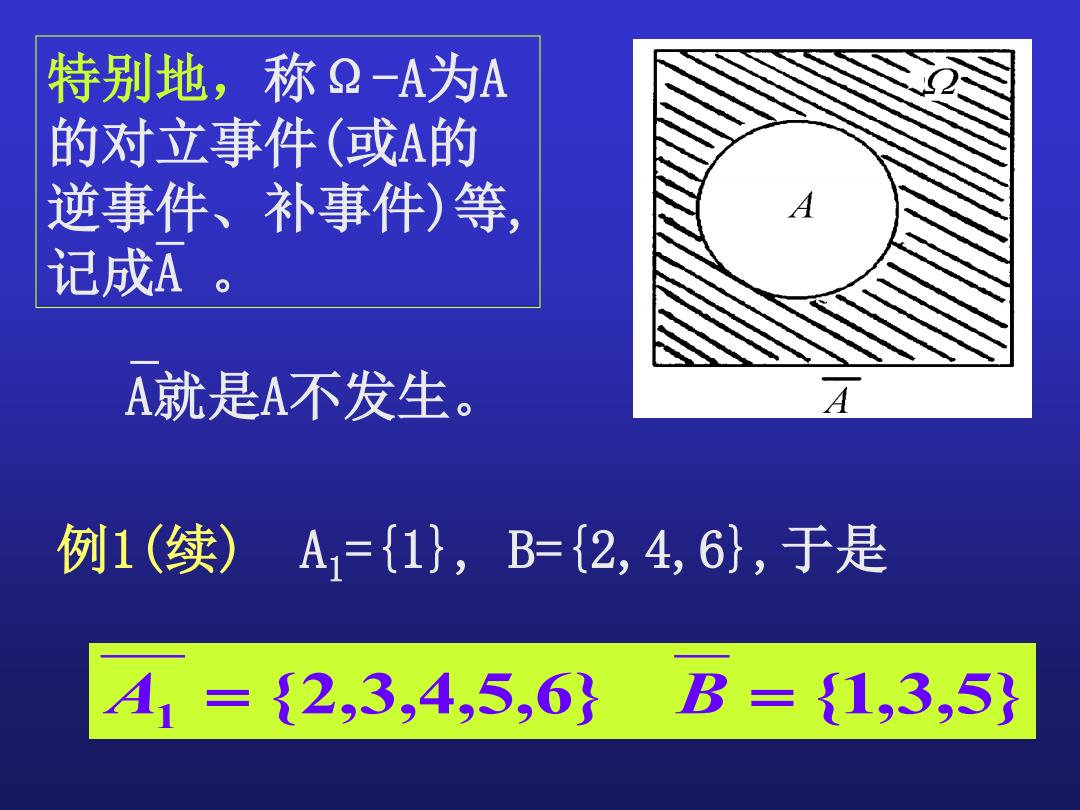
特别地,称Ω-A为A 的对立事件(或A的 逆事件、补事件)等, 记成A 。 例1(续) A1={1}, B={2,4,6},于是 A就是A不发生。 {2,3,4,5,6} {1,3,5} A1 = B =

II.事件的运算法则 (与集合运算法则相同) ◆交换律:AUB=BUA AB-BA ◆结合律:AU(BUC)=(AUB)UC A(BC)=(AB)C ◆分配律: ABUC)=ABUAC AU(BC)=(AUB)(AUC) ◆对偶律:AUB=AB AB-AUB 不是A,B中至少 A,B都不发生 有一个发生 还有常用 A-B=AB A=ABUAB
交换律: A∪B=B∪A AB=BA 结合律: A∪(B∪C)=(A∪B)∪C A(BC)=(AB)C 分配律: A(B∪C)=AB∪AC A∪(BC)=(A∪B)(A∪C) 对偶律: II. 事件的运算法则 (与集合运算法则相同) A B = AB AB = A B 还有常用 A − B = AB A = AB AB 不是A,B中至少 有一个发生 A,B都不发生

对于多个随机事件,上述运算规则也成立 A(AUA2U…UAn) =(AA)U(AA)UU(AA.) A1UA2UUAn=A,A,…A AA2…An=A1UA2U…UAn
对于多个随机事件,上述运算规则也成立 A(A1∪A2∪…∪An) =(AA1)∪(AA2)∪…∪(AAn) n n n n A A A A A A A A A A A A 1 2 1 2 1 2 1 2 = =

小结 本节首先介绍了随机试验、样本 空间的基本概念,然后给出了随机 事件的各种运算及运算法则
小结 本节首先介绍了随机试验、样本 空间的基本概念,然后给出了随机 事件的各种运算及运算法则

第一章第二节 事件的桡率
第一章第二节 事 件 的 概 率