
2、变量的显著性检验失去意义 在变量的显著性稔验中,统计量是建立在参 数方差正确估计基础之上的,这只有当随机误 差项具有同方差性和互相独立性时才能成立。 如果存在序列相关,估计的参数方差S 出现偏误(偏大或偏小),t检验就失去意义。 其他检验也是如此。 16
16 2、变量的显著性检验失去意义 在变量的显著性检验中,统计量是建立在参 数方差正确估计基础之上的,这只有当随机误 差项具有同方差性和互相独立性时才能成立。 其他检验也是如此

3、漠型的预测失效 区间预测与参数估计量的方差有关,在方 差有偏误的情况下,使得预测估计不准确,预 测精度降低。 所以,当模型出现序列相关性时,它的预 测功能失效。 17
17 3、模型的预测失效 区间预测与参数估计量的方差有关,在方 差有偏误的情况下,使得预测估计不准确,预 测精度降低。 所以,当模型出现序列相关性时,它的预 测功能失效

三、序列相关性的检验 基本思路: 序列相关性检验方法有多种,但基本思路相同: 首先,采用OLS法估计模型,以求得随机误差项的 “近似估计量”,用e,表示: @=Y,-(Y;)ons 然后,通过分析这些“近似估计量”之间的相 关性,以判断随机误差项是否具有序列相关性。 18
18 然后,通过分析这些“近似估计量”之间的相 关性,以判断随机误差项是否具有序列相关性。 序列相关性检验方法有多种,但基本思路相同: 首先,采用 OLS 法估计模型,以求得随机误差项的 “近似估计量”,用~ei表示: i Yi Yi l s e 0 ) ˆ ( ~ = − 基本思路: 三、序列相关性的检验
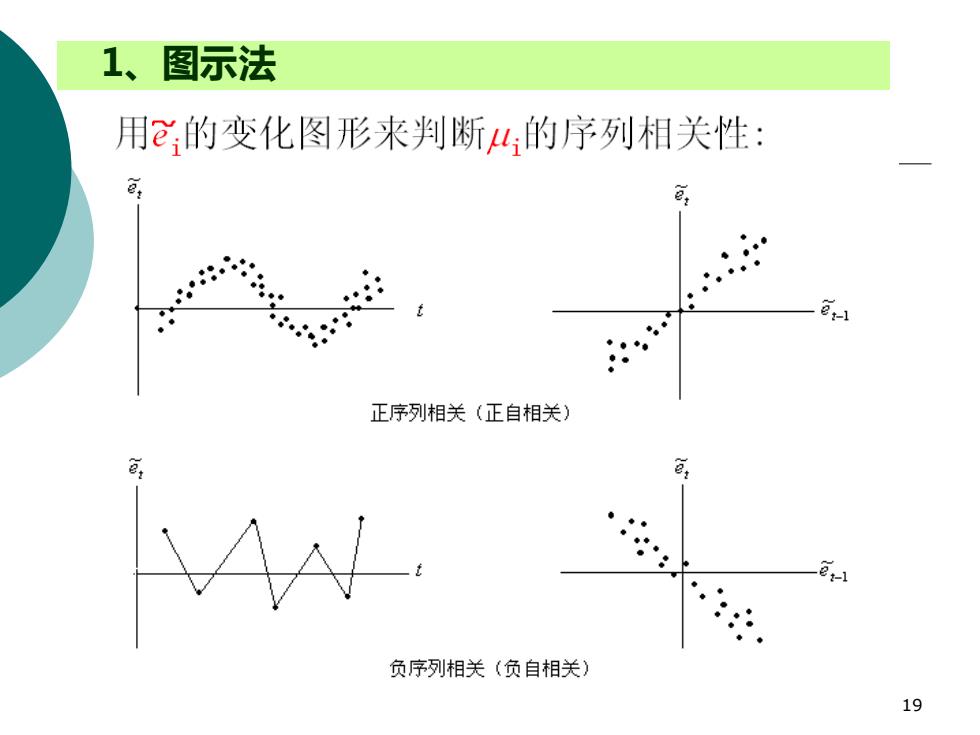
1、图示法 用E:的变化图形来判断4的序列相关性: 正序列相关(正自相关) 克 负序列相关(负自相关) 19
19 1、图示法

2、回归检验法 以,为被解释变量,以各种可能的相关量,诸如以e,-1、 ,-2、,等为解释变量,建立各种方程: e,=pe,-1+8, ,=pe+P2e-2+8, 如果存在某一种函数形式,使得方程显著成 立,则说明原模型存在序列相关性。 回归检验法的优点是:(1)首 能够确定序列相 关的形式,(2)适用于任何类型序列相关性问 题的检验。 20
20 2、回归检验法 以 t e ~ 为被解释变量,以各种可能的相关量,诸如以 1 ~ t− e 、 2 ~ t− e 、 ~2 t e 等为解释变量,建立各种方程: t t t e = e + −1 ~ ~ t t t t e = e + e + 1 −1 2 −2 ~ ~ ~ . 如果存在某一种函数形式,使得方程显著成 立,则说明原模型存在序列相关性。 回归检验法的优点是:(1)能够确定序列相 关的形式,(2)适用于任何类型序列相关性问 题的检验