
§4.4投资函数 (Investment Function) 加速模型 利润决定的投资函数模型 新古典投资函数模型 一个中国的投资函数模型
§4.4投资函数 (Investment Function) ❖加速模型 ❖利润决定的投资函数模型 ❖新古典投资函数模型 ❖一个中国的投资函数模型

一、加速模型
一、加速模型

1.常见4类模型形式 ·I、Y、K分别表示投资、国民收入、固定资产。 I,=f(△Y)+4 I,=f(Y,K,-1)+4 I=f(Y,Y-1,I-1)+4 I,=f(△Y,Y,-1,I,-1)+4 ÷分别为后面4类加速模型
⒈ 常见4类模型形式 ❖ 分别为后面4类加速模型。 I t = f Yt + t ( ) I t = f Yt Kt− + t ( , ) 1 I f Y Y I t = t t− t− + t ( , , ) 1 1 I f Y Y I t = t t− t− + t ( , , ) 1 1 • I、Y、K分别表示投资、国民收入、固定资产
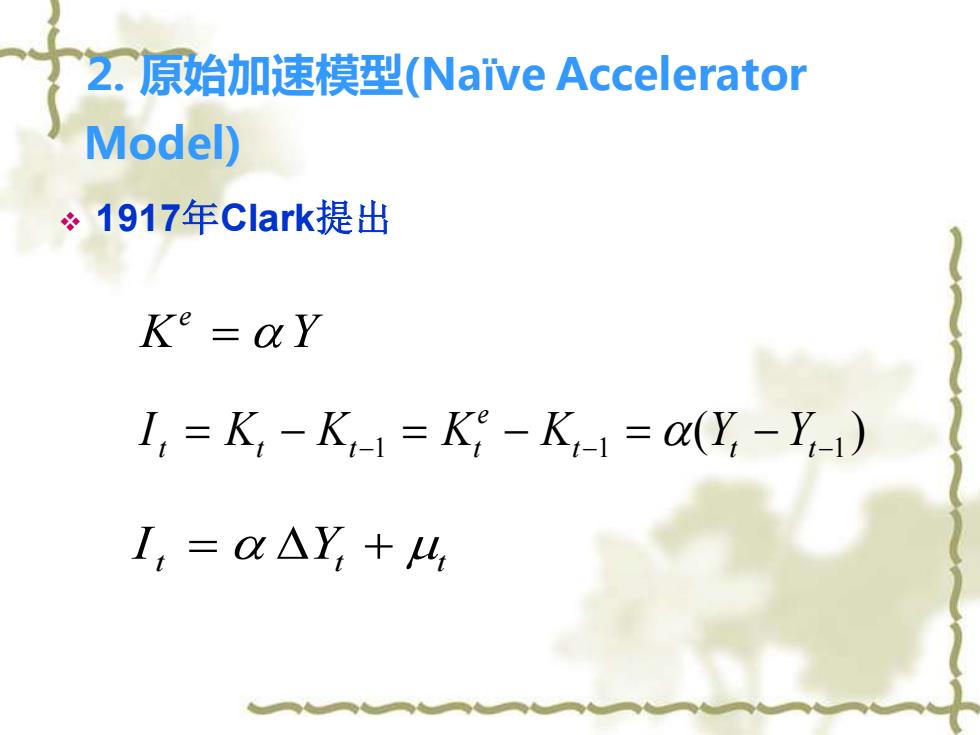
2.原始加速模型(Naive Accelerator Model) ÷1917年Clark提出 Ke=aY I,=K,-K-1=K-K-1=a(Y-Y-1)) I,=O△Y,+4
⒉ 原始加速模型(Naïve Accelerator Model) ❖ 1917年Clark提出 K Y e = I t Kt Kt Kt K Y Y e = − −1 = − t−1 = t − t−1 ( ) I t = Yt + t

3.灵活的加速模型(Flexible Accelerator Model Koyck于1954年 K-K,-1=元(K-K-1) K=2K+(1-2)K-1=九aY,+(1-)K,- K,=a(2Y,+元(1-2)Y1+元(1-元)2y-2+.) ·如果考虑到折旧,则有: I,=K,-K1+6K-1=u元Y+(6-)K,-1 I,=o2Y+(6-九)K,-1+4
⒊ 灵活的加速模型(Flexible Accelerator Model) ❖ Koyck于1954年 Kt Kt Kt K e − −1 = − t−1 ( ) Kt Kt K Y K e = + − t− = t + − t− (1 ) (1 ) 1 1 Kt = (Yt + (1− )Yt− + (1− ) Yt− + ) 1 2 2 I t = Kt − Kt−1 + Kt−1 = Yt + − Kt−1 ( ) I t = Yt + − Kt− + t ( ) 1 • 如果考虑到折旧,则有: