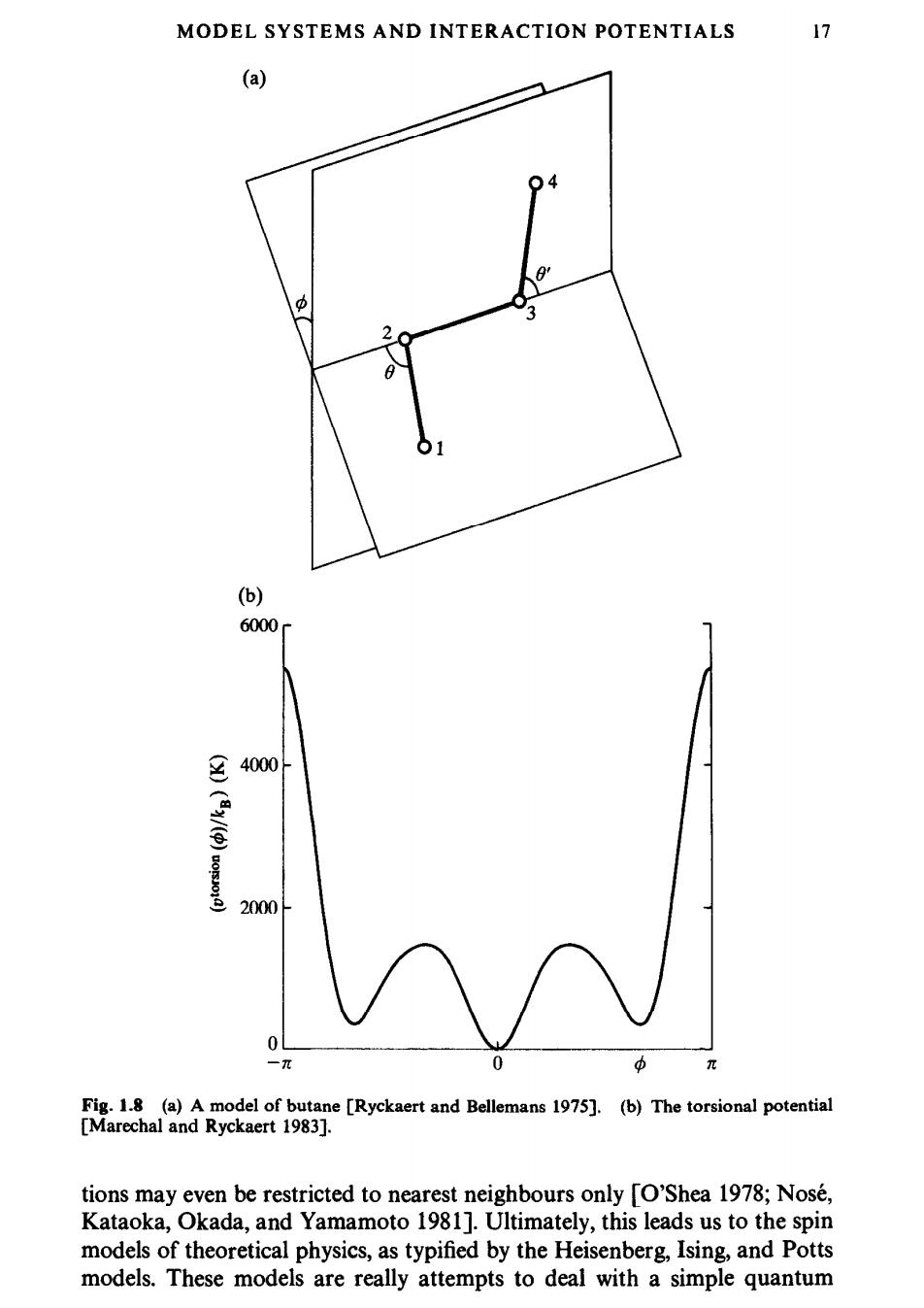
MODEL SYSTEMS AND INTERACTION POTENTIALS 17 (a) 04 中 3 2 01 (b) 6000 4000 2000 0 -n 中 π Fig.1.8 (a)A model of butane [Ryckaert and Bellemans 1975].(b)The torsional potential [Marechal and Ryckaert 1983]. tions may even be restricted to nearest neighbours only [O'Shea 1978;Nose, Kataoka,Okada,and Yamamoto 1981].Ultimately,this leads us to the spin models of theoretical physics,as typified by the Heisenberg,Ising,and Potts models.These models are really attempts to deal with a simple quantum

18 INTRODUCTION mechanical Hamiltonian for a solid-state lattice system,rather than the classical equations of motion for a liquid.However,because of its correspon- dence with the lattice gas model,the Ising model is still of some interest in classical liquid state theory.There has been a substantial amount of work involving Monte Carlo simulation of such spin systems,which we must regrettably omit from a book of this size.The importance of these idealized models in statistical mechanics is illustrated elsewhere [see e.g.Binder 1984, 1986;Toda,Kubo,and Saito 1983].Lattice model simulations,however,have been useful in the study of polymer chains,and we discuss this briefly in Chapter 4.Paradoxically,lattice models have also been useful in the study of liquid crystals,which we mention in Chapter 11. 1.3.5 Caicuiating the potential This is an appropriate point to introduce our first piece of computer code, which illustrates the calculation of the potential energy in a system of Lennard-Jones atoms.Converting the algebraic equations of this chapter into a form suitable for the computer is a straightforward exercise in FORmula TRANslation,for which the FORTRAN programming language has histori- cally been regarded as most suitable (see Appendix A).We suppose that the coordinate vectors of our atoms are stored in three FORTRAN arrays RX(I), RY(I)and RZ(I),with the particle index I varying from 1 to N(the number of particles).For the Lennard-Jones potential it is useful to have precomputed the value of o2,which is stored in the variable SIGSQ.The potential energy will be stored in a variable V,which is zeroed initially,and is then accumulated in a double loop over all distinct pairs of atoms,taking care to count each pair only once. Vm0.0 D0100I=1,N-1 RXI RX(I) RYI =RY(I) RZI RZ(I) D099J=I+1,N RXIJ RXI·RX(J) RYIJ=RYI·RY(J) RZIJ RZI·RZ(J) RIJSQ RXIJ *2 RYIJ 2 RZIJ *2 SR2 SIGSQ RIJSQ SR6 SR2SR2 SR2 SR12=SR6**2 小 =V+SR12·SR6 99 CONTINUE 100 CONTINUE V=4.0 EPSLON V

MODEL SYSTEMS AND INTERACTION POTENTIALS 19 Some measures have been taken here to avoid unnecessary use of computer time.The factor 4s (4.0 *EPSLON in FORTRAN),which appears in every pair potential term,is multiplied in once,at the very end,rather than many times within the crucial 'inner loop'over index J.We have used temporary variables RXI,RYI,and RZI so that we do not have to make a large number of array references in this inner loop.Other,more subtle points(such as whether it may be faster to compute the square of a number by using the exponen- tiation operation **or by multiplying the number by itself)are discussed in Appendix A.The more general questions of time-saving tricks in this part of the program are addressed in Chapter 5.The extension of this type of double loop to deal with other forms of the pair potential,and to compute forces in addition to potential terms,is straightforward,and examples will be given in later chapters.For molecular systems,the same general principles apply,but additional loops over the different sites or atoms in a molecule may be needed. For example,consider the site-site diatomic model of eqn(1.12)and Fig.1.6.If the coordinates of site a in molecule i are stored in array elements RX(I,A), RY(I,A),RZ(I,A),then the intermolecular interactions might be computed as follows: D0100A=1,2 D099B1,2 D098I1,N-1 D097J=I+1,N RXAB RX(I,A)-RX(J,B) RYAB RY(I,A)-RY(J,B) RZAB RZ(I,A)-RZ(J,B) calculate ia-jb interaction .. 97 CONTINUE 98 CONTINUE 99 CONTINUE 100 CONTINUE This use of doubly dimensioned arrays may not be efficient on some machines,but is quite convenient.Note that,apart from the dependence of the loop over J on the index I,the order of nesting is a matter of choice.Here,we have placed a loop over molecular indices innermost;assuming that N is relatively large,the vectorization of this loop on a pipeline machine will result in a great increase in speed of execution.Simulations of molecular systems may also involve the calculation of intramolecular energies,which,for site-site potentials,will necessitate a triple summation (over I,A,and B)

20 INTRODUCTION The above examples are essentially summations over pairs of interaction sites in the system.Any calculation of three-body interactions will,of course, entail triple summations of the kind D0100I=1,N-2 D099J=I+1,N-1 D098K=J+1,N ..calculate i-j-k interaction .. 98 CONTINUE 99 CONTINUE 100 CONTINUE Because all distinct triplets are examined,this will be much more time consuming than the summations described above.Even for pairwise- additive potentials,the energy or force calculation is the most expensive part of a computer simulation.We will return to this crucial section of the program in Chapter 5. 1.4 Constructing an intermolecular potential 1.4.1 Introduction There are essentially two stages in setting up a realistic simulation of a given system.The first is 'getting started'by constructing a first guess at a potential model.This should be a reasonable model of the system,and allow some preliminary simulations to be carried out.The second is to use the simulation results to refine the potential model in a systematic way,repeating the process several times if necessary.We consider the two phases in turn. 1.4.2 Building the model potential To illustrate the process of building up an intermo!ecular potential,we begin by considering a small molecule,such as N2,OCS,or CH4,which can be modelled using the interaction site potentials discussed in Section 1.3.The essential features of this model will be an anisotropic repulsive core,to represent the shape,an anisotropic dispersion interaction,and some partial charges to model the permanent electrostatic effects.This crude effective pair potential can then be refined by using it to calculate properties of the gas, liquid,and solid,and comparing with experiment. Each short-range site-site interaction can be modelled using a Lennard-Jones potential.Suitable energy and length parameters for interac-

CONSTRUCTING AN INTERMOLECULAR POTENTIAL 21 tions between pairs of identical atoms in different molecules are available from a number of simulation studies.Some of these are given in Table 1.1. Table 1.1.Atom-atom interaction parameters Atom Source e/kB(K) o(nm) H [Murad and Gubbins 1978] 8.6 0.281 He [Maitland et al.1981] 10.2 0.228 C [Tildesley and Madden 1981] 51.2 0.335 N [Cheung and Powles 1975] 37.3 0.331 0 [English and Venables 1974] 61.6 0.295 F [Singer et al.1977] 52.8 0.283 Ne [Maitland et al.1981] 47.0 0.272 S [Tildesley and Madden,1981] 183.0 0.352 CI [Singer et al.1977] 173.5 0.335 Ar [Maitland et al.1981] 119.8 0.341 Br [Singer et al.1977] 257.2 0.354 Kr [Maitland et al.1981] 164.0 0.383 The energy parameter e increases with atomic number as the polarizability goes up;o also increases down a group of the periodic table,but decreases from left to right across a period with the increasing nuclear charge.For elements which do not appear in Table 1.1,a guide to and o might be provided by the polarizability and van der Waals radius respectively.These values are only intended as a reasonable first guess:they take no regard of chemical environment and are not designed to be transferable.For example,the carbon atom parameters in CS2 given in the table are quite different from the values appropriate to a carbon atom in graphite [Crowell 1958].Interactions between unlike atoms in different molecules can be approximated using the venerable Lorentz-Berthelot mixing rules.For example,in CS2 the cross terms are given by Ocs =i[occ+ss] (1.18) and ecs=[eccess]112. (1.19) In tackling larger molecules,it may be necessary to model several atoms as a unified site.We have seen this for butane in Section 1.3,and a similar approach has been used in a model of benzene [Evans and Watts 1976].There are also complete sets of transferable potential parameters available for aromatic and aliphatic hydrocarbons [Williams 1965,1967],and for hydrogen-bonded liquids [Jorgensen 1981],which use the site-site approach.In the case of the Williams potentials,an exponential repulsion rather than Lennard-Jones power law is used.The specification of an interaction site model is made