
12 INTRODUCTION For ionic systems,induction interactions are important:the ionic charge induces a dipole on a neighbouring ion.This term is not pairwise additive and hence is difficult to include in a simulation.The shell model is a crude attempt to take this ion polarizability into account [Dixon and Sangster 1976].Each ion is represented as a core surrounded by a shell.Part of the ionic charge is located on the shell and the rest in the core.This division is always arranged so that the shell charge is negative (it represents the electronic cloud).The interactions between ions are just sums of the Coulombic shell-shell, core-core,and shell-core contributions.The shell and core of a given ion are coupled by a harmonic spring potential.The shells are taken to have zero mass. During a simulation,their positions are adjusted iteratively to zero the net force acting on each shell:this process makes the simulations very expensive. When a potential depends upon just a few parameters,such as eand o above, it may be possible to choose an appropriate set of units in which these parameters take values of unity.This results in a simpler description of the properties of the model,and there may also be technical advantages within a simulation program.For Coulomb systems,the factor 4neo in eqn (1.11)is often omitted,and this corresponds to choosing a non-standard unit of charge. We discuss such reduced units in Appendix B.Reduced densities,temperatures etc.are denoted by an asterisk,i.e.p*,T*etc. 1.3.3 Molecular systems In principle there is no reason to abandon the atomic approach when dealing with molecular systems:chemical bonds are simply interatomic potential energy terms [Chandler 1982].Ideally,we would like to treat all aspects of chemical bonding,including the reactions which form and break bonds,in a proper quantum mechanical fashion.This difficult task has not yet been accomplished.On the other hand,the classical approximation is likely to be seriously in error for intramolecular bonds.The most common solution to these problems is to treat the molecule as a rigid or semi-rigid,unit,with fixed bond lengths and,sometimes,fixed bond angles and torsion angles.The rationale here is that bond vibrations are of very high frequency(and hence difficult to handle,certainly in a classical simulation)but of low amplitude (therefore being unimportant for many liquid properties).Thus,a diatomic molecule with a strongly binding interatomic potential energy surface might be replaced by a dumb-bell with a rigid interatomic bond. The interaction between the nuclei and electronic charge clouds of a pair of molecules i and jis clearly a complicated function of relative positions ri,r and orientations i,j [Gray and Gubbins 1984].One way of modelling a molecule is to concentrate on the positions and sizes of the constituent atoms [Eyring 1932].The much simplified 'atom-atom'or'site-site'approximation for diatomic molecules is illustrated in Fig.1.6.The total interaction is a sum of

MODEL SYSTEMS AND INTERACTION POTENTIALS 13 Fig.1.6 An atom-atom model of a diatomic molecule. pairwise contributions from distinct sites a in molecule i,at position ri and b in molecule j,at position r v(ri,2》=∑∑Vab(Tab) (1.12) a b Here a,b take the values 1,2,vab is the pair potential acting between sites a and b,and rab is shorthand for the inter-site separation rab=lria-jbl. The interaction sites are usually centred,more or less,on the positions of the nuclei in the real molecule,so as to represent the basic effects of molecular 'shape'.A very simple extension of the hard-sphere model is to consider a diatomic composed of two hard spheres fused together [Streett and Tildesley 1976],but more realistic models involve continuous potentials.Thus, nitrogen,fluorine,chlorine etc.have been depicted as two Lennard-Jones atoms'separated by a fixed bond length [Barojas et al.1973;Cheung and Powles 1975;Singer,Taylor,and Singer 1977].Similar approaches apply to polyatomic molecules. The description of the molecular charge distribution may be improved somewhat by incorporating point multipole moments at the centre of charge [Streett and Tildesley 1977].These multipoles may be equal to the known (isolated molecule)values,or may be 'effective'values chosen simply to yield a better description of the liquid structure and thermodynamic properties.It is now generally accepted that such a multipole expansion is not rapidly convergent.A promising alternative approach for ionic and polar systems,is to use a set of fictitious partial charges'distributed 'in a physically reasonable way'around the molecule so as to reproduce the known multipole moments [Murthy,O'Shea,and McDonald 1983],and a further refinement is to
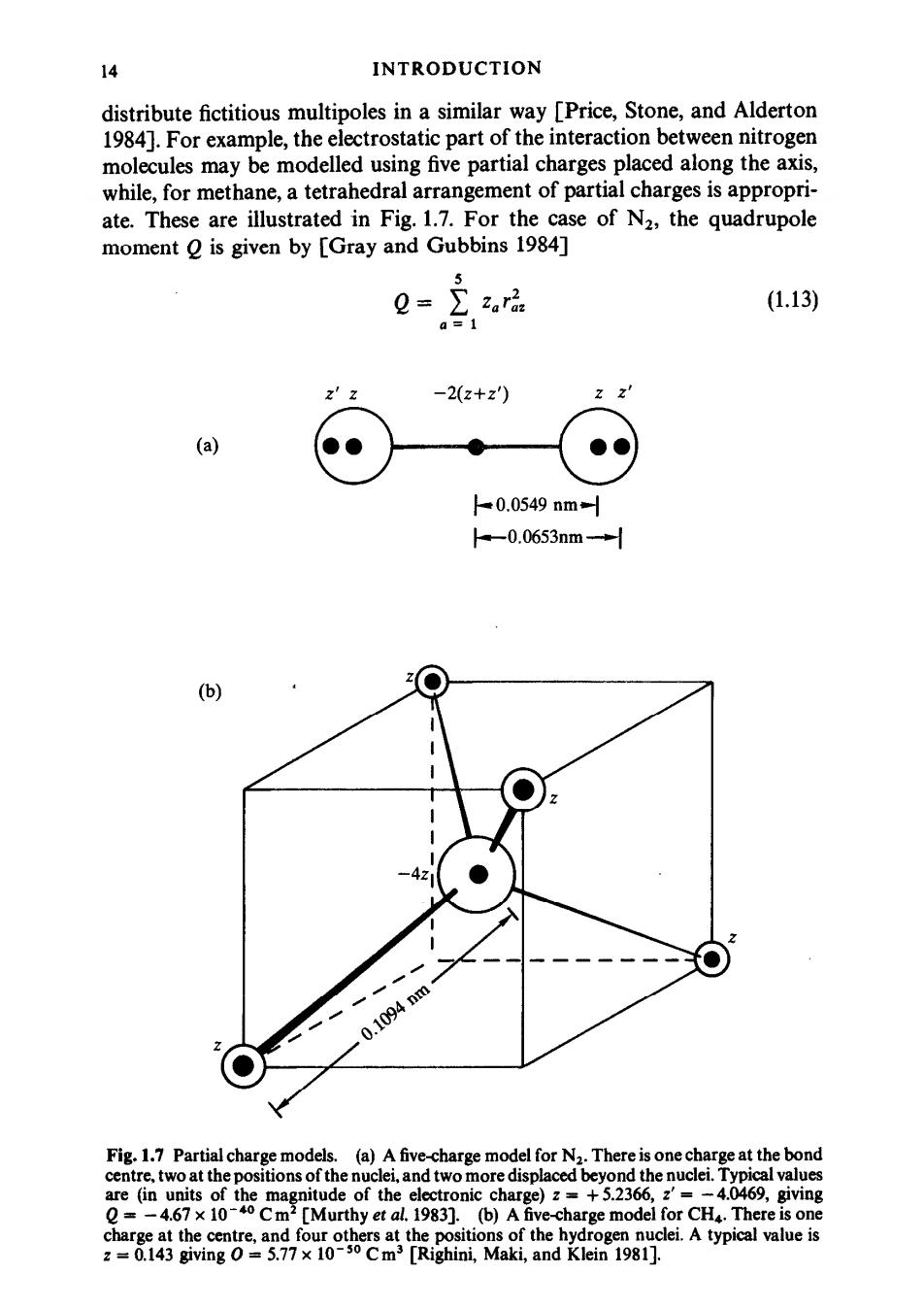
14 INTRODUCTION distribute fictitious multipoles in a similar way [Price,Stone,and Alderton 1984].For example,the electrostatic part of the interaction between nitrogen molecules may be modelled using five partial charges placed along the axis, while,for methane,a tetrahedral arrangement of partial charges is appropri- ate.These are illustrated in Fig.1.7.For the case of N2,the quadrupole moment Q is given by [Gray and Gubbins 1984] 5 =∑zra (1.13) a=1 2′z -2(z+z) (a) -0.0549nm= -0.0653nm-+ (b) 0.1094nm Fig.1.7 Partial charge models.(a)A five-charge model for N2.There is one charge at the bond centre,two at the positions of the nuclei,and two more displaced beyond the nuclei.Typical values are (in units of the magnitude of the electronic charge)z=+5.2366,z'=-4.0469,giving Q=-4.67 x 10-40 Cm2 [Murthy et al.1983].(b)A five-charge model for CH4.There is one charge at the centre,and four others at the positions of the hydrogen nuclei.A typical value is z=0.143 giving O=5.77x 10-30 Cm3 [Righini,Maki,and Klein 1981]

MODEL SYSTEMS AND INTERACTION POTENTIALS 15 with similar expressions for the higher multipoles(all the odd ones vanish for N2).The first non-vanishing moment for methane is the octopole 2.1 (1.14) in the coordinate system of Fig.1.7.The aim of all these approaches is to approximate the complete charge distribution in the molecule.In a calculation of the potential energy,the interaction between partial charges on different molecules would be summed in the same way as the other site-site interactions. For large rigid models,a substantial number of sites would be required to model the repulsive core.For example,a crude model of the nematogen quinquaphenyl,which represented each of the five benzene rings as a single Lennard-Jones site,would necessitate 25 site-site interactions between each pair of molecules;sites based on each carbon atom would be more realistic but extremely expensive.An alternative type of intermolecular potential,intro- duced by Corner [1948],involves a single site-site interaction between a pair of molecules,characterized by energy and length parameters that depend on the relative orientation of the molecules.A version of this family of molecular potentials that has been used in computer simulation studies is the Gaussian overlap model generalized to a Lennard-Jones form [Berne and Pechukas 1972].The basic potential acting between two linear molecules is the Lennard- Jones interaction,eqn(1.6),with the angular dependence of and o determined by considering the overlap of two ellipsoidal Gaussian functions(representing the electron clouds of the molecules).The energy parameter is written . e(2,n)=&ph(1-x2(e.e)2)1/2 (1.15) where eph is a constant and e,ej are unit vectors describing the orientation of the molecules iand j.x is an anisotropy parameter determined by the length of the major and minor axes of the electron cloud ellipsoid X=(σ2-σ12)/(op+o12). (1.16) The length parameter is given by an-[l- /2 +-x:6 (1.17) where osph is a constant.In certain respects,this form of the overlap potential is unrealistic,and it has been extended to make also dependent upon ry [Gay and Berne 1981].The extended potential can be parameterized to mimic a linear site-site potential,and should be particularly useful in the simulation of nematic liquid crystals

16 INTRODUCTION For larger molecules it may not be reasonable to 'fix'all the internal degrees of freedom.In particular,torsional motion about bonds,which gives rise to conformational interconversion in,for example,alkanes,cannot in general be neglected (since these motions involve energy changes comparable with normal thermal energies).An early simulation of n-butane,CH3CH2CH2CH3 [Ryckaert and Bellemans 1975;Marechal and Ryckaert 1983].providesa good example of the way in which these features are incorporated in a simple model. Butane can be represented as a four-centre molecule,with fixed bond lengths and bond bending angles,derived from known experimental(structural)data (see Fig.1.8).A very common simplifying feature is built into this model:whole groups of atoms,such as CH3 and CH2,are condensed into spherically symmetric effective 'united atoms'.In fact,for butane,the interactions between such groups may be represented quite well by the ubiquitous Lennard-Jones potential,with empirically chosen parameters.In a simulation,the Ci-C2, C2-C3 and C3-C4 bond lengths are held fixed by a method of constraints which will be described in detail in Chapter 3.The angles 0 and may be fixed by additionally constraining the C1-C3 and C2-C4 distances,i.e.by introduc- ing 'phantom bonds'.If this is done,just one internal degree of freedom, namely the rotation about the C2-C3 bond,measured by the angle is left unconstrained;for each molecule,an extra term in the potential energy, ()periodic in appears in the hamiltonian.This potential would have a minimum at a value of corresponding to the trans conformer of butane, and secondary minima at the gauche conformations.It is easy to see how this approach may be extended to much larger flexible molecules.The con- sequences of constraining bond lengths and angles will be treated in more detail in Chapters 2-4. As the molecular model becomes more complicated,so too do the expressions for the potential energy,forces,and torques,due to molecular interactions.In Appendix C,we give some examples of these formulae,for rigid and flexible molecules,interacting via site-site pairwise potentials, including multipolar terms.We also show how to derive the forces from a simple three-body potential. 1.3.4 Lattice systems We may also consider the consequences of removing rather than adding degrees of freedom to the molecular model.In a crystal,molecular translation is severely restricted,while rotational motion (in plastic crystals for instance) may still occur.A simplified model of this situation may be devised,in which the molecular centres of mass are fixed at their equilibrium crystal lattice sites, and the potential energy is written solely as a function of molecular orientations.Such models are frequently of theoretical,rather than practical, interest,and accordingly the interactions are often of a very idealized form:the molecules may be represented as point multipoles for example,and interac-