
MODEL SYSTEMS AND INTERACTION POTENTIALS 7 where m;is the molecular mass,and the index a runs over the different (x,y,z) components of the momentum of molecule i.The potential energy contains the interesting information regarding intermolecular interactions:assuming that is fairly sensibly behaved,it will be possible to construct,from an equation of motion(in Hamiltonian,Lagrangian,or Newtonian form)which governs the entire time-evolution of the system and all its mechanical properties [Goldstein 1980].Solution of this equation will generally involve calculating,from the forces fi,and torques i,acting on the molecules(see Chapter 3).The Hamiltonian also dictates the equilibrium distribution function for molecular positions and momenta (see Chapter 2).Thus, generally,it is(or)which is the basic input to a computer simulation program.The approach used almost universally in computer simulation is to break up the potential energy into terms involving pairs,triplets,etc.of molecules.In the following sections we shall consider this in detail. Before leaving this section,we should mention briefly somewhat different approaches to the calculation of.In these developments,the distribution of electrons in the system is not modelled by an effective potential(q),but is treated by a form of density functional theory.In one approach,the electron density is represented by an extension of the electron gas theory [LeSar and Gordon 1982,1983;LeSar 1984].In another,electronic degrees of freedom are explicitly included in the description,and the electrons are allowed to relax during the course of the simulation by a process known as 'simulated annealing'[Car and Parrinello 1985].Both these methods avoid the division of into pairwise and higher terms.They seem promising for future simulations of solids and liquids 1.3.2 Atomic systems Consider first the simple case of a system containing N atoms.The potential energy may be divided into terms depending on the coordinates of individual atoms,pairs,triplets etc.: 少=,e+E功+g品,W+… (1.4) i j>ik>j>i Thenotation indicates asummation over all distinct pairs iandjwithout ii>i counting any pair twice(i.e.as ijand ji);the same care must be taken for triplets etc.The first term in eqn(1.4),v(r:),represents the effect of an external field (including,for example,the container walls)on the system.The remaining terms represent particle interactions.The second term,v2,the pair potential,is the most important.The pair potential depends only on the magnitude of the pair separation rj=ri-rjl,so it may be written v2(r).Figure 1.3 shows one of the more recent estimates for the pair potential between two argon atoms,as
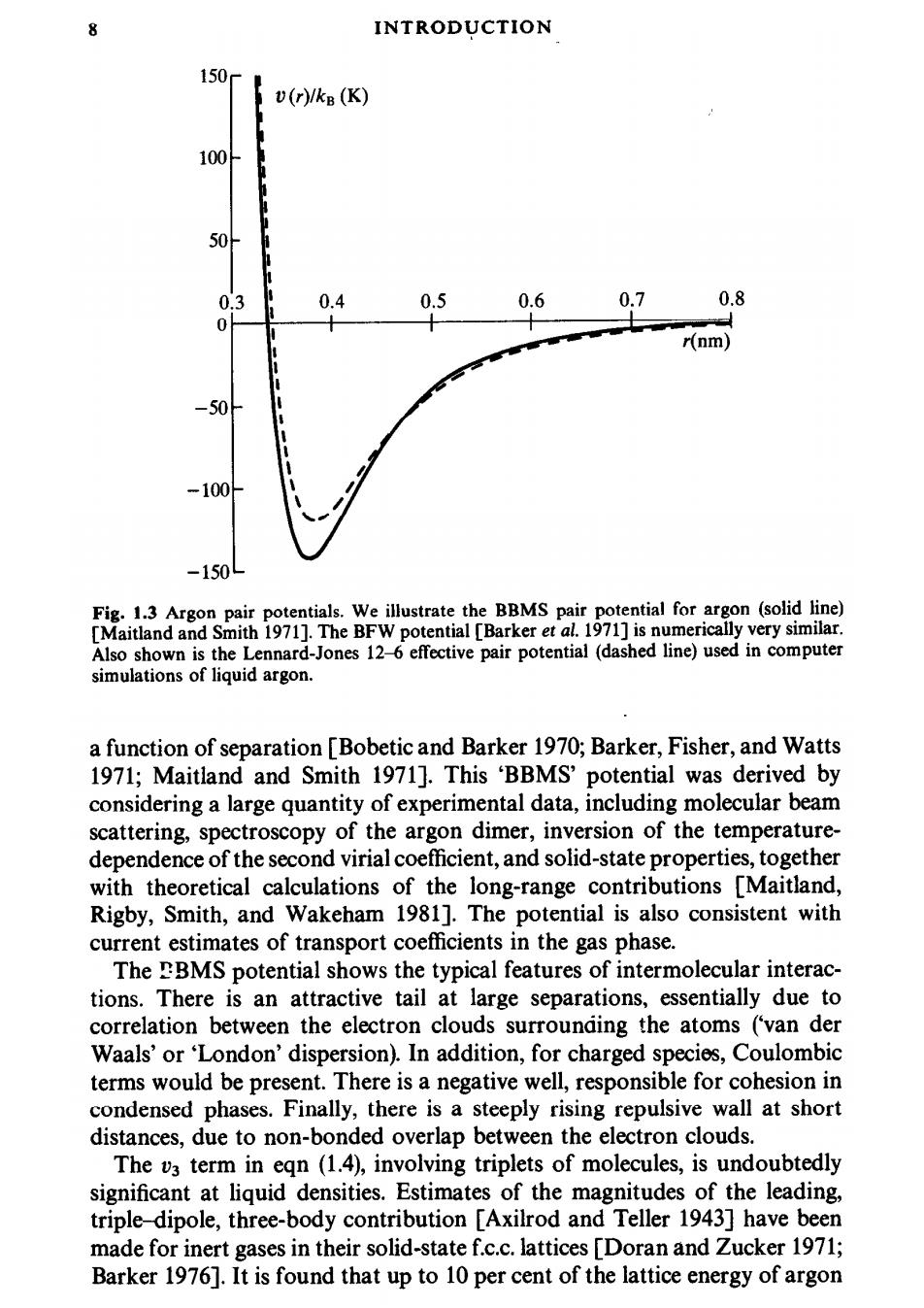
8 INTRODUCTION 50 v(r)/kB(K) 100 0.3 0.4 0.5 0.6 0.7 0.8 r(nm -150 Fig.1.3 Argon pair potentials.We illustrate the BBMS pair potential for argon (solid line) [Maitland and Smith 1971].The BFW potential [Barker et al.1971]is numerically very similar Also shown is the Lennard-Jones 12-6 effective pair potential (dashed line)used in computer simulations of liquid argon. a function of separation [Bobetic and Barker 1970;Barker,Fisher,and Watts 1971;Maitland and Smith 1971].This 'BBMS'potential was derived by considering a large quantity of experimental data,including molecular beam scattering,spectroscopy of the argon dimer,inversion of the temperature- dependence of the second virial coefficient,and solid-state properties,together with theoretical calculations of the long-range contributions [Maitland, Rigby,Smith,and Wakeham 1981].The potential is also consistent with current estimates of transport coefficients in the gas phase. The BMS potential shows the typical features of intermolecular interac- tions.There is an attractive tail at large separations,essentially due to correlation between the electron clouds surrounding the atoms ('van der Waals'or'London'dispersion).In addition,for charged species,Coulombic terms would be present.There is a negative well,responsible for cohesion in condensed phases.Finally,there is a steeply rising repulsive wall at short distances,due to non-bonded overlap between the electron clouds. The v3 term in eqn (1.4),involving triplets of molecules,is undoubtedly significant at liquid densities.Estimates of the magnitudes of the leading, triple-dipole,three-body contribution [Axilrod and Teller 1943]have been made for inert gases in their solid-state f.c.c.lattices [Doran and Zucker 1971; Barker 1976].It is found that up to 10 per cent of the lattice energy of argon

MODEL SYSTEMS AND INTERACTION POTENTIALS 9 (and more in the case of more polarizable species)may be due to these non- additive terms in the potential;we may expect the same order of magnitude to hold in the liquid phase.Four-body(and higher)terms in eqn(1.4)are expected to be small in comparison with vz and v3. Despite the size of three-body terms in the potential,they are only rarely included in computer simulations [Barker et al.1971;Monson,Rigby,and Steele 1983].This is because,as we shall see shortly,the calculation of any quantity involving a sum over triplets of molecules will be very time- consuming on a computer.Fortunately,the pairwise approximation gives a remarkably good description of liquid properties because the average three- body effects can be partially included by defining an 'effective'pair potential. To do this,we rewrite eqn (1.4)in the form 少≈,)+. (1.5) The pair potentials appearing in computer simulations are generally to be regarded as effective pair potentials of this kind,representing all the many- body effects;for simplicity,we will just use the notation (rij)or v(r).A consequence of this approximation is that the effective pair potential needed to reproduce experimental data may turn out to depend on the density, temperature etc.,while the true two-body potential v(rj)of course does not. Now we turn to the simpler,more idealized,pair potentials commonly used in computer simulations.These reflect the salient features of real interactions ina general,often empirical,way.Illustrated with the BBMS argon potential in Fig.1.3 is a simple Lennard-Jones 12-6 potential J(r)=4ε(o/r)12-(c/r)) (1.6) which provides a reasonable description of the properties of argon,via computer simulation,if the parameters e and o are chosen appropriately.The potential has a long-range attractive tail of the form-1/r6,a negative well of depth e,and a steeply rising repulsive wall at distances less than r~o.The well-depth is often quoted in units of temperature as e/kB,where kB is Boltzmann's constant;values of e/kB120 K and 0.34 nm provide reasonable agreement with the experimental properties of liquid argon.Once again,we must emphasize that these are not the values which would apply to an isolated pair of argon atoms,as is clear from Fig.1.3 For the purposes of investigating general properties of liquids,and for comparison with theory,highly idealized pair potentials may be of value.In Fig.1.4,we illustrate three forms which,although unrealistic,are very simple and convenient to use in computer simulation and in liquid-state theory.These are:the hard-sphere potential HS(r)= r<) 0 (o≤r) (1.7)
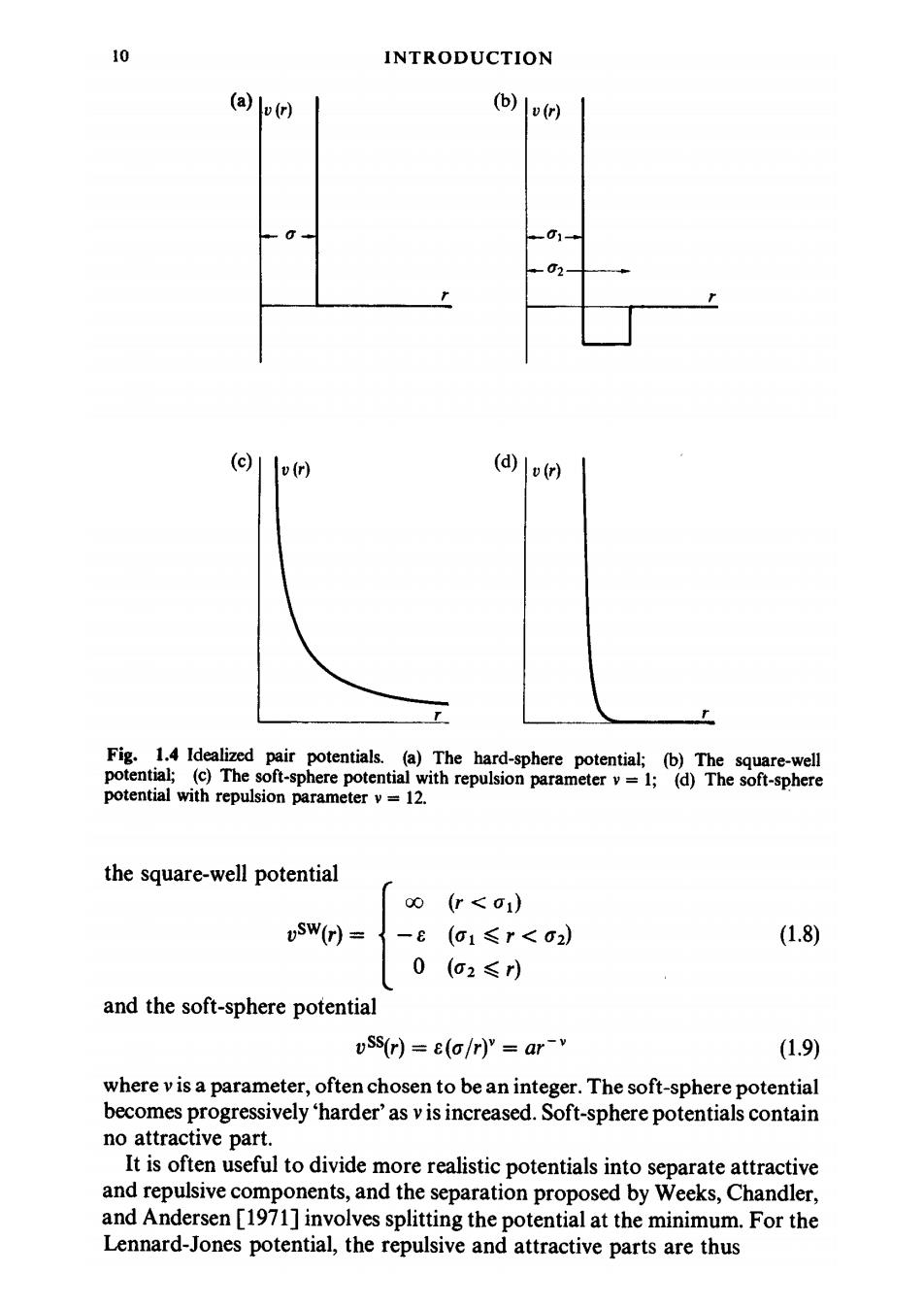
10 INTRODUCTION (a) v(r) (b)(r) -0 01- (c) v(r) (d) v(r) Fig.1.4 Idealized pair potentials.(a)The hard-sphere potential;(b)The square-well potential;(c)The soft-sphere potential with repulsion parameter v=1;(d)The soft-sphere potential with repulsion parameter v=12. the square-well potential 00 (r<o1) -E (a1≤r<o2) (1.8) 0 (o2≤) and the soft-sphere potential uSs(r)=e(a/r)"ar-v (1.9) where v is a parameter,often chosen to be an integer.The soft-sphere potential becomes progressively 'harder'as v is increased.Soft-sphere potentials contain no attractive part. It is often useful to divide more realistic potentials into separate attractive and repulsive components,and the separation proposed by Weeks,Chandler, and Andersen [1971]involves splitting the potential at the minimum.For the Lennard-Jones potential,the repulsive and attractive parts are thus
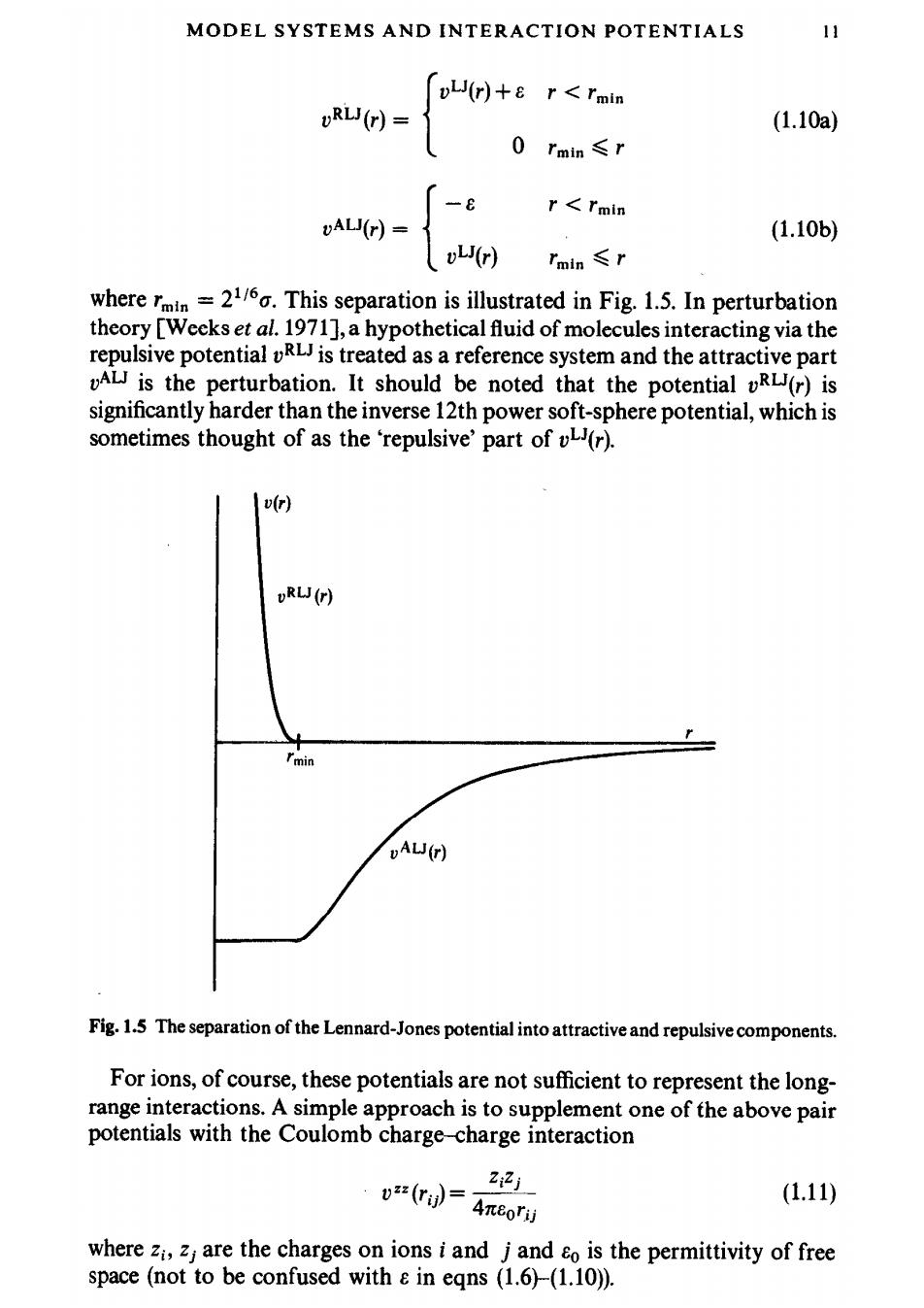
MODEL SYSTEMS AND INTERACTION POTENTIALS 11 L(r)+8 r<rmin oRL(r)- (1.10a) 0 rmin≤r -{ r<Imin (1.106) Tmin≤r wherem.This separation is illustrated in Fig.1.5.In perturbation theory [Weeks et al.1971],a hypothetical fluid of molecules interacting via the repulsive potential uR is treated as a reference system and the attractive part AL is the perturbation.It should be noted that the potential R(r)is significantly harder than the inverse 12th power soft-sphere potential,which is sometimes thought of as the 'repulsive'part of (r). v(r) oRLJ(r) DALJ(r) Fig.1.5 The separation of the Lennard-Jones potential into attractive and repulsive components. For ions,of course,these potentials are not sufficient to represent the long- range interactions.A simple approach is to supplement one of the above pair potentials with the Coulomb charge-charge interaction 66品 (1.11) where zi,zj are the charges on ions i and j and &o is the permittivity of free space (not to be confused with in eqns (1.6)-(1.10))