
第三章平面机构的运动分析 内容提要 本章主要介绍机构运动分析的目的和方法,重点介绍了三种机构运动分析方法,即重点介绍 了三种机构运动分析方法,即速度瞬心法、相对运动图解法和解析法。 3.1机构运动分析的目的和方法 3.1.1机构运动分析的目的 机构运动分析是在不考虑外力的作用和构件的弹性变形,以及运动副间隙对机构运动影响的 情况下,根据己知机构的运动简图和原动件的运动规律,求解机构中其他构件的位移(角位移)、 速度(角速度)和加速度(角加速度)等运动参数。机构的运动分析是了解机械的运动性能的依 据,对正确地了解与应用机构的运动性能和校核所设计的机构是否满足设计要求有重要的作用。 3.1.2机构运动分析的方法 机构运动分析的方法主要有图解法和解析法,图解法又分为相对运动图解法和速度瞬心法, 图解法对简单的平面机构设计具有形象、直观、图解过程简单易行等特点,是运动分析的基本方 法,但精度不高,而且对机构的一系列位置进行分析时,需反复作图而显得繁琐。解析法需根据 机构中的已知参数建立数学模型,然后借助计算机进行求解,它不仅可方便地对机构进行一个运 动循环过程的研究,而且还便于把机构分析和综合问题联系起米,以求得最优方案。由于解析法 具有较高的精度,现在被广泛使用。本章将对上述两种方法在平面机构运动分析中的运用分别加 以介绍。 3.2用速度瞬心法对机构进行速度分析 3.2.1速度瞬心及机构中速度瞬心的数目 作平面相对运动的两构件,在任一瞬时位置其相对运动均可看作是绕某一重合点的相对转 动。该重合点即为相对转动中心,称为速度解心(instantaneous center of velocity),简称瞬心
28 第三章 平面机构的运动分析 内容提要 本章主要介绍机构运动分析的目的和方法,重点介绍了三种机构运动分析方法,即重点介绍 了三种机构运动分析方法,即速度瞬心法、相对运动图解法和解析法。 3.1 机构运动分析的目的和方法 3.1.1 机构运动分析的目的 机构运动分析是在不考虑外力的作用和构件的弹性变形,以及运动副间隙对机构运动影响的 情况下,根据已知机构的运动简图和原动件的运动规律,求解机构中其他构件的位移(角位移)、 速度(角速度)和加速度(角加速度)等运动参数。机构的运动分析是了解机械的运动性能的依 据,对正确地了解与应用机构的运动性能和校核所设计的机构是否满足设计要求有重要的作用。 3.1.2 机构运动分析的方法 机构运动分析的方法主要有图解法和解析法,图解法又分为相对运动图解法和速度瞬心法。 图解法对简单的平面机构设计具有形象、直观、图解过程简单易行等特点,是运动分析的基本方 法,但精度不高,而且对机构的一系列位置进行分析时,需反复作图而显得繁琐。解析法需根据 机构中的已知参数建立数学模型,然后借助计算机进行求解,它不仅可方便地对机构进行一个运 动循环过程的研究,而且还便于把机构分析和综合问题联系起来,以求得最优方案。由于解析法 具有较高的精度,现在被广泛使用。本章将对上述两种方法在平面机构运动分析中的运用分别加 以介绍。 3.2 用速度瞬心法对机构进行速度分析 3.2.1 速度瞬心及机构中速度瞬心的数目 作平面相对运动的两构件,在任一瞬时位置其相对运动均可看作是绕某一重合点的相对转 动。该重合点即为相对转动中心,称为速度瞬心(instantaneous center of velocity),简称瞬心

构件人、了之间的瞬心用符号P表示。因此,两构件在瞬心点处的相对速度为零,其绝对速度相 等。若瞬心的绝对速度为零,则称为绝对瞬心(absolute instantaneous center),运动构件与机架 之间的瞬心即为绝对瞬心。若瞬心的绝对速度不为零,则称为相对瞬心,两运动构件之间的瞬心 即为相对瞬心(relative instantaneous center)。因为机构中每两个构件间就有一个瞬心,所以有N 个构件组成的机构,其总的瞬心数K为 K=N(W-1) 2 (3-1) 3.2.2机构中速度瞬心的确定 1.通过运动副直接相连的两构件间的瞬心 通过运动副直接相连的两构件间的瞬心可以通过直接观察即可确定。 (1)以转动副相连接的两构件的瞬心在转动副的中心处。如图3-1a所示的构件1和构件2 的瞬心B2就在两构件的转动副的中心处。 (2)以移动副相连接的两构件间的瞬心位于垂直于导路方向的无穷远处,如图3-1b所示的 P2位于垂直于构件1和构件2所构成的移动副导路方向的无穷远处。 (3)以平面高副相连接的两构件间的瞬心,当高副两元素作纯滚动时就在接触点处,如图 31c所示的P,即为构件1和构件2的接触点M:当高副两元素间有相对滑动时,则在过接触点 两高副元素的公法线上,如图3-1d所示的构件1和构件2之间存在相对滑动速度1e,则二者 的瞬心就位于法线-?上。不过因为滚动和滑动的数值尚不知,所以还不能确定它是在法线上的 那一点。 (a) (b) (c) (o) 图3-1观察法确定速度瞬心 2.不直接相连的两构件的瞬心 不直接相连的两构件间的瞬心位置,可借助三心定理来确定.所谓三心定理(Kennedy-Around theorem),即三个彼此作平面云动的构件的三个舞心必位于同一直线上。如图3.2所示构件1、2、 3彼此作相对平面运动,它们之间共有三个瞬心D2、P3、P:。其中P:、P23分别在构件1、3 和2、3之间转动副的转动中心O、O2处,而不直接通过运动副相连的两构件1、2之间的瞬心 P2必位于P;、P23的连线上。 有了直接观察法和三心定理便可确定机构的全部瞬心位置。但对多杆机构,构件越多,瞬心 数目就越多,求解不大方便。为此,下面提出用解心多边形和上述两种方法相结合来求取瞬心
29 构件 i、j 之间的瞬心用符号 Pij 表示。因此,两构件在瞬心点处的相对速度为零,其绝对速度相 等。若瞬心的绝对速度为零,则称为绝对瞬心(absolute instantaneous center),运动构件与机架 之间的瞬心即为绝对瞬心。若瞬心的绝对速度不为零,则称为相对瞬心,两运动构件之间的瞬心 即为相对瞬心(relative instantaneous center)。因为机构中每两个构件间就有一个瞬心,所以有 N 个构件组成的机构,其总的瞬心数 K 为 2 ( −1) = N N K (3-1) 3.2.2 机构中速度瞬心的确定 1.通过运动副直接相连的两构件间的瞬心 通过运动副直接相连的两构件间的瞬心可以通过直接观察即可确定。 (1)以转动副相连接的两构件的瞬心在转动副的中心处。如图 3-1a 所示的构件 1 和构件 2 的瞬心 P12 就在两构件的转动副的中心处。 (2)以移动副相连接的两构件间的瞬心位于垂直于导路方向的无穷远处,如图 3-1b 所示的 P12 位于垂直于构件 1 和构件 2 所构成的移动副导路方向的无穷远处。 (3)以平面高副相连接的两构件间的瞬心,当高副两元素作纯滚动时就在接触点处,如图 3-1c 所示的 P12 即为构件 1 和构件 2 的接触点 M ;当高副两元素间有相对滑动时,则在过接触点 两高副元素的公法线上,如图 3-1d 所示的构件 1 和构件 2 之间存在相对滑动速度 M1M2 v ,则二者 的瞬心就位于法线 n-n 上。不过因为滚动和滑动的数值尚不知,所以还不能确定它是在法线上的 那一点。 (a) (b) (c) (d) 图 3-1 观察法确定速度瞬心 2.不直接相连的两构件的瞬心 不直接相连的两构件间的瞬心位置,可借助三心定理来确定。所谓三心定理(Kennedy-Around theorem),即三个彼此作平面运动的构件的三个瞬心必位于同一直线上。如图 3-2 所示构件 l、2、 3 彼此作相对平面运动,它们之间共有三个瞬心 P12 、 P23 、P13 。其中 P13 、 P23 分别在构件 1、3 和 2、3 之间转动副的转动中心 O1 、O2 处,而不直接通过运动副相连的两构件 1、2 之间的瞬心 P12 必位于 P13 、 P23 的连线上。 有了直接观察法和三心定理便可确定机构的全部瞬心位置。但对多杆机构,构件越多,瞬心 数目就越多,求解不大方便。为此,下面提出用瞬心多边形和上述两种方法相结合来求取瞬心
具体求法如下: (R) 为=当 77777777777777777 图32三心定理 (1)先画一个圆,然后按照机构的构件数分割该圆,并在分割点上依次(顺时针或逆时针) 标注构件号。 (2)通过直接观察法求瞬心。将能直接观察求出瞬心位置的两构件的分割点用实线相连, 则此实线即代表己知的该两构件间的瞬心。 (3)观察在圆中尚未连线的分割点,将能连成两个三角形的公共边的点用虚线连接,则此 虚线就代表可求取的未知瞬心。 (4)在有公共边的两个三角形中,每个三角形的3条边代表3个构件的3个瞬心。根据三 心定理,这3个瞬心必在同一直线上。现在三角形除公共虚边以外的另外两个边代表的2个瞬心 己知,在机构图上用直线连接这两个边代表的己知瞬心,则公共虚边代表的未知瞬心必定位于这 一直线上。这样,两个三角形的各个已知两边代表的两个已知瞬心共作出2条直线,2条直线的 交点就是公共虚边代表的未知瞬心。 (5)确定公共虚边代表的未知瞬心后,公共虚边可画成实边,重复前述步骤,可以确定其 他待求的未知瞬心。 【例31】如图33所示为一较链四杆机构,试确定该机构全部瞬心的位置。 P (a) (b) 图33铰链四杆机构瞬心的确定 解:该机构瞬心的数目为K=N-山_44-D=6,分别为、、、P、、 2 2 P4。其中,直接观察可得到瞬心P2、P、P4、P4分别在转动副A、B、C、D的回转中心
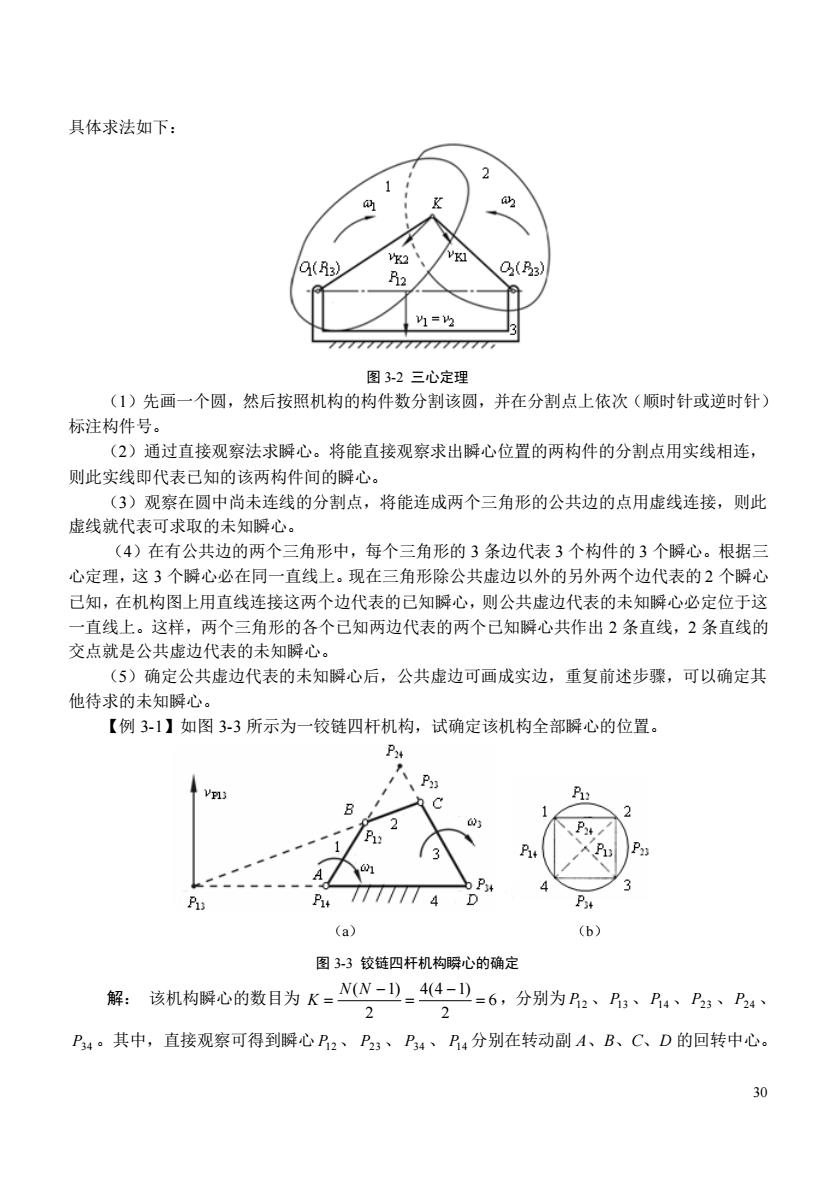
30 具体求法如下: 图 3-2 三心定理 (1)先画一个圆,然后按照机构的构件数分割该圆,并在分割点上依次(顺时针或逆时针) 标注构件号。 (2)通过直接观察法求瞬心。将能直接观察求出瞬心位置的两构件的分割点用实线相连, 则此实线即代表已知的该两构件间的瞬心。 (3)观察在圆中尚未连线的分割点,将能连成两个三角形的公共边的点用虚线连接,则此 虚线就代表可求取的未知瞬心。 (4)在有公共边的两个三角形中,每个三角形的 3 条边代表 3 个构件的 3 个瞬心。根据三 心定理,这 3 个瞬心必在同一直线上。现在三角形除公共虚边以外的另外两个边代表的 2 个瞬心 已知,在机构图上用直线连接这两个边代表的已知瞬心,则公共虚边代表的未知瞬心必定位于这 一直线上。这样,两个三角形的各个已知两边代表的两个已知瞬心共作出 2 条直线,2 条直线的 交点就是公共虚边代表的未知瞬心。 (5)确定公共虚边代表的未知瞬心后,公共虚边可画成实边,重复前述步骤,可以确定其 他待求的未知瞬心。 【例 3-1】如图 3-3 所示为一铰链四杆机构,试确定该机构全部瞬心的位置。 (a) (b) 图 3-3 铰链四杆机构瞬心的确定 解: 该机构瞬心的数目为 6 2 4(4 1) 2 ( 1) = − = − = N N K ,分别为 P12 、P13 、P14 、P23 、P24 、 P34 。其中,直接观察可得到瞬心 P12 、 P23 、 P34 、 P14 分别在转动副 A、B、C、D 的回转中心

P,和P,则需借助于三心定理确定,由于构件1、2、3的三个瞬心P2、P,、乃,应位于同一条 直线上,构件1、4、3三个瞬心乃4、P4、P3也应位于同一条直线上,因此两直线的交点即瞬 心P:同理,直线B2B,和P乃4的交点即瞬心P4 活动构件1、2、3与机架4之间的瞬心P4、P24、P4为绝对瞬心,而活动构件之间的瞬心 2、P23、乃3则为相对瞬心 利用三心定理求瞬心时,为了迅速准确地找到其位置,有两种方法: 其一是“下标同号消去法”,如图33所示,P:一定在P2、P:的连接线上,也一定在P4~ P:的连接线上,两线的交点即B:。一条直线上的三个瞬心,其中一个的下标一定是另外两个 清去相同下标后的组合。 其二是“解心多边形法”,如图33左上角所示,以构件编号表示多边形的顶点,任意两顶 点的连线表示相应两构件的解心。首先把直接成副的两构件解心P2、P:丶P4、R4,在瞬心 多边形中连成实线,把待求的不直接成刚的两构件瞬心P,、P4连成虚线。根据三心定理,在 瞬心多边形中,任意三角形的三条边所代表的三个瞬心均共线。因此,求未知瞬心时,可在瞬心 多边形中找到以代表该瞬心的虚线为公共边的两个三角形,在机构图中作出相应的两条直线,其 交点即为所求。例如,代表未知瞬心P1:的虚线是△123和△143的公共边,所以它既与B2、P3 共线又与P4、P4共线,连接P2、P:和P4、P4,其交点为P:。 利用瞬心多边形,特别有助于确定构件数目较多的机构的瞬心。 3.3.3瞬心在机构速度分析中的应用 下面举例说明利用速度瞬心对机构进行速度分析的方法。 1.求线速度 【例3-2】如图34所示的凸轮机构,已知各构件的尺寸和凸轮转速,求推杆2的速度2。 解:首先通过直接观察求得瞬心P:和P3,然后根据三心定律和公法线n求得瞬心P2的 位置。由此求得瞬心P2的速度 y2=P2=4(R3P2)m RP2长度直接从图上量取, 乃3→ 图34图解法求凸轮机构的线速度
31 P13 和 P24 则需借助于三心定理确定,由于构件 1、2、3 的三个瞬心 P12 、 P23 、P13 应位于同一条 直线上,构件 1、4、3 三个瞬心 P14 、P34、P13 也应位于同一条直线上,因此两直线的交点即瞬 心 P13 ;同理,直线 P12P14 和 P23P34 的交点即瞬心 P24 。 活动构件 1、2、3 与机架 4 之间的瞬心 P14 、 P24 、P34 为绝对瞬心,而活动构件之间的瞬心 P12、 P23 、 P13 则为相对瞬心。 利用三心定理求瞬心时,为了迅速准确地找到其位置,有两种方法: 其一是“下标同号消去法”,如图 3-3 所示, P13 一定在 P12 、P23 的连接线上,也一定在 P14 、 P34 的连接线上,两线的交点即 P13 。一条直线上的三个瞬心,其中一个的下标一定是另外两个 消去相同下标后的组合。 其二是“瞬心多边形法”,如图 3-3 左上角所示,以构件编号表示多边形的顶点,任意两顶 点的连线表示相应两构件的瞬心。首先把直接成副的两构件瞬心 P12 、 P23 、 P34 、 P14 ,在瞬心 多边形中连成实线,把待求的不直接成副的两构件瞬心 P13 、 P24 连成虚线。根据三心定理,在 瞬心多边形中,任意三角形的三条边所代表的三个瞬心均共线。因此,求未知瞬心时,可在瞬心 多边形中找到以代表该瞬心的虚线为公共边的两个三角形,在机构图中作出相应的两条直线,其 交点即为所求。例如,代表未知瞬心 P13 的虚线是 123 和 143 的公共边,所以它既与 P12 、 P23 共线又与 P14 、 P34 共线,连接 P12 、 P23 和 P14 、 P34 ,其交点为 P13 。 利用瞬心多边形,特别有助于确定构件数目较多的机构的瞬心。 3.3.3 瞬心在机构速度分析中的应用 下面举例说明利用速度瞬心对机构进行速度分析的方法。 1.求线速度 【例 3-2】如图 3-4 所示的凸轮机构,已知各构件的尺寸和凸轮转速 1 ,求推杆 2 的速度 2 v 。 解: 首先通过直接观察求得瞬心 P13 和 P23 ,然后根据三心定律和公法线 n-n 求得瞬心 P12 的 位置。由此求得瞬心 P12 的速度 2 P12 1 13 12 1 v = v = (P P ) P13P12 长度直接从图上量取。 图 3-4 图解法求凸轮机构的线速度

2.求角速度 1)铰链机构 【例33】如图3-3所示的铰链四杆机构,已知各构件的尺寸和原动件1的角速度,试求 构件3的角速度0,和角速比a,1o,。 解:将乃,视为构件1上的点,则有 YPB =0lP4P13 将P,视为构件3上的点,则有 VPB =@3P34P13 由瞬心的定义可得 0lp14n3=03lp34P13 转换后得 -p34pB-4 3lp14p3P43 上式表明,两构件之间的角速比©,/,(即传动比)与该两构件的绝对瞬心P4、P4至相 对瞬心乃,的距离成反比。 此关系可以推广到平面机构中任意两构件1与j之间(设构件4为机架),即 4-乃E (3-2) @j PiP 若相对瞬心P在绝对瞬心P4、P4之间,则构件1与j的转向相反:否则,转向相同。 【例34】如图3-5所示为按长度比例尺4,画出的平锻机工件夹紧机构运动简图,该机构是 一个复杂的平面Ⅲ级机构。已知原动件AB的角速度@,的大小和方向(如图所示),求02、, 04、的大小及方向。 解:由于构件2上点B的速度方向及大小已知(=,AB4),如果能求出其绝对瞬心P6, 则o,和vc可以求出。如果再能求出P6,则根据vc可以求出o,、'。和vE,于是可以解出o,和 @。所以解题的关键在于求出绝对瞬心P6与P6的位置。P6和P6的位置可按以下方法求出。 标出图中各铰链所示的瞬心B6、2、P3、P4、5、P6和P6。根据三心定理及已知的 瞬心,P6应位于直线P5P6与直线P4P6的交点上,在图上首先作出P6,从而可作出两条直 线R6B与P6B,在图上作出其交点即求得P6。按前面的分析得
32 2.求角速度 1)铰链机构 【例 3-3】如图 3-3 所示的铰链四杆机构,已知各构件的尺寸和原动件 1 的角速度 1,试求 构件 3 的角速度 3 和角速比 1 3 / 。 解:将 P13 视为构件 1 上的点,则有 P13 1 P14P13 v = l 将 P13 视为构件 3 上的点,则有 P13 3 P34P13 v = l 由瞬心的定义可得 1 P14P13 3 P34P13 l = l 转换后得 P34P13 P14P13 3 1 l l = 或 14 13 34 13 P14P13 P34P13 3 1 P P P P l l = = 上式表明,两构件之间的角速比 1 3 / (即传动比)与该两构件的绝对瞬心 P14 、 P34 至相 对瞬心 P13 的距离成反比。 此关系可以推广到平面机构中任意两构件 i 与 j 之间(设构件 4 为机架),即 i4 ij j4 j j i P P P Pi = (3-2) 若相对瞬心 Pij 在绝对瞬心 Pi4 、 Pj4 之间,则构件 i 与 j 的转向相反;否则,转向相同。 【例 3-4】如图 3-5 所示为按长度比例尺 1 画出的平锻机工件夹紧机构运动简图,该机构是 一个复杂的平面Ⅲ级机构。已知原动件 AB 的角速度 1 的大小和方向(如图所示),求 2 、 3 、 4 、5 的大小及方向。 解:由于构件 2 上点 B 的速度方向及大小已知( B 1 AB l v = ),如果能求出其绝对瞬心 P26 , 则 2 和 C v 可以求出。如果再能求出 P36,则根据 C v 可以求出 3、 D v 和 E v ,于是可以解出 4 和 5 。所以解题的关键在于求出绝对瞬心 P26 与 P36 的位置。 P36 和 P26 的位置可按以下方法求出。 标出图中各铰链所示的瞬心 P16 、P12 、P23 、P34 、P35、P46 和 P56 。根据三心定理及已知的 瞬心, P36 应位于直线 P35P56 与直线 P34P46 的交点上,在图上首先作出 P36 ,从而可作出两条直 线 P16P12 与 P36P23 ,在图上作出其交点即求得 P26 。按前面的分析得