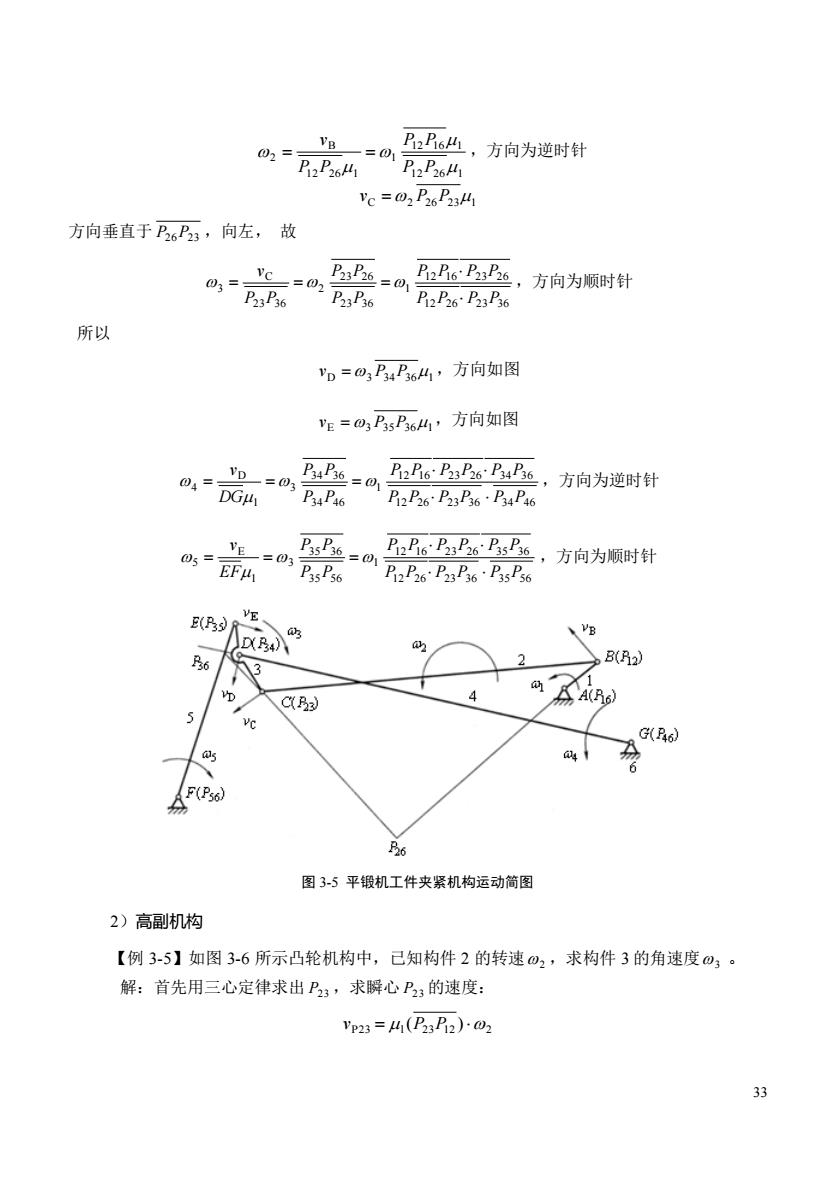
P丛,方向为逆时针 Ra乃4片 Vc=02P26P2s41 方向垂直于P6P,向左,故 P凸6乃上,方向为顺时针 PaPas PaPe PPi 所以 "p=034P64,方向如图 E=0P5P64,方向如图 PB6乃s乃B6,方向为逆时针 pPaP PaPe PaPa VE =03 P26326s6 ,方向为顺时针 P2P26P3P6·PsP6 g 2 B(R2) C A(R6) 5 (P56) 6 图3-5平锻机工件夹紧机构运动简图 2)高副机构 【例3-5】如图3-6所示凸轮机构中,已知构件2的转速2,求构件3的角速度o;。 解:首先用三心定律求出P23,求瞬心P2:的速度: Yp23=4(P2)2
33 12 26 1 12 16 1 1 12 26 1 B 2 P P P P P P v = = ,方向为逆时针 C 2 P26P231 v = 方向垂直于 P26P23 ,向左, 故 12 26 23 36 12 16 23 26 1 23 36 23 26 2 23 36 C 3 P P P P P P P P P P P P P P v = = = ,方向为顺时针 所以 D 3 P34P361 v = ,方向如图 E 3 P35P361 v = ,方向如图 12 26 23 36 34 46 12 16 23 26 34 36 1 34 46 34 36 3 1 D 4 P P P P P P P P P P P P P P P P DG v = = = ,方向为逆时针 12 26 23 36 35 56 12 16 23 26 35 36 1 35 56 35 36 3 1 E 5 P P P P P P P P P P P P P P P P EF v = = = ,方向为顺时针 图 3-5 平锻机工件夹紧机构运动简图 2)高副机构 【例 3-5】如图 3-6 所示凸轮机构中,已知构件 2 的转速 2 ,求构件 3 的角速度 3 。 解:首先用三心定律求出 P23 ,求瞬心 P23 的速度: P23 l 23 12 2 v = (P P )

Vp23=41(P233)03 所以 03=2(P/PP3).方向与02相反。 【例3-6】如图37所示为一直动从动件凸轮机构。设己知各构件的尺寸和原动件1的角速 度0,求从动件2的速度y2。 解:因为构件2作平动,所以利用瞬心P2是构件1和2的等速重合点,即可求得2。 由于构件1、2组成高副,所以瞬心乃2在过接触点K处的公法线-上:又由三心定理知, 瞬心P2与P,、P,共线。因此过R,作P,的方向线与m-n线的交点即为瞬心P2。 2=yp2=1R2R341 y2方向向上,如图37所示。 B3→ 、刀 53 ⊙13 1 图36图解法求高副机构的角速度 图37直动从动件凸轮机构 利用速度瞬心法对简单机构的速度分析非常简便。但对于包含构件数目较多的机构,由于瞬 心数目较多,使得求解困难。需要特别说明的是,速度瞬心法仅限于对机构的速度分析,不便用 于加速度分析。 3.3用相对运动图解法对机构进行运动分析 相对运动图解法(relative kinematic graphic method)也称为矢量方程图解法(vector graphic method),所依据的是理论力学中的运动合成原理。在对机构进行速度、加速度分析时,根据运 动合成原理列出速度、加速度运动矢量方程,按矢量运算作图求解。下面就在机构运动分析中所 遇到的两种不同情况对其基本原理和方法加以说明。 3.3.1作平面运动的同一构件上两点间的运动分析 如图3-8a所示为铰链四杆机构运动简图。已知各构件的尺寸及原动件1以等角速度0,逆时 针方向转动,求机构在图示位置时构件2、3的角速度o2、o,和角加速度a2、α,以及构件2
34 P23 l 23 13 3 v = (P P ) 所以 ( / ) 3 2 P23P13 P23P13 = ,方向与 2 相反。 【例 3-6】如图 3-7 所示为一直动从动件凸轮机构。设已知各构件的尺寸和原动件 1 的角速 度 1 ,求从动件 2 的速度 2 v 。 解:因为构件 2 作平动,所以利用瞬心 P12 是构件 1 和 2 的等速重合点,即可求得 2 v 。 由于构件 1、2 组成高副,所以瞬心 P12 在过接触点 K 处的公法线 n-n 上;又由三心定理知, 瞬心 P12 与 P13 、 P23 共线。因此过 P13 作 P23 的方向线与 n-n 线的交点即为瞬心 P12 。 2 Pl2 1P12P13l v = v = 2 v 方向向上,如图 3-7 所示。 图 3-6 图解法求高副机构的角速度 图 3-7 直动从动件凸轮机构 利用速度瞬心法对简单机构的速度分析非常简便。但对于包含构件数目较多的机构,由于瞬 心数目较多,使得求解困难。需要特别说明的是,速度瞬心法仅限于对机构的速度分析,不便用 于加速度分析。 3.3 用相对运动图解法对机构进行运动分析 相对运动图解法(relative kinematic graphic method)也称为矢量方程图解法(vector graphic method),所依据的是理论力学中的运动合成原理。在对机构进行速度、加速度分析时,根据运 动合成原理列出速度、加速度运动矢量方程,按矢量运算作图求解。下面就在机构运动分析中所 遇到的两种不同情况对其基本原理和方法加以说明。 3.3.1 作平面运动的同一构件上两点间的运动分析 如图 3-8a 所示为铰链四杆机构运动简图。已知各构件的尺寸及原动件 1 以等角速度 1 逆时 针方向转动,求机构在图示位置时构件 2、3 的角速度 2 、3 和角加速度 2 、 3 ,以及构件 2

上点E的速度ve和加速度ae。 用相对运动图解法进行运动分析时,应沿着机构的运动传递顺序,从与运动已知的原动件相 连的杆组开始,以杆组为单位依次进行。首先确定杆组中外接副的运动(往往是已知的),其次 确定杆组内接副的运动,然后再确定构件上一般点的运动。 4 (a)铰链四杆机构运动简图 (b)速度多边形 (c)加速度多边形 图38同一构件上两点之间的运动图解分析 1.列出运动矢量方程式 较链四杆机构仅含有一个Ⅱ级杆组BCD,且外接副点B、D的运动已知,所以先求内接副 点C的运动。而点C和B同在连杆2上,选运动己知的点B为基点,由运动合成原理,点C的 运动可视为随着基点B作平动与绕着基点B作相对转动的合成。所以点C的速度和加速度ac 的矢量方程分别表示为 6=g+v (3-2) 方向:⊥CD⊥AB⊥BC 大小:?OlAg? ac=a吧+a=ag+a+ad (3-3)》 方向: C→D⊥CDB→AC→B⊥BC 大小: olcD?o2 IAB lBc? 式中,y、a、a为点C相对于点B的相对速度、相对法向加速度和相对切向加速度: a、a心分别为点C的绝对法向加速度和切向加速度。 为了减少方程中未知量的数目,将转动加速度分解为法向和切向两个分量,每一项的大小 和方向均示于式中。在式(32)中,仅、的大小未知,而在式(3-3)中,经过速度分析 之后a品也为已知,仅有心、a心的大小未知,故每个方程组仅包含两个未知量,可以用作图 法求解
35 上点 E 的速度 E v 和加速度 E 。 用相对运动图解法进行运动分析时,应沿着机构的运动传递顺序,从与运动已知的原动件相 连的杆组开始,以杆组为单位依次进行。首先确定杆组中外接副的运动(往往是已知的),其次 确定杆组内接副的运动,然后再确定构件上一般点的运动。 (a) 铰链四杆机构运动简图 (b) 速度多边形 (c) 加速度多边形 图 3-8 同一构件上两点之间的运动图解分析 1.列出运动矢量方程式 铰链四杆机构仅含有一个Ⅱ级杆组 BCD,且外接副点 B、D 的运动已知,所以先求内接副 点 C 的运动。而点 C 和 B 同在连杆 2 上,选运动已知的点 B 为基点,由运动合成原理,点 C 的 运动可视为随着基点 B 作平动与绕着基点 B 作相对转动的合成。所以点 C 的速度 C v 和加速度 Ca 的矢量方程分别表示为 C B CB v = v + v (3-2) 方向: ⊥ CD ⊥ AB ⊥ BC 大小: ? 1 AB l ? t CB n B CB t C n C C a = a + a = a + a + a (3-3) 方向: C → D ⊥ CD B → A C → B ⊥ BC 大小: CD 2 3 l ? AB 2 1 l BC 2 2 l ? 式中, CB v 、 n CB a 、 t CB a 为点 C 相对于点 B 的相对速度、相对法向加速度和相对切向加速度; n Ca 、 t Ca 分别为点 C 的绝对法向加速度和切向加速度。 为了减少方程中未知量的数目,将转动加速度分解为法向和切向两个分量,每一项的大小 和方向均示于式中。在式(3-2)中,仅 C v 、 CB v 的大小未知,而在式(3-3)中,经过速度分析 之后 n CB a 也为已知,仅有 t Ca 、 t CB a 的大小未知,故每个方程组仅包含两个未知量,可以用作图 法求解

2.按矢量方程式作图求解 实际速度(m/s) 速度比例尺山,“表示该实际速度的图示长度(mm,即图中每1mm所代表的速度大小。 实际加速度(m/s2) 加速度比例4,一表示该实等速度的图示长度(,即图中每mm所代表的加速度 大小 1)按速度矢量方程作矢量运算图解 如图3-8b所示,任取一点p作为速度极点。从点p出发作代表v。的矢量pb(⊥AB,且 pb=B14v),再分别过点b和p作代表c的方向线bc(⊥BC),代表的方向线pc(⊥CD), 两者相交于点c,则 构件2的角速度则为 是瓷 可将©平移至机构图上的点C,绕点B的转向即为o,的方向(顺时针方向)。 构件3的角速度为 宏篇 将C平移至机构图上的点C,绕点D的转向即为@,的方向(逆时针方向)。 2)按加速度矢量方程作矢量运算图解 如图3-8c所示,任取一点p作为加速度极点。从点p出发作代表ae的矢量pb(∥AB, 由机构图上的点B指向点A,且p方=a14,):再分别过点b和p,作代表品的矢量B。(∥ BC,由点C指向点B)和代表a是的矢量pc(ICD,由点C指向点D片然后再分别过点c和 c"作代表am的方向线c(⊥BC)和代表a6的方向线c"c(⊥CD),两者相交于点c, a=4c"c,a=4c”c 则构件2的角加速度为 acB tac"c a2=Inc M BC 可将a平移至机构图上的点C,绕点B的转向即为a2的方向(逆时针方向)
36 2.按矢量方程式作图求解 表示该实际速度的图示长度( ) 实际速度( ) 速度比例尺 mm m /s V = ,即图中每 1mm 所代表的速度大小。 表示该实际加速度的图示长度( ) 实际加速度( ) 加速度比例尺 mm m /s 2 a = ,即图中每 1mm 所代表的加速度 大小。 1)按速度矢量方程作矢量运算图解 如图 3-8b 所示,任取一点 p 作为速度极点。从点 p 出发作代表 B v 的矢量 pb ( ⊥ AB ,且 B V pb = v / ),再分别过点 b 和 p 作代表 CB v 的方向线 bc ( ⊥ BC ),代表 C v 的方向线 pc ( ⊥ CD ), 两者相交于点 c,则 v pc C = V , v bc CB = V 构件 2 的角速度则为 BC bc l v 1 V BC CB 2 = = 可将 CB v 平移至机构图上的点 C,绕点 B 的转向即为 2 的方向(顺时针方向)。 构件 3 的角速度为 CD pc l v 1 V CD C 3 = = 将 C v 平移至机构图上的点 C,绕点 D 的转向即为 3 的方向(逆时针方向)。 2)按加速度矢量方程作矢量运算图解 如图 3-8c 所示,任取一点 p' 作为加速度极点。从点 p' 出发作代表 B a 的矢量 p'b' (∥AB, 由机构图上的点 B 指向点 A,且 B a p'b' = a / );再分别过点 b' 和 p' ,作代表 n CB a 的矢量 b'c" (∥ BC,由点 C 指向点 B)和代表 n Ca 的矢量 p' c' ' ' (//CD,由点 C 指向点 D);然后再分别过点 c" 和 c' ' ' 作代表 t CB a 的方向线 c"c' ( ⊥ BC)和代表 t Ca 的方向线 c' ' 'c' ( ⊥ CD), 两者相交于点 c' , 则 ' ' ' ' a t Ca = c c , " ' a t CB a = c c 则构件 2 的角加速度为 BC c c l a 1 a BC t CB 2 " ' = = 可将 t CB a 平移至机构图上的点 C,绕点 B 的转向即为 2 的方向(逆时针方向)