
第六章齿轮机构 内容提要 本章主要介绍齿轮机构的类型、特点及其应用:齿廓啮合的基本定律及渐开线齿廓的形成与 性质:渐开线标准直齿圆柱齿轮的基本参数与几何尺寸:渐开线齿廓的加工及变位齿轮与变位齿 轮传动:斜齿圆柱齿轮、圆锥齿轮与蜗杆传动机构,并简单介绍了其他类型的齿轮传动机构。重 点内容是齿轮的啮合原理与几何设计。 6.1概述 齿轮传动机构是机械传动中最主要、应用最为广泛的一种传动机构,可用来传递任意两轴之 间的运动和动力。 6.1.1齿轮传动的应用和特点 齿轮传动广泛地应用在工程机械、矿山机械、治金机械、各种机床及仪器、仪表工业等行业, 齿轮传动可用来传递回转运动,同时还可以用来转换直线与回转运动。与带传动、链传动等比较, 齿轮传动具有如下主要优点: (1)齿轮传动能保证瞬时传动比的恒定,传动平稳,传动比准确。 (2)结构紧凑、工作可靠、效率高、寿命长。 (3)传动的功率、速度和尺寸范围大。传递功率可以从不足一瓦至几十万千瓦:线速度可 达300ms:齿轮直径可以从几毫米至几十米。 齿轮传动也存在一些缺点,主要有:齿轮的齿数为整数,不能实现无级变速:啮合传动有一 定的噪声:需要有专门制造齿轮的设备,要求较高的制造和安装精度,加工成本高:中心距过大 时齿轮传动机构结构庞大、笨重,不适宜远距离传动。 6.1.2齿轮传动机构的类型 齿轮传动机构的类型很多,按照齿廓曲线的种类可分为:渐开线齿轮传动机构、摆线齿轮传 动机构和圆弧齿轮传动机构等。按照齿轮的形状,可分为:圆形齿轮传动机构和非圆形齿轮传动 机构。本章将讨论渐开线圆形齿轮传动机构。 在圆形齿轮机构中,根据两个传动轴线的相对位置可分为:平行轴齿轮传动机构、相交轴齿 106
106 第六章 齿轮机构 内容提要 本章主要介绍齿轮机构的类型、特点及其应用;齿廓啮合的基本定律及渐开线齿廓的形成与 性质;渐开线标准直齿圆柱齿轮的基本参数与几何尺寸;渐开线齿廓的加工及变位齿轮与变位齿 轮传动;斜齿圆柱齿轮、圆锥齿轮与蜗杆传动机构,并简单介绍了其他类型的齿轮传动机构。重 点内容是齿轮的啮合原理与几何设计。 6.1 概述 齿轮传动机构是机械传动中最主要、应用最为广泛的一种传动机构,可用来传递任意两轴之 间的运动和动力。 6.1.1 齿轮传动的应用和特点 齿轮传动广泛地应用在工程机械、矿山机械、冶金机械、各种机床及仪器、仪表工业等行业, 齿轮传动可用来传递回转运动,同时还可以用来转换直线与回转运动。与带传动、链传动等比较, 齿轮传动具有如下主要优点: (1)齿轮传动能保证瞬时传动比的恒定,传动平稳,传动比准确。 (2)结构紧凑、工作可靠、效率高、寿命长。 (3)传动的功率、速度和尺寸范围大。传递功率可以从不足一瓦至几十万千瓦;线速度可 达 300m/s;齿轮直径可以从几毫米至几十米。 齿轮传动也存在一些缺点,主要有:齿轮的齿数为整数,不能实现无级变速;啮合传动有一 定的噪声;需要有专门制造齿轮的设备,要求较高的制造和安装精度,加工成本高;中心距过大 时齿轮传动机构结构庞大、笨重,不适宜远距离传动。 6.1.2 齿轮传动机构的类型 齿轮传动机构的类型很多,按照齿廓曲线的种类可分为:渐开线齿轮传动机构、摆线齿轮传 动机构和圆弧齿轮传动机构等。按照齿轮的形状,可分为:圆形齿轮传动机构和非圆形齿轮传动 机构。本章将讨论渐开线圆形齿轮传动机构。 在圆形齿轮机构中,根据两个传动轴线的相对位置可分为:平行轴齿轮传动机构、相交轴齿

轮传动机构和交错轴齿轮传动机构 1,平行轴齿轮机构 两齿轮轴线相互平行的齿轮传动机构属于平面齿轮传动机构。常见的类型有直齿圆柱齿轮、 斜齿圆柱齿轮、人字齿轮传动和齿轮齿条传动。 1)直齿圆柱齿轮传动(spur gears) 直齿圆柱齿轮(spur gear)轮齿的方向与齿轮的轴线方向一致。当齿轮的轮齿在圆柱的外表 面上时称为外齿轮,如图6-1a中的两个齿轮和图6-b中的小齿轮:当轮齿在圆柱内表面上时称 为内齿轮,如图6-1b中的大齿轮。图6-1a所示的两个外齿轮啮合称为外啮合,外啮合传动时, 两齿轮转动方向相反:图61b所示的两一个内齿轮与一个外齿轮晒合时称为内啮合,内合传 动时,两齿轮的转动方向相同。直齿圆柱齿轮只能用于相互平行的两轴之间的传动。 2)斜齿圆柱齿轮传动(helical gears) 斜齿圆柱齿轮的轮齿方向与其轴线方向倾斜一个角度,这个角度称为螺旋角(helix angle)。 当两齿轮的螺旋角大小相同时,两齿轮轴线相互平行,称这种传动形式为斜齿轮传动。如图6-2 所示为外啮合斜齿圆柱齿轮传动(两齿轮螺旋角大小相同、方向相反);如图6-2b所示为内啮 合斜齿轮传动(两齿轮螺旋角大小与方向均相同)。 (a)外啮合 (b)内啮合 (a)外呐合 (b)内啮合 图61直齿圆柱齿轮传动 图6-2斜齿圆柱齿轮传动 3)人字齿轮传动(herringbone gears) 如图63错误:未找到引用源。所示的这种齿轮轮齿的方向呈人字形,可以看成是由两个螺 旋角大小相等、旋向相反的斜齿轮对称组合而成,故称为人字齿轮传动。 4)齿轮齿条传动(pinion and rack drive) 当齿轮的齿数趋于无穷多时,外齿轮就演变成齿条(ck),如图64所示。啮合时,齿轮转 动,齿条直线移动。 图6-3人字齿轮传动 图64齿轮齿条传动 2.相交轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线相交于一点,轴线交角通常为90°,如图65所示的圆锥齿 107
107 轮传动机构和交错轴齿轮传动机构。 1.平行轴齿轮机构 两齿轮轴线相互平行的齿轮传动机构属于平面齿轮传动机构。常见的类型有直齿圆柱齿轮、 斜齿圆柱齿轮、人字齿轮传动和齿轮齿条传动。 1)直齿圆柱齿轮传动(spur gears) 直齿圆柱齿轮(spur gear)轮齿的方向与齿轮的轴线方向一致。当齿轮的轮齿在圆柱的外表 面上时称为外齿轮,如图 6-1a 中的两个齿轮和图 6-1b 中的小齿轮;当轮齿在圆柱内表面上时称 为内齿轮,如图 6-1b 中的大齿轮。图 6-1a 所示的两个外齿轮啮合称为外啮合,外啮合传动时, 两齿轮转动方向相反;图 6-1b 所示的两一个内齿轮与一个外齿轮啮合时称为内啮合,内啮合传 动时,两齿轮的转动方向相同。直齿圆柱齿轮只能用于相互平行的两轴之间的传动。 2)斜齿圆柱齿轮传动(helical gears) 斜齿圆柱齿轮的轮齿方向与其轴线方向倾斜一个角度,这个角度称为螺旋角(helix angle)。 当两齿轮的螺旋角大小相同时,两齿轮轴线相互平行,称这种传动形式为斜齿轮传动。如图 6-2a 所示为外啮合斜齿圆柱齿轮传动(两齿轮螺旋角大小相同、方向相反);如图 6-2b 所示为内啮 合斜齿轮传动(两齿轮螺旋角大小与方向均相同)。 (a)外啮合 (b)内啮合 (a)外啮合 (b)内啮合 图 6-1 直齿圆柱齿轮传动 图 6-2 斜齿圆柱齿轮传动 3)人字齿轮传动(herringbone gears) 如图 6-3 错误!未找到引用源。所示的这种齿轮轮齿的方向呈人字形,可以看成是由两个螺 旋角大小相等、旋向相反的斜齿轮对称组合而成,故称为人字齿轮传动。 4)齿轮齿条传动(pinion and rack drive) 当齿轮的齿数趋于无穷多时,外齿轮就演变成齿条(rack),如图 6-4 所示。啮合时,齿轮转 动,齿条直线移动。 图 6-3 人字齿轮传动 图 6-4 齿轮齿条传动 2.相交轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线相交于一点,轴线交角通常为 90°,如图 6-5 所示的圆锥齿
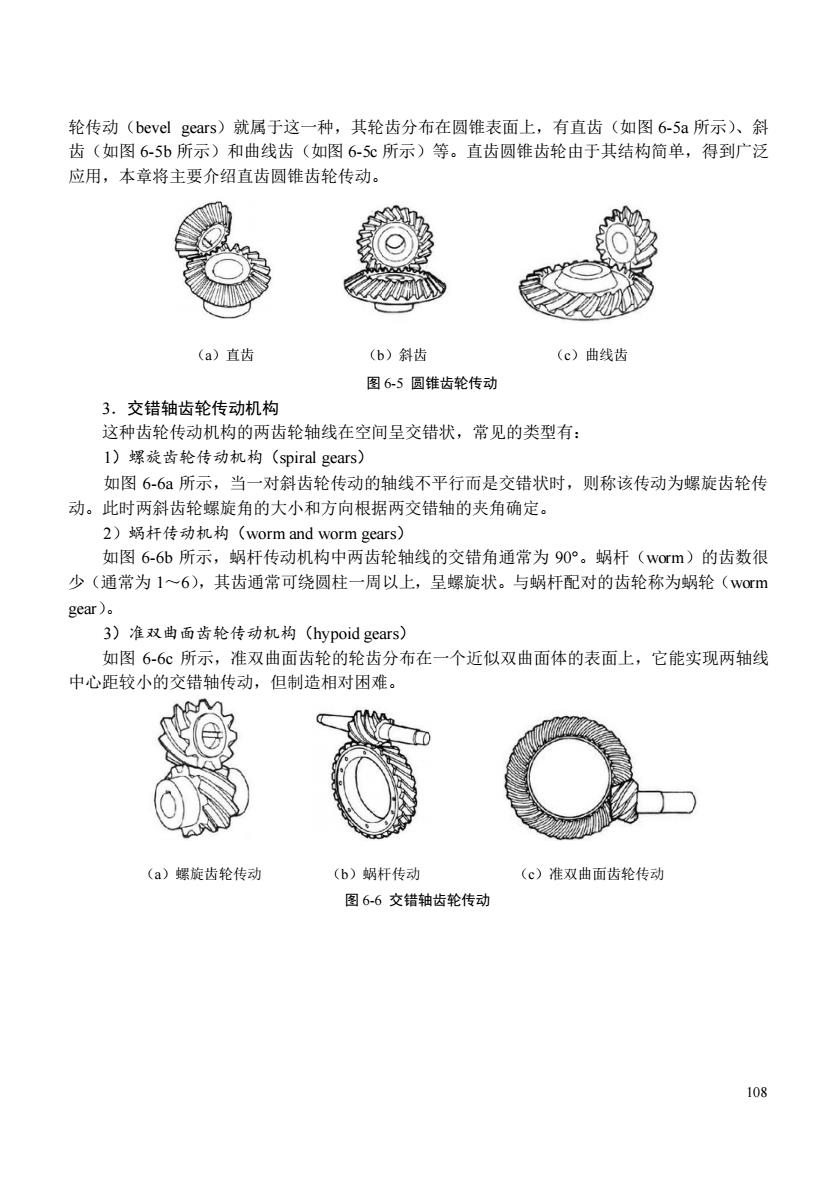
轮传动(bevel gears)就属于这一种,其轮齿分布在圆锥表面上,有直齿(如图6-5a所示)、斜 齿(如图6-5b所示)和曲线齿(如图65心所示)等。直齿圆锥齿轮由于其结构简单,得到广泛 应用,本章将主要介绍直齿圆锥齿轮传动。 (a)直齿 (b)斜齿 (c)曲线齿 图65圆锥齿轮传动 3.交错轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线在空间呈交错状,常见的类型有: 1)螺旋齿轮传动机构(spiral gears) 如图6-6a所示,当一对斜齿轮传动的轴线不平行而是交错状时,则称该传动为螺旋齿轮传 动。此时两斜齿轮螺旋角的大小和方向根据两交错轴的夹角确定。 2)蜗杆传动机构(worm and worm gears) 如图6-6b所示,蜗杆传动机构中两齿轮轴线的交错角通常为90°。蜗杆(wom)的齿数很 少(通常为1~6),其齿通常可绕圆柱一周以上,呈螺旋状。与蜗杆配对的齿轮称为蜗轮(w0m gea). 3)准双曲面齿轮传动机构(hypoid gears) 如图6-6c所示,准双曲面齿轮的轮齿分布在一个近似双曲面体的表面上,它能实现两轴线 中心距较小的交错轴传动,但制造相对困难。 (a)螺旋齿轮传动 (b)蜗杆传动 (c)准双曲面齿轮传动 图6-6交错轴齿轮传动 108
108 轮传动(bevel gears)就属于这一种,其轮齿分布在圆锥表面上,有直齿(如图 6-5a 所示)、斜 齿(如图 6-5b 所示)和曲线齿(如图 6-5c 所示)等。直齿圆锥齿轮由于其结构简单,得到广泛 应用,本章将主要介绍直齿圆锥齿轮传动。 (a)直齿 (b)斜齿 (c)曲线齿 图 6-5 圆锥齿轮传动 3.交错轴齿轮传动机构 这种齿轮传动机构的两齿轮轴线在空间呈交错状,常见的类型有: 1)螺旋齿轮传动机构(spiral gears) 如图 6-6a 所示,当一对斜齿轮传动的轴线不平行而是交错状时,则称该传动为螺旋齿轮传 动。此时两斜齿轮螺旋角的大小和方向根据两交错轴的夹角确定。 2)蜗杆传动机构(worm and worm gears) 如图 6-6b 所示,蜗杆传动机构中两齿轮轴线的交错角通常为 90°。蜗杆(worm)的齿数很 少(通常为 1~6),其齿通常可绕圆柱一周以上,呈螺旋状。与蜗杆配对的齿轮称为蜗轮(worm gear)。 3)准双曲面齿轮传动机构(hypoid gears) 如图 6-6c 所示,准双曲面齿轮的轮齿分布在一个近似双曲面体的表面上,它能实现两轴线 中心距较小的交错轴传动,但制造相对困难。 (a)螺旋齿轮传动 (b)蜗杆传动 (c)准双曲面齿轮传动 图 6-6 交错轴齿轮传动

6.2齿廓啮合基本定律 齿轮传动是靠主动轮的齿廓依次推动从动轮的齿廓来实现的,齿廓曲线形状直接影响两齿轮 的瞬时传动比及轮齿的抗破坏能力,因此需要研究齿廊形状与齿轮机构传动之间的关系,即齿廓 啮合基本定律。 0所示为两齿廓啮合的情况,两齿廓在K点相切。过K点作两齿廓的公法线与两齿轮中 心连线O,O2相交于P点。由瞬心的概念可知,P点为两齿轮的瞬心,即 p1=p2=0O,P=0,O,P 若将一对相互啮合齿轮的转速(或角速度)之比称为传动比,则齿轮1与齿轮2的传动比 6÷兴器 (0-1) 图6-7中的P点称为两齿轮的啮合节点,简称节点(pitch point)。上式表明,一对齿轮在任 意位置啮合时的传动比,都与中心连线O,O,被节点P分成的两段长度成反比。这一规律称为齿 廓啮合的基本定律。 10 月=2 图6-7齿廓咕合基本定律 如果一对相互啮合齿轮的齿廓在不同的位置上啮合时,其节点P的位置是变化的,则两齿 轮的传动比就是变化的:若节点P的位置是固定的,则两个齿轮的传动比就是恒定的。齿轮传 动的最基本的要求是在啮合的过程中传动比保持恒定,满足这一要求的一对齿廓称为共轭齿廓。 理论上,只要给出两个齿轮的中心距、传动比和其中一个齿轮的齿廓曲线,就能求出组成一 对共轭齿廓的另一个齿轮的齿廓曲线。但考虑到设计、制造、安装和使用等因素,目前应用最多 的齿廓曲线是渐开线,其次是摆线,也有圆弧和抛物线等。 109
109 6.2 齿廓啮合基本定律 齿轮传动是靠主动轮的齿廓依次推动从动轮的齿廓来实现的,齿廓曲线形状直接影响两齿轮 的瞬时传动比及轮齿的抗破坏能力,因此需要研究齿廓形状与齿轮机构传动之间的关系,即齿廓 啮合基本定律。 0 所示为两齿廓啮合的情况,两齿廓在 K 点相切。过 K 点作两齿廓的公法线 n-n 与两齿轮中 心连线 O1O2 相交于 P 点。由瞬心的概念可知,P 点为两齿轮的瞬心,即 vP 1 = vP 2 =1O1P =2O2P 若将一对相互啮合齿轮的转速(或角速度)之比称为传动比,则齿轮 1 与齿轮 2 的传动比 O P O P n n i 1 2 2 1 2 1 12 = = = (0-1) 图 6-7 中的 P 点称为两齿轮的啮合节点,简称节点(pitch point)。上式表明,一对齿轮在任 意位置啮合时的传动比,都与中心连线 O1O2 被节点 P 分成的两段长度成反比。这一规律称为齿 廓啮合的基本定律。 图 6-7 齿廓啮合基本定律 如果一对相互啮合齿轮的齿廓在不同的位置上啮合时,其节点 P 的位置是变化的,则两齿 轮的传动比就是变化的;若节点 P 的位置是固定的,则两个齿轮的传动比就是恒定的。齿轮传 动的最基本的要求是在啮合的过程中传动比i保持恒定,满足这一要求的一对齿廓称为共轭齿廓。 理论上,只要给出两个齿轮的中心距、传动比和其中一个齿轮的齿廓曲线,就能求出组成一 对共轭齿廓的另一个齿轮的齿廓曲线。但考虑到设计、制造、安装和使用等因素,目前应用最多 的齿廓曲线是渐开线,其次是摆线,也有圆弧和抛物线等

6.3渐开线齿廓 6.3.1渐开线的形成与性质 如错误未找到引用源。所示,假想有一绳子缠绕在半径为,的圆周上,当从某一点A将绳 子拉离圆周表面时,其端点A的运动轨迹AK即称为该圆周的渐开线。该圆称为渐开线的基圆, 直线BK为渐开线的发生线,角日k称为AK段渐开线的展角 从渐开线的形成过程可知,渐开线具有以下性质: (I)发生线沿基圆滚过的长度BK等于基圆上被滚过的弧长AB,即BK=AB。 (2)渐开线上任意一点K的法线BK一定与其基圆相切。也就是说,切于基圆的直线必为 渐开线上某点的法线。 (3)发生线与基圆的切点B为渐开线在K点的曲率中心,而线段BK是渐开线在点K处的 曲率半径。渐开线越接近于基圆的部分,其曲率半径越小、曲率越大。渐开线起点A处的曲率 半径为零。 (4)渐开线的形状取决于基圆的大小。如图69所示,基圆越大,渐开线越平直:当基圆 半径趋于无穷大时,渐开线将变成一条直线,直线齿廓(如齿条)是渐开线齿廓的一种特例。 图6-8浙开线形成与特点 图69基圆与渐开线形状的关系 (5)基圆内无渐开线。 (6)齿廓上不同位置上的压力角不同。如图6-8所示,若以点0为齿轮的转动中心,AK 为齿廓曲线,F为作用于K点的正压力,Vx为K点的速度。根据压力角的定义,F与YK所夹的 锐角aK称为渐开线上任一点K的压力角。由图可知∠BOK=aK,所以 a=∠BOK=acos月 (0-2) 上式表明渐开线齿廓上各点的压力角是不同的。基圆上的压力角(α)为零,越远离基圆压 力角越大。 110
110 6.3 渐开线齿廓 6.3.1 渐开线的形成与性质 如错误!未找到引用源。所示,假想有一绳子缠绕在半径为 b r 的圆周上,当从某一点 A 将绳 子拉离圆周表面时,其端点 A 的运动轨迹 AK 即称为该圆周的渐开线。该圆称为渐开线的基圆, 直线 BK 为渐开线的发生线,角 K 称为 AK 段渐开线的展角。 从渐开线的形成过程可知,渐开线具有以下性质: (1)发生线沿基圆滚过的长度 BK 等于基圆上被滚过的弧长 AB ,即 BK = AB 。 (2)渐开线上任意一点 K 的法线 BK 一定与其基圆相切。也就是说,切于基圆的直线必为 渐开线上某点的法线。 (3)发生线与基圆的切点 B 为渐开线在 K 点的曲率中心,而线段 BK 是渐开线在点 K 处的 曲率半径。渐开线越接近于基圆的部分,其曲率半径越小、曲率越大。渐开线起点 A 处的曲率 半径为零。 (4)渐开线的形状取决于基圆的大小。如图 6-9 所示,基圆越大,渐开线越平直;当基圆 半径趋于无穷大时,渐开线将变成一条直线,直线齿廓(如齿条)是渐开线齿廓的一种特例。 图 6-8 渐开线形成与特点 图 6-9 基圆与渐开线形状的关系 (5)基圆内无渐开线。 (6)齿廓上不同位置上的压力角不同。如图 6-8 所示,若以点 O 为齿轮的转动中心,AK 为齿廓曲线,F 为作用于 K 点的正压力, K v 为 K 点的速度。根据压力角的定义,F 与 K v 所夹的 锐角 K 称为渐开线上任一点 K 的压力角。由图可知 BOK = K ,所以 K b K arccos r r = BOK = (0-2) 上式表明渐开线齿廓上各点的压力角是不同的。基圆上的压力角( b )为零,越远离基圆压 力角越大。 ) )