
2.变速直线运动的路程 设某物体作直线运动,己知速度v=v(t)∈C[T,I2],且 v(t)≥0,求在运动时间内物体所经过的路程s 解决步骤: 1)大化小.在[☑,T2]中任意插入n-1个分点,将它分成 n个小段[t-1,t](i=1,2,n),在每个小段上物体经 过的路程为△s,(i=1,2,.,n) 2)常代变.任取5∈[1,],以(5)代替变速,得 △s,≈v(5i)A1(i=1,2,.,n) HIGH EDUCATION PRESS 返回 结束
2. 变速直线运动的路程 设某物体作直线运动, ( ) [ , ], C T1 T2 v v t 且 v(t) 0, 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 大化小. [ , ], i i 1 i t t 任取 将它分成 [ , ]( 1, 2, , ), 1 t t i n i i 在每个小段上物体经 2) 常代变. 以 ( )代替变速 , i v 得 i i i s v( )t [ , ] 1 , 在 T1 T2 中任意插入 n 个分点 s (i 1, 2, , n) i (i 1, 2,,n) 已知速度 机动 目录 上页 下页 返回 结束 n 个小段 过的路程为

3)近似和. n S≈ ∑(5)△ i=l 4)取极限. s lim ∑(5)△1 (= max△t,) 20 l<i<n 上述两个问题的共性 ·解决问题的方法步骤相同: “大化小,常代变,近似和,取极限” ·所求量极限结构式相同:特殊乘积和式的极限 HIGH EDUCATION PRESS
3) 近似和. i n i i s v t 1 ( ) 4) 取极限 . i n i i s v t 1 0 lim ( ) ( max ) 1 i i n t 上述两个问题的共性: • 解决问题的方法步骤相同 : “大化小 , 常代变 , 近似和 , 取极限 ” • 所求量极限结构式相同: 特殊乘积和式的极限 机动 目录 上页 下页 返回 结束

二、定积分定义(P225) 设函数f(x)定义在[a,b]上,若对[a,b]的任一种分法 a=X0<为<x2<<xn=b,令Ax,=x,-x,-1,任取 5,∈[x1,x-],只要元=max{△x,}→0时 ∑f(5)△x, l<i<n 1 总趋于确定的极限I,则称此极限I为函数f(x)在区间 [a,b]上的定积分,记作心f(x)dx 5 即 7wd-25a o ax xi-ix;bx 此时称f(x)在[a,b]上可积 HIGH EDUCATION PRESS 结球
o a b x 二、定积分定义 ( P225 ) 设函数 f (x)定义在[a,b]上, 若对[a, b]的任一种分法 , 0 1 2 a x x x x b n , i i i1 令 x x x 任取 [ , ] , i i i1 x x i 只要 max{ } 0时 1 i i n x i n i i f x 1 ( ) 总趋于确定的极限 I ,则称此极限 I 为函数 f (x) 在区间 [a, b]上的定积分, 1 x i x i1 x b a f (x)dx 即 b a f (x)dx i n i i f x 1 0 lim ( ) 此时称 f ( x ) 在 [ a , b ] 上可积 . 记作 机动 目录 上页 下页 返回 结束

积分上限 [a,b]称为积分区间 1f(x)dx lim∑f(5,)△x, i= 积分下限 被积函数 被积表达式 积分变量 积分和 定积分仅与被积函数及积分区间有关,而与积分 变量用什么字母表示无关,即 jf)dx=∫fo0d=∫fw)am HIGH EDUCATION PRESS
b a f (x)dx i n i i f x 1 0 lim ( ) 积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 积 分 和 [a, b] 称为积分区间 定积分仅与被积函数及积分区间有关 , 而与积分 变量用什么字母表示无关 , 即 b a f (x)dx b a f (t)d t b a f (u)d u 机动 目录 上页 下页 返回 结束
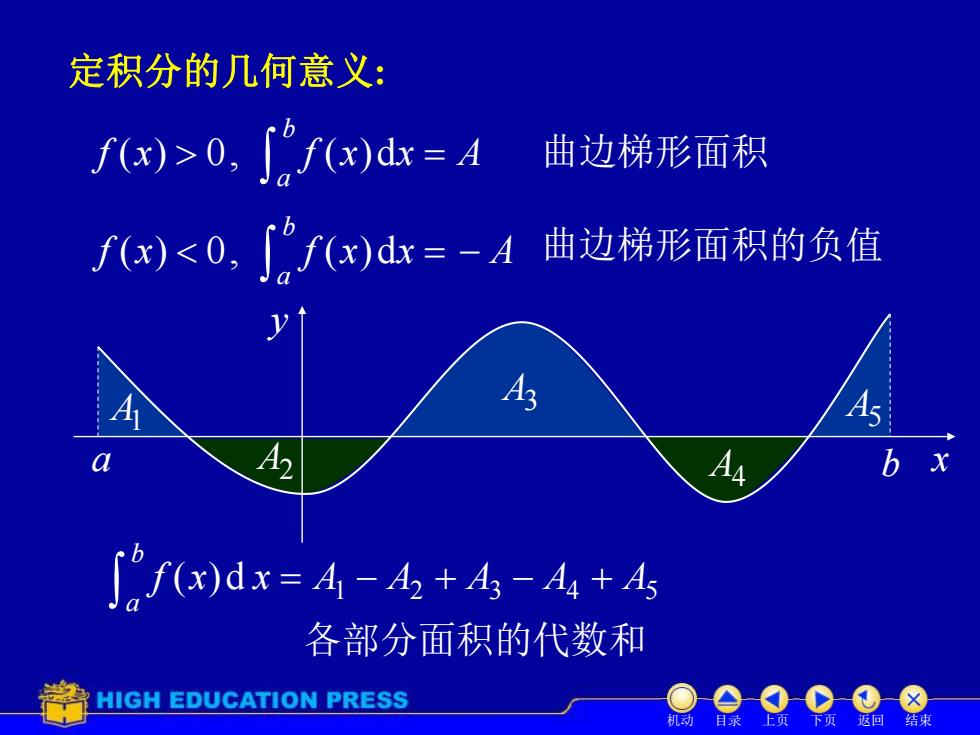
定积分的几何意义: f(x)>0,J"f(x)dx=A 曲边梯形面积 f(x)<0,["f(x)dx=-A 曲边梯形面积的负值 12 ∫f(x)dx=4-A+4-A4+4 各部分面积的代数和 HIGH EDUCATION PRESS 目录 返回 结
定积分的几何意义: f x f x x A b a ( ) 0, ( )d 曲边梯形面积 b a f (x) 0, f (x)dx 曲边梯形面积的负值 a b y x A1 A2 A3 A4 A5 1 2 3 4 5 f (x)d x A A A A A b a 各部分面积的代数和 A 机动 目录 上页 下页 返回 结束