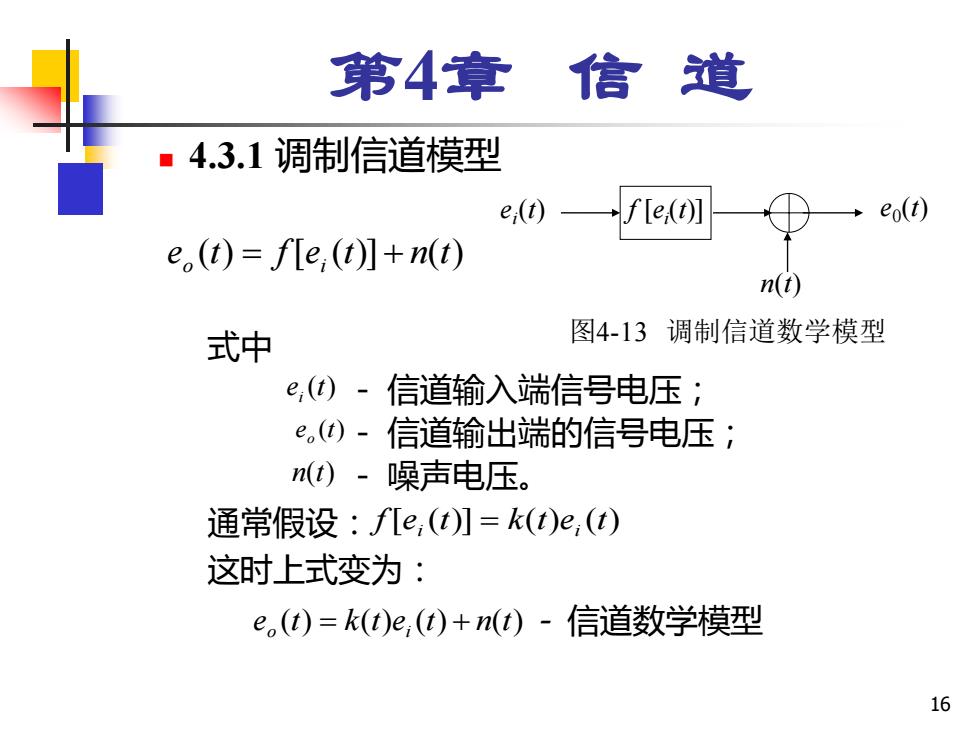
第4章信道 ■4.3.1调制信道模型 e,() fle(t)] eo(t) e(t)=f[e,(t)]+n(t) n(t) 式中 图4-13调制信道数学模型 e,(t)-信道输入端信号电压; e()-信道输出端的信号电压; n()-噪声电压。 通常假设:f[e,(t)]=k(t)e,(t) 这时上式变为: e(t)=k(t)e,(t)+n(t)-信道数学模型 16
16 第4章 信 道 ◼ 4.3.1 调制信道模型 式中 - 信道输入端信号电压; - 信道输出端的信号电压; - 噪声电压。 通常假设: 这时上式变为: - 信道数学模型 f [ei (t)] e0 e (t) i (t) n(t) 图4-13 调制信道数学模型 e (t) f[e (t)] n(t) o = i + e (t) i e (t) o n(t) f[e (t)] k(t)e (t) i = i e (t) k(t)e (t) n(t) o = i +

第4章信道 e,(t)=k(t)e;(t)+n(t) ◆因(t)随变,故信道称为时变信道。 ◆因k()与e;(t)相乘,故称其为乘性干扰。 ◆因)作随机变化,故又称信道为随参信道。 ◆若)变化很慢或很小,则称信道为恒参信道。 ◆乘性干扰特点:当没有信号时,没有乘性干扰。 17
17 第4章 信 道 ◆ 因k(t)随t变,故信道称为时变信道。 ◆ 因k(t)与e i (t)相乘,故称其为乘性干扰。 ◆ 因k(t)作随机变化,故又称信道为随参信道。 ◆ 若k(t)变化很慢或很小,则称信道为恒参信道。 ◆ 乘性干扰特点:当没有信号时,没有乘性干扰。 e (t) k(t)e (t) n(t) o = i +