
如果以样本方差对标准差进行无偏估计,则计算公式为: x- S=1回 (2.4.17) n-1 ⑤变异系数,表示了地理数据的相对变化(波动)程度,其计算公式: xn-1一×10% (2.4.18) 表24.5地理数据的离差 123456789101112 x128350355550724085296575 d-42.2528.75-425-19.250.75-42517.75-14.2530.75-26.2510.7520.75 例7对于表(24.5)中的数据,分别计算极差、离差、离差平方和、方差、标准差、 标准差的无偏估计,以及变异系数。具体的计算步骤如下: 按照公式(2.4.12)计算极差:R=73: 按照公式(2.4.13)计算离差平方和:d2=立d,=5666.25: 按照公式(2.41④计算方差:。=4=47219: 按照公式(2.4.15)计算标准差:6=√G2=√472.19=21.73: d2 按照公式(2416)计算标准差的无偏估计:S2一2270 按照公式(2.41)计算变异系:C-三x100%=04184; 2.4.3分布的偏度和峰度 (一)偏度系数测度地理数据分布的不对称性情况,刻画以平均值为中心的偏向情况, 计算公式为: (2.4.19y g1<0,表示负偏,即均值在峰值的左边:g1>0,表示正偏,即均值在蜂值的右边: g1-0,表示对称分布(如下图)
如果以样本方差对标准差进行无偏估计,则计算公式为: (2.4.17) 1 )( 1 S = i 2 − ∑ − = n xx n i ⑤变异系数,表示了地理数据的相对变化(波动)程度,其计算公式: %100 1 )( 1 %100 1 2 × − − =×= ∑= n xx x x S C n i i v (2.4.18) 表 2.4.5 地理数据的离差 1 2 3 4 5 6 7 8 9 10 11 12 xi 12 83 50 35 55 50 72 40 85 29 65 75 di -42.25 28.75 -4.25 -19.25 0.75 -4.25 17.75 -14.25 30.75 -25.25 10.75 20.75 例 7 对于表(2.4.5)中的数据,分别计算极差、离差、离差平方和、方差、标准差、 标准差的无偏估计,以及变异系数。具体的计算步骤如下: 按照公式(2.4.12)计算极差: R = 73; 按照公式(2.4.13)计算离差平方和: 25.5666 ; 12 1 2 = ∑ = i= dd i 按照公式(2.4.14)计算方差: 19.472 12 2 1 2 σ d == ; 按照公式(2.4.15)计算标准差: 73.2119.472 2 σσ === ; 按照公式(2.4.16)计算标准差的无偏估计: 70.22 112 2 = − = d S ; 按照公式(2.4.17)计算变异系: =×= 4184.0%100 x S Cv ; 2.4.3 分布的偏度和峰度 (一)偏度系数 测度地理数据分布的不对称性情况,刻画以平均值为中心的偏向情况, 计算公式为: (2.4.19) 3 1 1 1 ∑ ⎟ = ⎟ i g = σ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − n i xx n g1<0,表示负偏,即均值在峰值的左边;g1>0,表示正偏,即均值在峰值的右边; g1 =0,表示对称分布(如下图)
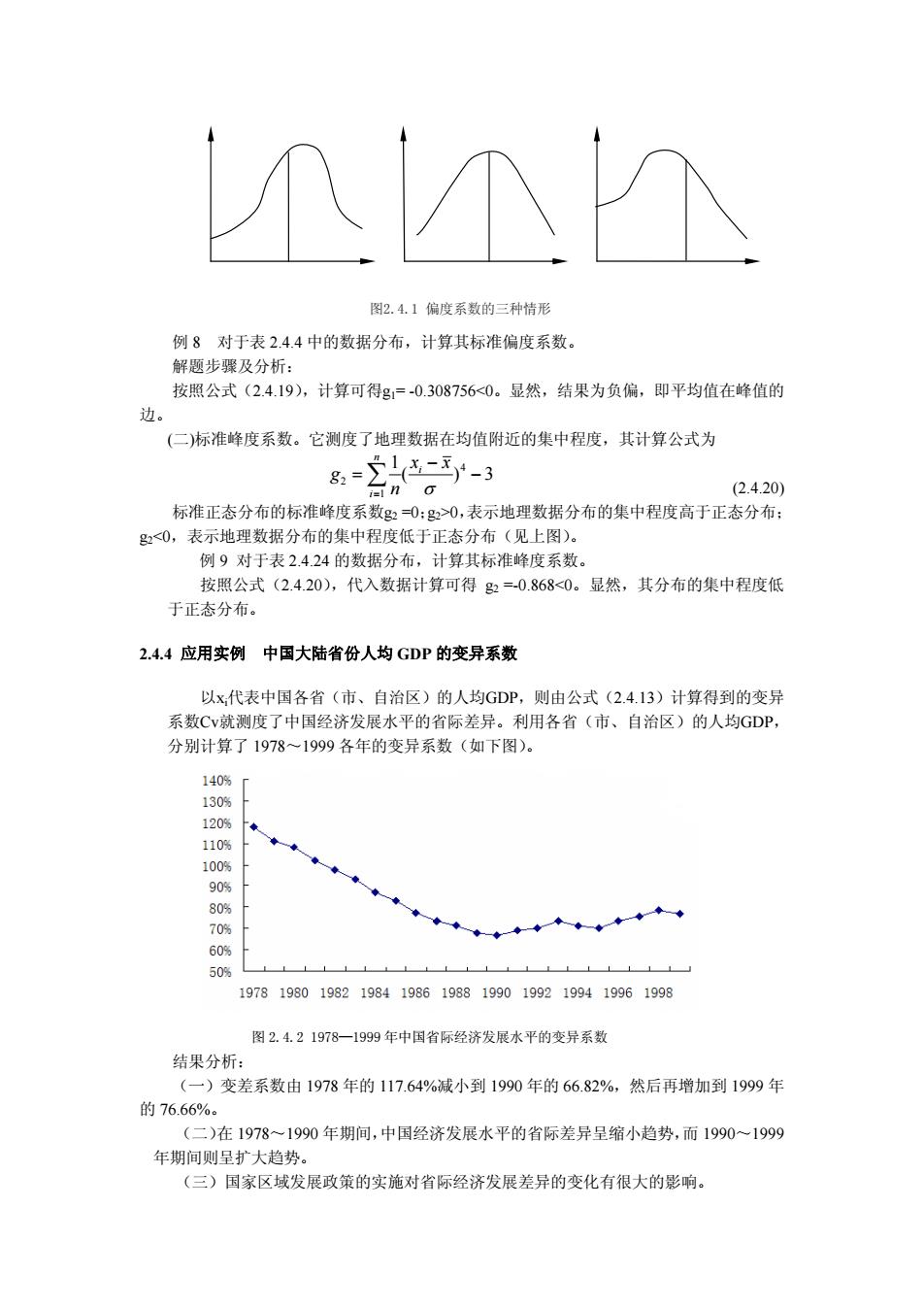
图2.4.1偏度系数的三种情形 例8对于表2.44中的数据分布,计算其标准偏度系数。 解题步骤及分析: 按照公式(2.4.19),计算可得g1=-0.308756<0。显然,结果为负偏,即平均值在峰值的 边。 (二)标准峰度系数。它测度了地理数据在均值附近的集中程度,其计算公式为 &2。-3 (2.420) 标准正态分布的标准峰度系数g2=0:2>0,表示地理数据分布的集中程度高于正态分布: g<0,表示地理数据分布的集中程度低于正态分布(见上图)。 例9对于表2.4.24的数据分布,计算其标准峰度系数。 按照公式(2.420),代入数据计算可得2=0.868<0。显然,其分布的集中程度低 于正态分布。 24.4应用实例中国大陆省份人均GDP的变异系数 以x代表中国各省(市、自治区)的人均GDP,则由公式(2.4.13)计算得到的变异 系数Cv就测度了中国经济发展水平的省际差异。利用各省(市、自治区)的人均GDP, 分别计算了1978~1999各年的变异系数(如下图)。 140% 130% 120% 110% 100% 90% 19781980198219841986198819901992199419961998 图2.4.21978一1999年中国省际经济发展水平的变异系数 结果分析 (一)变差系数由1978年的117.64%减小到1990年的66.82%,然后再增加到1999年 的76.66%。 (二)在1978~1990年期间,中国经济发展水平的省际差异呈缩小趋势,而1990~1999 年期间则早扩”大趋势。 (三)国家区域发展政策的实施对省际经济发展差异的变化有很大的影响
数据分布,计算其标准偏度系数。 照公式(2.4.19),计算可得g1= -0.308756<0。显然,结果为负偏,即平均值在峰值的 边。 )标准峰度 中程度高于正态分布; g2<0,表 2.4.20),代入数据计算可得 g2 =-0.868<0。显然,其分布的集中程度低 于正态分布。 2.4.4 应用实例 中国大陆省份人均 GDP 的变异系数 省(市、自治区)的人均GDP, 分别计算了 1978~1999 各年的变异系数(如下图)。 图2.4.1 偏度系数的三种情形 例 8 对于表 2.4.4 中的 解题步骤及分析: 按 (二 系数。它测度了地理数据在均值附近的集中程度,其计算公式为 (2.4.20) 标准正态分布的标准峰度系数g2 =0;g2>0,表示地理数据分布的集 3)( 4 − − = ∑ xx g 1 i 1 2 = n i n σ 示地理数据分布的集中程度低于正态分布(见上图)。 例 9 对于表 2.4.24 的数据分布,计算其标准峰度系数。 按照公式( 以xi代表中国各省(市、自治区)的人均GDP,则由公式(2.4.13)计算得到的变异 系数Cv就测度了中国经济发展水平的省际差异。利用各 图 2.4.2 1978—1999 年中国省际经济发展水平的变异系数 差系数由 1978 年的 117.64%减小到 1990 年的 66.82%,然后再增加到 1999 年 的 76 间,中国经济发展水平的省际差异呈缩小趋势,而 1990~1999 年期 (三)国家区域发展政策的实施对省际经济发展差异的变化有很大的影响。 结果分析: (一)变 .66%。 (二)在 1978~1990 年期 间则呈扩大趋势