
第章因子分析 §7.1因子分析的意义和作用 一、因子分析的概念和意义 因子分析是将多个实测变量转换为少数几个不相关的综合指标的多元统计方法,在教有 领域和若其它领域的科学研究中,往往需要对反映事物、现象从多个角度进行观测,也就设 计出多个观测变量,从多个变最收集大量数据以便进行分析寻找规律。多变量大样本虽然会 为我们的科学研究提供丰富的信息,但确幽加了据采集和处理的难府。更重要的是在大名 数情况下,许多变量之间存在 一定的相关关系,从而增加了问题分析的复杂性。 因子分析就是将大最的彼此可能存在相关关系的变最转换成较少的,彼此不相关的综合 指标的一种多元统计方法。这样既可减轻收集信息的工作量,且各综合指标代表的信息不重 叠。便于分析。 二、因子分析的基本过程 子分析的基本过程可分为两个步 第 步主因子分析 是通过原始变最的相关系数矩阵内部结构的研究,导出能控制所有变量的少数几个综合 变量,通过这少数几个综合变量去描述原始的多个变量之间的相关关系。一般来说,这少数 的几个综合变量是不可观测的,故称其为因子,我们又称这种通过原始变量相关系数矩阵出 发的因子分析为R型因子分析。因子分析所获得的反映变量间本质联系、变量与公共因子的 关系的全 部信息通过导 的因子负荷矩阵体现, 第二步对因子解释和命名 从因子分析导出的负荷矩阵的结构出发,把变量按与公共因子相关性大小的程度分组, 使同组内变量间的相关性较高,不同组的变量的相关性较低,按公因子包含变量的特点(即 公因子内涵)对因子作解释命名。 三、因子分析教材在分析测验中的作用 §7,2因子分析的原理和数学模型 一、数学模型(正交因子模型) 设m个可能存在相关关系的测试变量z,2,.,乙含有P个独立的公共因子 F,F2,F,(m≥p),测试变量z,含有独特因子孔,(i1m),诸,间互不相关,且与f,(j1.p) 也互不相关,每个z:可由P个公共因子和自身对应的独特因子线性表出: Z=a,E+a2E+.+aF。+cU1 Z2=aF+azF++aF+cU2 Z=amF+amF++ampFp+cUm (7.2-1) 用矩阵表示: (cU. =(di)x z. C.U
第 章 因子分析 §7.1 因子分析的意义和作用 一、因子分析的概念和意义 因子分析是将多个实测变量转换为少数几个不相关的综合指标的多元统计方法,在教育 领域和若其它领域的科学研究中,往往需要对反映事物、现象从多个角度进行观测,也就设 计出多个观测变量,从多个变量收集大量数据以便进行分析寻找规律。多变量大样本虽然会 为我们的科学研究提供丰富的信息,但确增加了数据采集和处理的难度。更重要的是在大多 数情况下,许多变量之间存在一定的相关关系,从而增加了问题分析的复杂性。 因子分析就是将大量的彼此可能存在相关关系的变量转换成较少的,彼此不相关的综合 指标的一种多元统计方法。这样既可减轻收集信息的工作量,且各综合指标代表的信息不重 叠。便于分析。 二、因子分析的基本过程 因子分析的基本过程可分为两个步骤: 第一步 主因子分析 是通过原始变量的相关系数矩阵内部结构的研究,导出能控制所有变量的少数几个综合 变量,通过这少数几个综合变量去描述原始的多个变量之间的相关关系。一般来说,这少数 的几个综合变量是不可观测的,故称其为因子,我们又称这种通过原始变量相关系数矩阵出 发的因子分析为 R 型因子分析。因子分析所获得的反映变量间本质联系、变量与公共因子的 关系的全部信息通过导出的因子负荷矩阵体现。 第二步 对因子解释和命名 从因子分析导出的负荷矩阵的结构出发,把变量按与公共因子相关性大小的程度分组, 使同组内变量间的相关性较高,不同组的变量的相关性较低,按公因子包含变量的特点(即 公因子内涵)对因子作解释命名。 三、因子分析教材在分析测验中的作用 §7.2 因子分析的原理和数学模型 一、数学模型(正交因子模型) 设m个可能存在相关关系的测试变量z1,z2, . . ,zm 含有P个独立的公共因子 F1,F2,.,Fp(m≥p),测试变量zi含有独特因子Ui(i=1.m),诸Ui间互不相关,且与Fj(j=1.p) 也互不相关,每个zi可由P个公共因子和自身对应的独特因子Ui线性表出: ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ++++= ++++= ++++= mm m mmpmp pp pp UcFaFaFaZ UcFaFaFaZ UcFaFaFaZ L LLLLLLLLLLLLLLL L L 2211 2221122 2 22 2121111 1 11 (7.2-1) 用矩阵表示: ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ × p mm pmij m Uc Uc Uc F F F a Z Z Z M M M 22 11 2 1 2 1 .)(
为 名46品巴 (7.12y 且满足:()P≤m (II)C0W(E.)=0(即F与U是不相关的) (III)E(F)=0 COV(F)=()=I 即F,.F,不相关,且方差皆为1,均值皆为0 (IV)E(心)=0C0V()=L。即U,.不相关,且都是标准化的变量,假定z,.,z。 也是标准化的,但并不相互独立。 式中A称为因子负荷矩陈,其元素(即(72-1)中久方程的系数)a:表示第i个恋品(2.)在 第个公共因子印,上的负荷,简称因子负荷,如果把2看成P维因子空间的一个向量,则a表 示Z:在坐标轴F,上的投影。 因子分析的目的就是通过模型(?.2-1)或(72-)'。以F代Z,由于一般有P<m,从而 大到简化弯量维数的愿望」 ,因子分析中的几个重要结论 因子分析数学处理的最后结果通常以因子负荷矩阵的形式给出,这个矩阵的一般形式如 下表所示。 因子负荷矩阵的一般格式 试 因子负荷量 变量 公共度(仙的 因子1 因子2 . 因子D 1 . a a 8-2 月. 龙-2 平方和 时-s=∑∑ 百分比B=S/m P:-/m Pr=Si/m p-si/m 根据对模型(7.2-1)(或(7.2-1)的假定(①) 一(IV)可以证明有如下结论 结论1因子负荷a是Z:与F的相关系数,C是Z与的相关系数,即aP5,C=P和 证明提示: 将(亿.2-1)的第i个方程两边乘以,并求期望,运用假设条件即得广P25
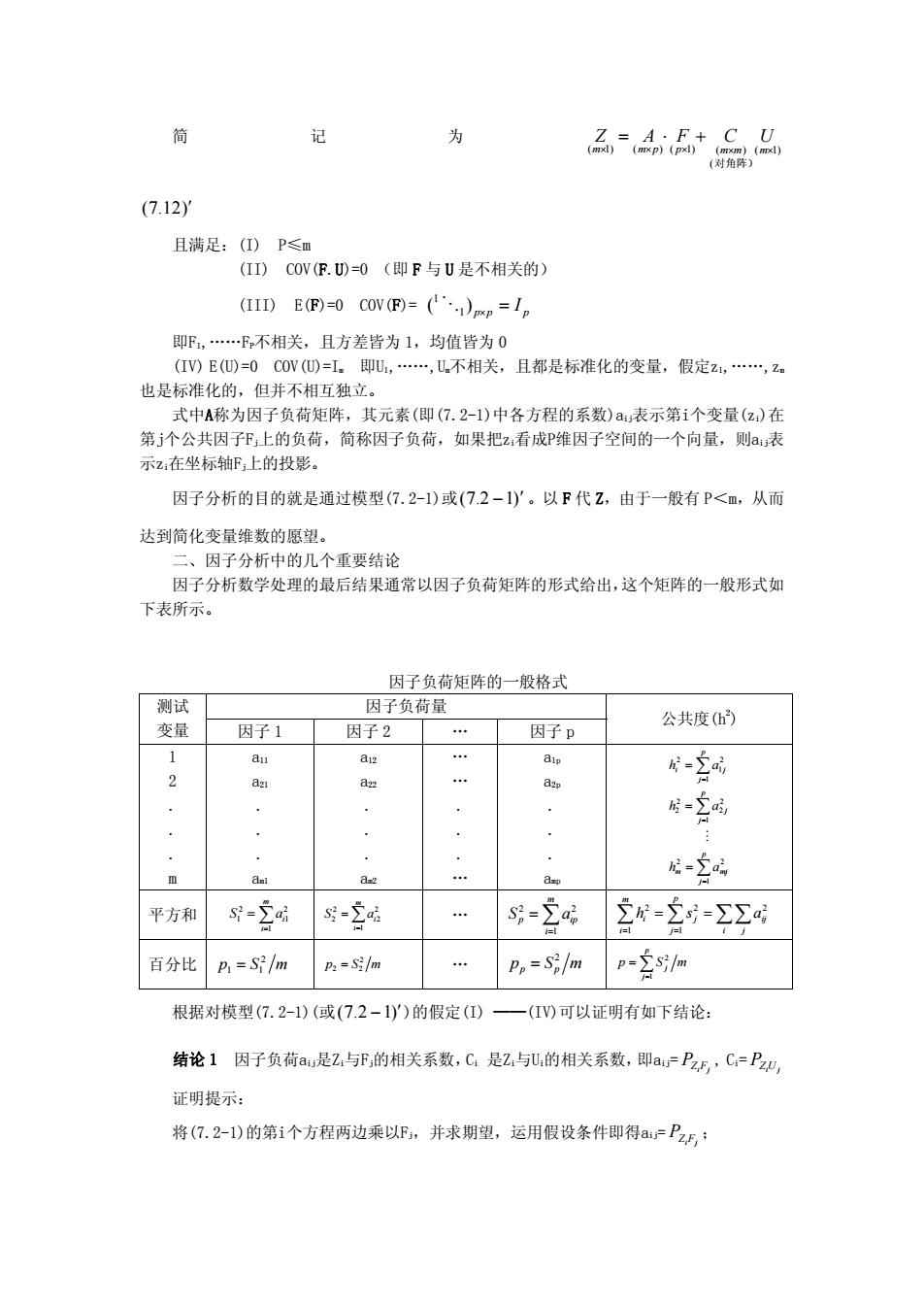
简记为 )1( ( ××× )1()()1( )( ×× = +⋅ ppmm mmm UCFAZ 对角阵) )12.7( ′ 且满足:(I) P≤m (II) COV(F.U)=0 (即 F 与 U 是不相关的) (III) E(F)=0 COV(F)= ppp = I × )( 1 1 O 即F1,.FP不相关,且方差皆为 1,均值皆为 0 (IV) E(U)=0 COV(U)=Im 即U1,.,Um不相关,且都是标准化的变量,假定z1,.,zm 也是标准化的,但并不相互独立。 式中A称为因子负荷矩阵,其元素(即(7.2-1)中各方程的系数)aij表示第i个变量(zi)在 第j个公共因子Fj上的负荷,简称因子负荷,如果把zi看成P维因子空间的一个向量,则aij表 示zi在坐标轴Fj上的投影。 因子分析的目的就是通过模型(7.2-1)或 − )12.7( ′ 。以 F 代 Z,由于一般有 P<m,从而 达到简化变量维数的愿望。 二、因子分析中的几个重要结论 因子分析数学处理的最后结果通常以因子负荷矩阵的形式给出,这个矩阵的一般形式如 下表所示。 因子负荷矩阵的一般格式 测试 因子负荷量 变量 因子 1 因子 2 . 因子 p 公共度(h2 ) 1 2 . . . m a11 a21 . . . am1 a12 a22 . . . am2 . . . . . . a1p a2p . . . amp ∑ ∑ ∑ = = = = = = p j m mj p j j p j i j ah ah ah 1 2 2 1 2 2 2 2 1 2 1 2 M 平方和 ∑= = m i i aS 1 2 1 2 1 ∑= = m i i aS 1 2 2 2 2 . ∑= = m i p aS ip 1 2 2 ∑∑ == ∑∑ = = i j ij p j j m i i ash 2 1 2 1 2 百分比 mSp 2 = 11 mSp 2 = 22 . pp mSp 2 = ∑= = p j j mSp 1 2 根据对模型(7.2-1)(或 − )12.7( ′ )的假定(I) ——(IV)可以证明有如下结论: 结论 1 因子负荷aij是Zi与Fj的相关系数,Ci 是Zi与Ui的相关系数,即aij= , C FZ ji P i= UZ ji P 证明提示: 将(7.2-1)的第i个方程两边乘以Fj,并求期望,运用假设条件即得aij= ; FZ ji P

将(亿.2-1)的第i个方程两边乘以,后求期望,由假设条件,可得C=P2 证明提示: 将(亿.2-1)中第1,j两个方程两边分别相乘后各取数学期望并利用假设条件可得结论。 结论3矩阵A中第1行平方和记为 好=立a店=1-c 证明提示: 将(7.2-1)中第1个方程两边自乘再各自求期望并运用假设条件可得。 结论4每个测试变量的方差由两部分组成: 1=D(Z,)=+c 证明提示: 对(?.2-1)第i个方程两边分别求方差并运用假设条件,我们称c为测试变量乙,的特殊 度,它表示2所含独特因子孔对忆方差所作的贡献。称为的共同度或公共度,它代表全 部公共因子对变量Z的方差所作的贡献,特别地表示第k个公共因子F对忆的方差所作的 贡献。越接近1,说明:的原始信息被所选P个公共因子解释得越好。例如:根据例1的 因子负荷阵(教材P162表7-2),h=0.932,表明2有93.2%的信息被三个公共因子说明了。 反之,当2靠近0时,说明公共因子对忆的解释很少,共信息主要由其独特因子U描述。 结论5A(a中,第列的平方和(,S-代表公共因子对所有 原始变量Z,Z,.,Z提供的方差贡献总和。 证:由前述a场的统计意义立得结论5。 由上可知:S是衡量公因子P相对重要性的指标。 百分比:S/2DZ)=S ×100%表示F,对所有测试变量的方差贡献率,其越大, m F,就越重要, 一般选择儿个公因子,就看所有公因子的方差贡献率之和(称为累计方差贡献 率)达到我们预想的百分比有儿个公因子· 以上是对正态因子模型导出的因子负荷矩阵作分析的全部依据,在实用中,我们得到的 仅是各Z的一个容量为的观测值,然后求出Z'=(亿,.,Z)的样本相关系数矩阵R用R估计
将(7.2-1)的第i个方程两边乘以Ui后求期望,由假设条件,可得Ci= UZ ii P 结论 2 ∑ (即z = = P K ZZ aaP jkik ji 1 i,zj的相关系数为矩阵A中第i,j两行向量之内积) 证明提示: 将(7.2-1)中第 i,j 两个方程两边分别相乘后各取数学期望并利用假设条件可得结论。 结论 3 矩阵 A 中 第 i 行平方和记为 2 1 2 2 1 i p k i ik ∑ −== cah = 证明提示: 将(7.2-1)中第 i 个方程两边自乘再各自求期望并运用假设条件可得。 结论 4 每个测试变量的方差由两部分组成: 22 )(1 iii +== chZD 证明提示: 对(7.2-1)第i个方程两边分别求方差并运用假设条件,我们称 为测试变量Z 2 i c i的特殊 度,它表示Zi所含独特因子Ui对Zi方差所作的贡献。称 为Z 2 hi i的共同度或公共度,它代表全 部公共因子对变量Zi的方差所作的贡献,特别地 表示第k个公共因子F 2 aik k对Zi的方差所作的 贡献。 越接近 1,说明Z 2 hi i的原始信息被所选P个公共因子解释得越好。例如:根据例 1 的 因子负荷阵(教材P162 表 7-2), 932.0 ,表明Z 2 h3 = 3有 93.2%的信息被三个公共因子说明了。 反之,当 靠近 0 时,说明公共因子对Z 2 hi i的解释很少,共信息主要由其独特因子Ui描述。 结论 5 A=(aij)中,第j列的平方和(j=1,.,p) ∑ 代表公共因子F = = m k j aS kj 1 2 2 j对所有 原始变量Z1,Z2,.,Zm提供的方差贡献总和。 证:由前述 的统计意义立得结论 5。 2 akj 由上可知: 是衡量公因子F 2 S j j相对重要性的指标。 百分比: %100)( 2 1 2 ∑ ×= = m S ZDS j m i j i 表示Fj对所有测试变量的方差贡献率,其越大, Fj就越重要,一般选择几个公因子,就看所有公因子的方差贡献率之和(称为累计方差贡献 率)达到我们预想的百分比有几个公因子。 以上是对正态因子模型导出的因子负荷矩阵作分析的全部依据,在实用中,我们得到的 仅是各Zi的一个容量为n的观测值,然后求出 Z′ =(Z1,.,Zm)的样本相关系数矩阵R用R估计

总体Z的相关系数,导出因子负荷阵,故称为R型因子分析。 §7.3公共因子的求解 要建立实际问题的因子模型,关键要根据样本数据估计因子负荷矩阵A,对A的估计方 法很多,这里仅介绍霍特林(但Hotelling)创立的,现使用较为普遍的主成份方法,(教材中 称为主因子法)。只介绍方法,不作论证。 一、因子分析从利试变量的样本相关矩陈出发 设对变量Z进行测试得容量为的观测值 21,22.,2m (i=1-m) 记, 脚%-2) 4-2- 称r为Z,Z的样本相关系数 1i.n 记R=(心)= 21123.2m 此为Z的 .0) 样本相关矩阵,是一个▣阶对称阵,再记对角阵C= 0G0.0 00.cm 其中C为模型(7.2-1)所示。 可以证明R与因子负荷阵A及C之间满足如下形式: R=A4+C2 1-c2 记R仁AA,则有RR-C 1-c2 1-c2 称R*为剩余相关矩阵,R*与R相比,仅主对角线上的元素不同,后者,主对角线全是1, 前者为1-c2=h 由于严格估计h存在困难,实际计算中有时忽略独特因子的作用,即取C:=0
总体Z的相关系数,导出因子负荷阵,故称为R型因子分析。 §7.3 公共因子的求解 要建立实际问题的因子模型,关键要根据样本数据估计因子负荷矩阵 A,对 A 的估计方 法很多,这里仅介绍霍特林(H.Hotelling)创立的,现使用较为普遍的主成份方法,(教材中 称为主因子法)。只介绍方法,不作论证。 一、因子分析从测试变量的样本相关矩阵出发。 设对变量Zi进行测试得容量为n的观测值 , )1( 21 zzz mi ii L in = — 记 jjii ij ij LL L r = 其中 ∑ ∑ ∑ = −= n k k jk k ij jkik ik zz n zzl 1 ))(( 1 ∑ ∑ = = −= n k k ii ik ik z n zl 1 2 1 2 )( 1 称rij为Zi,Zj的样本相关系数 记 此为 Z 的 mmm mm m m ij rrr rrr rrr rR × ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ == 1 1 1 )( 321 21 23 2 1312 1 L M L L 样本相关矩阵,是一个 m 阶对称阵,再记对角阵 ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = mc c c C KK KKKKK K KK 00 000 0 0 1 1 其中Ci为模型( −12.7 )所示。 可以证明 R 与因子负荷阵 A 及 C 之间满足如下形式: 2 = ′ + CAAR 记R*= AA′ ,则有 R*=R-C2 = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − − − 2 2 1 2 1 1 1 1 m ji ij c r c r c O 称 R*为剩余相关矩阵,R*与 R 相比,仅主对角线上的元素不同,后者,主对角线全是 1, 前者为 22 1 =− hc ii 由于严格估计 存在困难,实际计算中有时忽略独特因子的作用,即取C 2 hi i=0

(=1m),也就是令 R=AA'=(r) (7.3-3) 这里=∑00 上式就是求A的出发点,这种方法相当于预置h2=1,在此情况下提取主因子的方法称为 主分量分析,如预置的h2<1,则提取主因子的方法称为主因子分析 二、求主因子解的步骤 得到测试变量Z的样本相关矩阵R之后,求主因子解还需按以下几步进行。 1、求R的特征根,即解方程: 2-1-2.-m IE-R 1-1.-=0 rm1-r2.-l1 由R是非负定阵,解出的特征值都是非负的,将其非零特征值按从大到小排序并重新编码: 2、按预先规定所取的P个公共因子的累计方差贡献率达到的百分比(一般取85%) 使回 之085的P即为所取的公因子数(可以正明元,/∑元=三第k个公共因子的 2 方差贡献率)。 3、对选定的前P个特征值入,≥入2≥.≥入>0求相应的单位特征向量 4,巧. 为此求入,(1≤j≤p)的特征向量,即解方程组 (,-10x-i22-hmxm=0 x) (即(2,E-R):=0) -rm22.+(,-10xm=v (x 便得4,=(4,4,.4)) 再标准化便得 4、写出因子负荷阵
(i=1.m),也就是令 mmij = rAAR × = ′ )( (7.3-3) 这里 ∑= = n i ij aar jkik 1 上式就是求 A 的出发点,这种方法相当于预置 ,在此情况下提取主因子的方法称为 主分量分析,如预置的 ,则提取主因子的方法称为主因子分析。 1 2 hi = 1 2 hi < 二、求主因子解的步骤 得到测试变量 Z 的样本相关矩阵 R 之后,求主因子解还需按以下几步进行。 1、求 R 的特征根,即解方程: 0 1 1 1 || 1 2 21 2 12 1 = −− − −−− −− − =− λ λ λ λ K KKKK K K m m m m rr r r rr RE 由R是非负定阵,解出的特征值都是非负的,将其非零特征值按从大到小排序并重新编码: λ1≥λ2≥.0 2、按预先规定所取的 P 个公共因子的累计方差贡献率达到的百分比(一般取 85%) 使 85.0 1 1 ≥ ∑ ∑= m i p i i λ λ 的P即为所取的公因子数(可以证明 m sk m i k ∑ i = =1 λλ 第k个公共因子Fk的 方差贡献率)。 3、对选定的前P个特征值λ1≥λ2≥.≥λp>0 求相应的单位特征向量 oo LL o uuu p , 21 。 为此求λj(1≤j≤p)的特征向量uj,即解方程组: ⎪ ⎩ ⎪ ⎨ ⎧ =−+−− =−−−− xrxr vx xrxrx m m mj j mm )1( )1( 0 2211 2121 1 λ λ L LLLLLLLLLLLLL L ( = 0) ) ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ − m i j x x 即(λ RE M 便得 ),( 21 = ′ Luuuu mjjjj 再标准化便得 o u j 4、写出因子负荷阵