
第4节地理数据的统计描述与处理 在地理数据的分布性质中,最重要的两个性质是集中性和腐(分)散性。数据的集中性和 离散性可用平均指标和离散指标来表示。 2.4.1地理数据的平均指标 平均指标指同类社会经济现象在一定时间、地点条件下所达到的一般水平。平均指标是 数据描述中最基本的指标之一,具有具有代表性和抽象性的特点。 (一)平均指标的作用 (1)反映总体各变量分布的集中趋势和一般水平: (2)便于比较同类现象在不同单位间的发展水平 (3)能够比较同类现象在不同时间的发展变化趋势或规律: (4)分析现象之间的依存关系: (二)平均指标的分类 平均数根据其且体的代表意义和计算方式不同.可分为数值平均数和位置平均数 (1)数值平均数 数值平均数是对总体各单位某一标志值的平均 表明总体单位标志 值的一般水平。数值平均数包括算术平均数、调和平均数、几何平均数和幂平均数 ①算术平均数算数平均数按应用条件可分为简单算数平均数和加权算术平均数。 (a)简单算数平均数计算公式如下: (2.4.1) 式中,代表平均值,x(=1,2,m)代表未做统计分组的地理数据,n为样本数据。 应用条件未分组的地理数据,各组出现的次数都是1。 例15名学生的学习成绩分别为:75、91、64、53、82。则平均成绩为: 平均成绩=75+90+64+53+82%=365-73 5 (6)加权算术平均数计算公式如下: ∫ x=可 (2.4.2) 式中,x,=1,2,m)代表第1组的中值,如果第i组下限值为a,上限值为,上限值 为b,则x=a,=(亿-a,)/2:f代表第i组的频数,即出现在第i组的地理数据个数:m 为分组个数。 应用条件分组的地理数据,各组次数不同。 表2,41工人加工某种零件资料
第 4 节 地理数据的统计描述与处理 在地理数据的分布性质中,最重要的两个性质是集中性和离(分)散性。数据的集中性和 离散性可用平均指标和离散指标来表示。 2.4.1 地理数据的平均指标 平均指标指同类社会经济现象在一定时间、地点条件下所达到的一般水平。平均指标是 数据描述中最基本的指标之一,具有具有代表性和抽象性的特点。 (一)平均指标的作用 (1)反映总体各变量分布的集中趋势和一般水平; (2)便于比较同类现象在不同单位间的发展水平; (3)能够比较同类现象在不同时间的发展变化趋势或规律; (4)分析现象之间的依存关系; (二)平均指标的分类 平均数根据其具体的代表意义和计算方式不同,可分为数值平均数和位置平均数 (1)数值平均数 数值平均数是对总体各单位某一标志值的平均,表明总体单位标志 值的一般水平。数值平均数包括算术平均数、调和平均数、几何平均数和幂平均数。 ①算术平均数 算数平均数按应用条件可分为简单算数平均数和加权算术平均数。 (a)简单算数平均数 计算公式如下: ∑ (2.4.1) = = i x n i x n 1 1 式中, x 代表平均值, ( 1, 2, , i x i = L n) 代表未做统计分组的地理数据,n 为样本数据。 应用条件 未分组的地理数据,各组出现的次数都是 1。 例 1 5 名学生的学习成绩分别为:75、91、64、53、82。则平均成绩为: 平均成绩 73 5 365 5 = ++++ 8253649075 == (b)加权算术平均数 计算公式如下: ∑ (2.4.2) ∑ = = = m m i ii f xf x 1 i i 1 式中, ( 1, 2, , ) i x i m = L 代表第 组的中值,如果第 组下限值为 ,上限值为,上限值 为 ,则 ; i i i a i b ( )/ i i ii x a ba == − 2 i f 代表第 组的频数,即出现在第i 组的地理数据个数;m 为分组个数。 i 应用条件 分组的地理数据,各组次数不同。 表 2.4.1 工人加工某种零件资料

按日产量分组(件)x 工人数(人)£ 日产总量过 14 2 28 15 4 60 16 8 128 17 5 85 18 1 18 合计 20 319 平均日产量=39=16(件) 20 重要补充:权数起若对平均数的大小起者权衡轻重的作用。平均数总是趋向于出现次数 最多的那个标志值。权数的大小是直接通过各组单位数占总体单位数的比重来确定,也就是 频率的大小体现出来的。频率的大小就直接表明了该组标志值在平均数中占据的地位,频率 越大,该标志值计入平均数的份额也越大,对平均数的影响就越大:反之,频率越小,该标 志值计入平均数的份额就越小,对平均数的影响就越小,这就是权数权衡轻重作用的实质。 值得注意的一点是,当各组的次数都相同时,各标志值对平均数的影响都相同时,那就无所 谓权数的“权衡轻重”了。在这种情况下,加权算术平均数就等于简单算术平均数。 即当==.=n时,即 (2.4.3) ∑f时 可以说,简单算术平均数实际上是加权算术平均数的特例。 ②调和平均数调和平均数是社会经济统计中常用的另一种平均指标,它是根据标志值 的倒数计算的,所以又称倒数平均数。与算术平均数一样,调和平均数有简单调和平均数和 加权调和平均数两种。 (a)简单调和平均数计算公式如下: H 2.4.40 方安买 应用条件资料未分组,各个变量值次数都是1 例3 ,个 步行两里,走第一里时速度为每小时候10里,走第二里时为每小时20里, 则平均速度为:
按日产量分组(件)x 工人数(人)f 日产总量 xf 14 2 28 15 4 60 16 8 128 17 5 85 18 1 18 合计 20 319 例 2 某车间 20 名工人加工某种零件资料,根据表(2.4.1)计算加权算术平均数。 按公式(2.4.2)可得: 平均日产量 16 20 319 == (件) 重要补充:权数起着对平均数的大小起着权衡轻重的作用。平均数总是趋向于出现次数 最多的那个标志值。权数的大小是直接通过各组单位数占总体单位数的比重来确定,也就是 频率的大小体现出来的。频率的大小就直接表明了该组标志值在平均数中占据的地位,频率 越大,该标志值计入平均数的份额也越大,对平均数的影响就越大;反之,频率越小,该标 志值计入平均数的份额就越小,对平均数的影响就越小,这就是权数权衡轻重作用的实质。 值得注意的一点是,当各组的次数都相同时,各标志值对平均数的影响都相同时,那就无所 谓权数的“权衡轻重”了。 在这种情况下,加权算术平均数就等于简单算术平均数。 即当 1 2 . n f = == f f 时,即 1 1 1 n n i i i i i ii n i i 1 n x f fx x x nf n f = = = === ∑ ∑∑ ∑ = (2.4.3) 可以说,简单算术平均数实际上是加权算术平均数的特例。 ②调和平均数 调和平均数是社会经济统计中常用的另一种平均指标,它是根据标志值 的倒数计算的,所以又称倒数平均数。与算术平均数一样,调和平均数有简单调和平均数和 加权调和平均数两种。 (a)简单调和平均数 计算公式如下: 123 111 1 1 1 n n xx x x i i n n H = x = + + +⋅⋅⋅+ = ∑ (2.4.4) 应用条件 资料未分组,各个变量值次数都是 1。 例 3 一个人步行两里,走第一里时速度为每小时候 10 里,走第二里时为每小时 20 里, 则平均速度为:
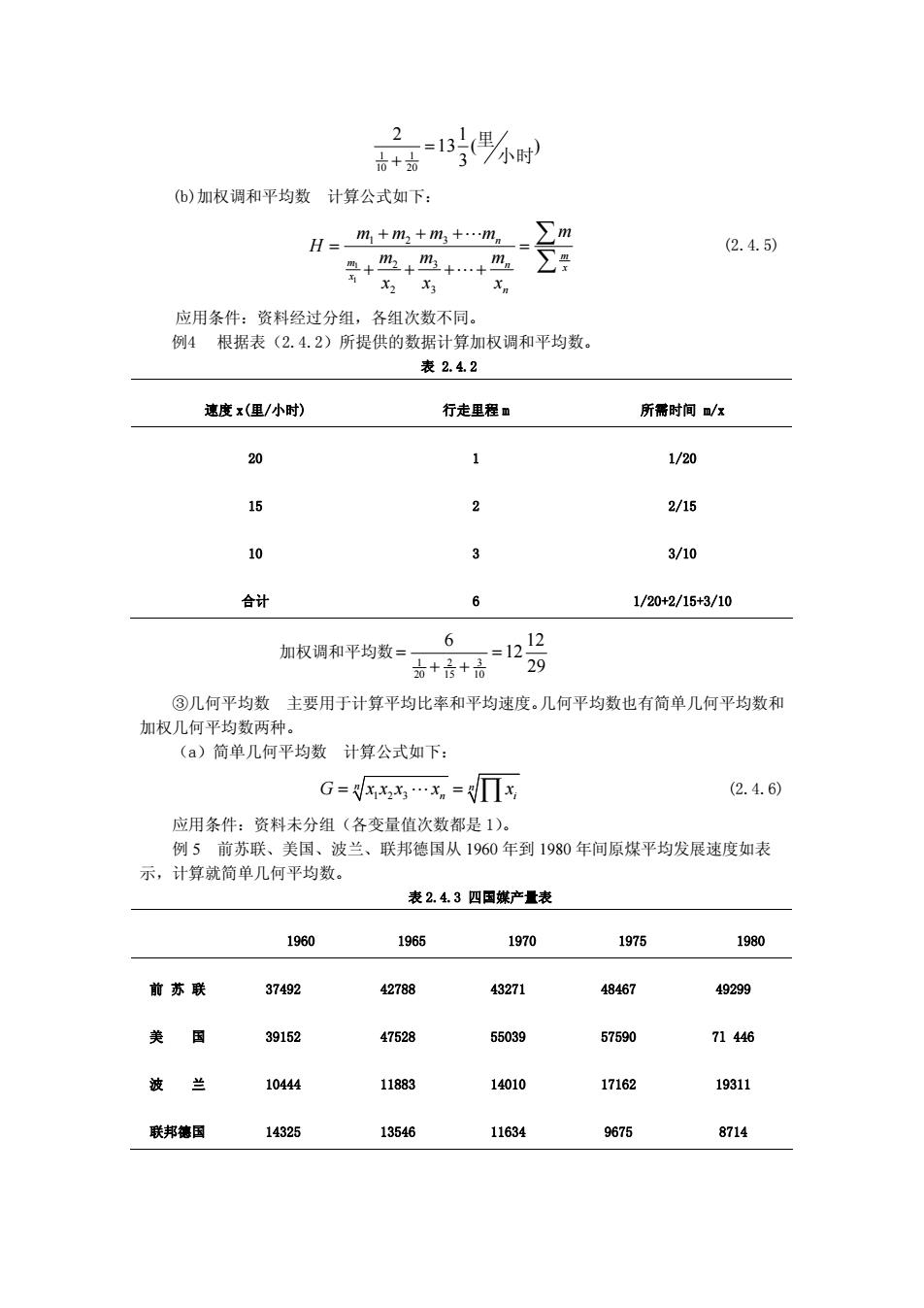
1时⅓时 2 ()加权调和平均数计算公式如下: H= m+m2+m3+.m。 (2.4.5) 应用条件:资料经过分组,各组次数不同 例4根据表(2.4.2)所提供的数据计算加权调和平均数。 表2.4.2 速度x(里/小时) 行走里程m 所需时间/x 20 1 1/20 15 2 2/15 白 3 3/10 合计 1/20+2/15+3/10 加权调和平均数= 号 6 ③几何平均数主要用于计算平均比率和平均速度。几何平均数也有简单几何平均数和 加权几何平均数两种 (a)简单几何平均数计算公式如下: G=x水.x=x (2.4.6) 应用条件:资料未分组(各变量值次数都是1)。 例5前苏联、美国、波兰、联邦德国从1960年到1980年间原煤平均发展速度如表 示,计算就简单几何平均数。 表2.43四国媒产量表 1960 1965 1970 1975 1980 前苏联37492 42788 43271 48467 49299 类国 39152 47528 5039 57590 71446 波兰 1044 11883 14010 17162 1931 联邦德国 14325 13546 11634 9675 8714
1 1 10 20 2 1 13 ( ) 3 = + 里小时 (b)加权调和平均数 计算公式如下: ∑ = ∑ +⋅⋅⋅+++ ⋅⋅⋅+++ = x m n n x m n m x m x m x m mmmm H 3 3 2 2 321 1 1 (2.4.5) 应用条件:资料经过分组,各组次数不同。 例4 根据表(2.4.2)所提供的数据计算加权调和平均数。 表 2.4.2 速度 x(里/小时) 行走里程 m 所需时间 m/x 20 1 1/20 15 2 2/15 10 3 3/10 合计 6 1/20+2/15+3/10 加权调和平均数 29 12 12 6 10 3 15 2 20 1 = ++ = ③几何平均数 主要用于计算平均比率和平均速度。几何平均数也有简单几何平均数和 加权几何平均数两种。 (a)简单几何平均数 计算公式如下: 123 n n G xxx x x = ⋅⋅⋅ = n ∏ i (2.4.6) 应用条件:资料未分组(各变量值次数都是 1)。 例 5 前苏联、美国、波兰、联邦德国从 1960 年到 1980 年间原煤平均发展速度如表 示,计算就简单几何平均数。 表 2.4.3 四国媒产量表 1960 1965 1970 1975 1980 前 苏 联 37492 42788 43271 48467 49299 美 国 39152 47528 55039 57590 7l 446 波 兰 10444 11883 14010 17162 19311 联邦德国 14325 13546 11634 9675 8714

49299 xg=37492 1.0138101.38% 19311 21044 -1.0312103.12% =0.975597.55% (b)加权几何平均数计算公式如下: (2.4.7) 应用条件资料经过分组,各组次数不同。 (2)位置平均数根据标志值某一特点位置来确定的平均数。它不是对统计数列中所有 各项数据进行计算所得的结果,而是根据数列中处于特殊位置上的个别单位或部分单位的标 志值来确定的.位晋平均新包括众数和中位数, ①众数 众数就是出现频数最多的那个数,计算方法分为以下两种情况 ()未分组的地理数据,可以根据每一个数据出现的频数大小直接确定众数。 (b)对于已经分组的地理数据,中位数的计算方法如下: 首先确定频数最多的组为众数所在组,再按以下公式计算众数: M。=L+d× △ (2.4.8) 1+△2 M。=U-d×A+A △、 (2.4.9) 上两式中,M。代表众数:L为众数所在组的下限值:U为众数所在组的上限值:△,为众数 组频数与下一组频数之差:△,为众数组频数与上一组频数之差:为众数所在组的组距。 ②中位数将各个数据从小到大排列,居于中间位置的那个数。 (a)对于未分组的地理数据,样本数n为奇数时,中位数是位置排在第(n+1)/2位的数 据:样本数为偶数时,中位数是排在中间位置的两个数据平均值。 (b)分组的地理数据,中位数的计算步骤为首先确定中位数所在的组位置,再按如下 公式计算中位数: =,泛-双 (2.4.10) 或 -2- (2.4.11) f
20 20 g 20 - 20 9755.0 97.55% 14325 8714 0312.1 103.12% 10444 19311 0305.1 103.05% 39152 71466 0138.1 101.38% 37492 49299 ٛٛ = = = = = − − g g x g χ χ χ (b)加权几何平均数 计算公式如下: 1 1 2 3 1 123 1 n n i i i n i f n f i f f f f n i G xxx x x = = = ∑ ∑ = ⋅⋅⋅ = f ∏ i (2.4.7) 应用条件 资料经过分组,各组次数不同。 (2)位置平均数 根据标志值某一特点位置来确定的平均数。它不是对统计数列中所有 各项数据进行计算所得的结果,而是根据数列中处于特殊位置上的个别单位或部分单位的标 志值来确定的.位置平均数包括众数和中位数。 ①众数 众数就是出现频数最多的那个数,计算方法 分为以下两种情况: (a)未分组的地理数据,可以根据每一个数据出现的频数大小直接确定众数。 (b)对于已经分组的地理数据,中位数的计算方法如下: 首先确定频数最多的组为众数所在组,再按以下公式计算众数: (2.4.8) 或 (2.4.9) 上两式中,M0 代表众数;L 为众数所在组的下限值;U 为众数所在组的上限值; 为众数 组频数与下一组频数之差; 为众数组频数与上一组频数之差;d 为众数所在组的组距。 Δ1 Δ2 ②中位数 将各个数据从小到大排列,居于中间位置的那个数 。 (a)对于未分组的地理数据,样本数 n 为奇数时,中位数是位置排在第(n+1)/2 位的数 据;样本数 n 为偶数时,中位数是排在中间位置的两个数据平均值。 (b)分组的地理数据,中位数的计算步骤为首先确定中位数所在的组位置,再按如下 公式计算中位数: 1 1 1 2 n i m i e m f S M Ld f − = − =+× ∑ (2.4.10) 或 m m n i i e f Sf dUM 1 2 1 1 + = − ×−= ∑ (2.4.11) 21 1 0 Δ M = dL ×+ Δ+Δ Δ 21 2 0 Δ+Δ M = dU ×−

上两式中,M代表中位数:L为中位数所在组的下限值。U为中位数所在组的上限值:∫。 为中位数所在组的频数:S,为中位数所在组以下的累计频数:S,为中位数所在组以上 的累计频数:d为中位数所在组的组距 例6下表(2.4.2)给出了某农场各农田地块的面积,试计算其中位数和众数。 表2.4.4某农场个农田地块的而积 地块编号12345 67 89101112平均值中位数众数 面积/hm12835035555072408529657554.2552.450 众数的计算先确定众数所在组。显然,众数所在的组应该在第二组。再按照公式 (2.4.8)计算众数=3476.19(元),或者按照公式(2.4.9)计算众数=3476.19(元)。 中位数的计算 先确定中数所在组的,因为,=1065所以中位应落在 二组。再按照(2.5.10)计算中位数Me=2588.46(元),或者按(2.4.11)计算中位数。 2.4.2地理数据的离散指标 前面说明了地理数据分布的集中性和一般水平,下面介绍地理数据分布的重要离散指 标。 (一)变异指标的含义变异指标是用来刻画总体分布的离散程度或变异状况,变异指 标越大,表明总体各单位标志值的变异程度越大。它是反映总体各标志值间差异程度的,且 能衡量总体平均数的代表性。常见的变异指标有极差、标准差、方差和变异系数。 (二)变异指标的作用 (1)用于衡量平均指标的代表性。 (2)反映社会经济活动的均衡 (3)研究总体标志值 布偏 正态的情况, ①极差极差是指所有数据中最大值与最小值之差。计算公式如下: R=max{x,)-min(x,) (2.4.12) 其优点是计算简便,缺点是易受极端值的影响。 ②离差离差是指每一个地理数据与平均值的差,计算公式如下: ③腐平方和高平方和是量一毛理数与平均值的离散程度。共计公 (9413 式如下: r=2x- (2.4.14) ④方差与标准差从平均概况衡量一组地理数据与平均值的离散程度。计算公式如下 2-123,-2 ni=l (2.4.15) 标准差为方差的平方根,计算公式如下: 2x- (2.4.16)
上两式中,Me 代表中位数;L 为中位数所在组的下限值。U 为中位数所在组的上限值; mf 为中位数所在组的频数; 为中位数所在组以下的累计频数; m 1 S − m 1 S + 为中位数所在组以上 的累计频数;d 为中位数所在组的组距 例 6 下表(2.4.2)给出了某农场各农田地块的面积,试计算其中位数和众数。 表 2.4.4 某农场个农田地块的面积 地块编号 1 2 3 4 5 6 7 8 9 10 11 12 平均值 中位数 众数 面积/hm2 12 83 50 35 55 50 72 40 85 29 65 75 54.25 52.4 50 众数的计算 先确定众数所在组。显然,众数所在的组应该在第二组。再按照公式 (2.4.8)计算众数M0 =3476.19 (元),或者按照公式(2.4.9)计算众数M0 =3476.19(元)。 中位数的计算 先确定中位数所在组的位置。因为, 7 1 1 1065 2 i i f = ∑ = 所以中位数应该落在第 二组。再按照(2.5.10)计算中位数 Me =2588.46(元),或者按(2.4.11)计算中位数。 2.4.2 地理数据的离散指标 前面说明了地理数据分布的集中性和一般水平,下面介绍地理数据分布的重要离散指 标。 (一)变异指标的含义 变异指标是用来刻画总体分布的离散程度或变异状况,变异指 标越大,表明总体各单位标志值的变异程度越大。它是反映总体各标志值间差异程度的,且 能衡量总体平均数的代表性。常见的变异指标有极差、标准差、方差和变异系数。 (二)变异指标的作用 (1)用于衡量平均指标的代表性。 (2)反映社会经济活动的均衡性。 (3)研究总体标志值分布偏离正态的情况。 ①极差 极差是指所有数据中最大值与最小值之差。计算公式如下: R i } (2.4.12) 其优点是计算简便,缺点是易受极端值的影响。 i i {min}{max i = − xx ②离差 离差是指每一个地理数据与平均值的差,计算公式如下: (2.4.13) ③离差平方和 离差平方和从总体上衡量一组地理数据与平均值的离散程度。其计算公 式如下: (2.4.14) ④方差与标准差 从平均概况衡量一组地理数据与平均值的离散程度。计算公式如下: (2.4.15) 标准差为方差的平方根,计算公式如下: (2.4.16) xd = xii − 2 1 = ) i d i 2 ∑( = − n xx ∑ = = − n i i xx n 1 ( 1 2) 2 σ ∑= = i − 2 σ ) n i xx n 1 ( 1