
静力学2、主矢和主矩力系中各力的矢量和。主矢R'=ZF主矩 M。=m +m, +m,+= mo(F)+ mo(F) +... = mo(F)大小: R'=~R?+R',= (zX)" +(zY)主矢R方向:平匠(移动效应)与简化中心位置无关[因主矢等于各力的矢量和]6
6 大小: 主矢 R 方向: R = Fi 主矢 ' = + + = = + + + ( ) ( ) ( ) 1 2 1 2 3 O O O i O m F m F m F M m m m 主矩 2 2 2 2 R' = R' +R' = ( X ) + (Y) x y − − = = X Y R R x y 1 1 tg tg (移动效应) 2、主矢和主矩 力系中各力的矢量和。 与简化中心位置无关 [因主矢等于各力的矢量和]

静力学大小:M。-mo(F)主矩M。转向:顺时针或逆时针(转动效应)与简化中心有关因主矩等于各力对简化中心取矩的代数和13、结论:平面一般力系向平面内一点简化可以得到一个力和一个力偶;该力作用在简化中心,大小和方向由力系的主矢决定:该力偶等于力系对简化中心的主矩4、应用实例:固定端(插入端)约束77771Z17277///7///7雨搭车刀
7 大小: 主矩MO 转向:顺时针或逆时针 与简化中心有关 (因主矩等于各力对简化中心取矩的代数和) ( ) MO =mO Fi (转动效应) 4、应用实例:固定端(插入端)约束 3、结论:平面一般力系向平面内一点简化可以得到一个力 和一个力偶;该力作用在简化中心,大小和方向由力系的 主矢决定;该力偶等于力系对简化中心的主矩。 雨 搭 车 刀
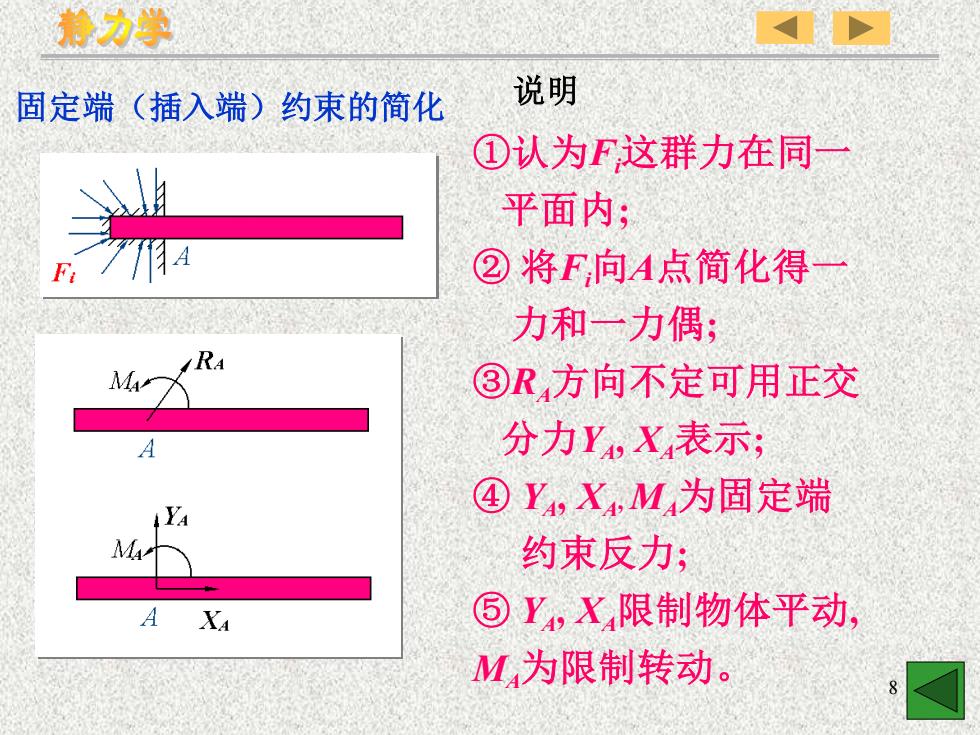
静力学说明固定端(插入端)约束的简化①认为F这群力在同一平面内;F/EA②将F向A点简化得力和一力偶;RA③R方向不定可用正交MA-分力Y,X表示:A④Y,X,M为固定端1YAM-+约束反力;③Y,X,限制物体平动,AXAM为限制转动
8 固定端(插入端)约束的简化 说明 ①认为Fi这群力在同一 平面内; ② 将Fi向A点简化得一 力和一力偶; ③RA方向不定可用正交 分力YA, XA表示; ④ YA , XA , MA为固定端 约束反力; ⑤ YA, XA限制物体平动, MA为限制转动

静力学$3-3平面任意力系的平衡条件与平衡方程由于=0 为力平衡Mo=0为力偶也平衡所以平面任意力系平衡的充要条件为力系的主矢B、和主矩M.都等于零,即:R'=N(ZX) +(EY)2 = 0M。-mo(F)=0
9 §3-3 平面任意力系的平衡条件与平衡方程 由于 =0 为力平衡 MO=0 为力偶也平衡 R 所以平面任意力系平衡的充要条件为: 力系的主矢 和主矩 MO 都等于零,即: ' ( ) ( ) 0 2 2 R = X + Y = MO =mO (Fi )=0 R

静力学平衡方程:ZmA(F)=0ZX=0ZX=0ZmB(F)= 0ZY=0ma(F)=0)Zmc(F)=0ZmB(F)=0mo(F)=0①一矩式②二矩式③三矩式条件:×轴不LAB条件:A,B,C不在连线同一直线上上式有三个独立方程,只能求出三个未知数。10
10 X = 0 mA (Fi ) = 0 mB (Fi ) = 0 ②二矩式 条件:x 轴不 AB 连线 ⊥ mA (Fi) = 0 mB (Fi) = 0 mC (Fi) = 0 ③三矩式 条件:A,B,C不在 同一直线上 上式有三个独立方程,只能求出三个未知数。 X = 0 Y =0 mO (Fi )=0 ①一矩式 平衡方程: