SCOAP测量范围 ▣可控制性-1(最容易) 一一无穷大(最困难) ▣可观察性-1(最容易)一一无穷大(最困难) ▣组合测量: ■大体上与电路连线数成正比,必须设置控制或观察 给定的连线. 口时序测量: ■大体上与触发器用来控制或观察给定的连线的时钟 个数#成正比。 2020/9/5 集成电路可测性设计 12
2020/9/5 集成电路可测性设计 12 SCOAP 测量范围 可控制性 – 1 (最容易) ——无穷大 (最困难) 可观察性 – 1 (最容易) ——无穷大 (最困难) 组合测量: 大体上与电路连线数成正比, 必须设置控制或观察 给定的连线. 时序测量: 大体上与触发器用来控制或观察给定的连线的时钟 个数# 成正比

5.1.1可控性值 ▣定义1:为了使电路中一内部节点N的值为0(1), 在电路中需要给节点赋以确定的值的最少赋值 次数之和--称为节点N的组合0(1)可控性值, 以CC0(N),CC1(N)表示. ▣定义2:为了使电路中一内部节点N的值为0(1), 在电路中必须置确定时序逻辑值的最少赋值次 数---称为节点N的时序0(1)可控性值,以 SC0N),SC1(N)表示. 2020/9/5 集成电路可测性设计 13
2020/9/5 集成电路可测性设计 13 5.1.1 可控性值 定义1: 为了使电路中一内部节点N的值为0(1), 在电路中需要给节点赋以确定的值的最少赋值 次数之和----称为节点N的组合0(1)可控性值, 以CC0(N), CC1(N)表示. 定义2: 为了使电路中一内部节点N的值为0(1), 在电路中必须置确定时序逻辑值的最少赋值次 数----称为节点N的时序0(1)可控性值, 以 SC0(N), SC1(N)表示

基本的逻辑单元的可控性值 口基本逻辑单元计算公式: ■若PI是原始输入,那么给I赋值只需给组合节点赋值一 次,而时序节点不需要赋值即可,因此有 >CCO(PI)=CCI(PI)=1 >SCO(PI)=SC1(PI)=0 ■对一缓冲器y=x,要确定y的值,那么y比x多一次组合节 点赋值,而缓冲器中无时序元件,因此有 >CC0(y)=CC0(x)+1 >CC1(y)=CC1(x)+1 >SCO(y)=SCO(x) >SC1(y)=SC1(x) ■非逻辑y=x >CC0(y)=CC(x)+1 >CC1(y)=CCO(x)+1 >SCo(y)=SCi(x) >SC1(y)=SCO(x) 2020/9/5 集成电路可测性设计 14
2020/9/5 集成电路可测性设计 14 基本逻辑单元计算公式: 若PI是原始输入, 那么给I赋值只需给组合节点赋值一 次, 而时序节点不需要赋值即可, 因此有 CC0(PI)= CC1(PI)=1 SC0(PI)= SC1(PI)=0 对一缓冲器y=x, 要确定y的值, 那么y比x多一次组合节 点赋值, 而缓冲器中无时序元件, 因此有 CC0(y)= CC0(x)+1 CC1(y)= CC1(x)+1 SC0(y)= SC0(x) SC1(y)= SC1(x) 非逻辑y=x CC0(y)= CC1(x)+1 CC1(y)= CC0(x)+1 SC0(y)= SC1(x) SC1(y)= SC0(x) 基本的逻辑单元的可控性值
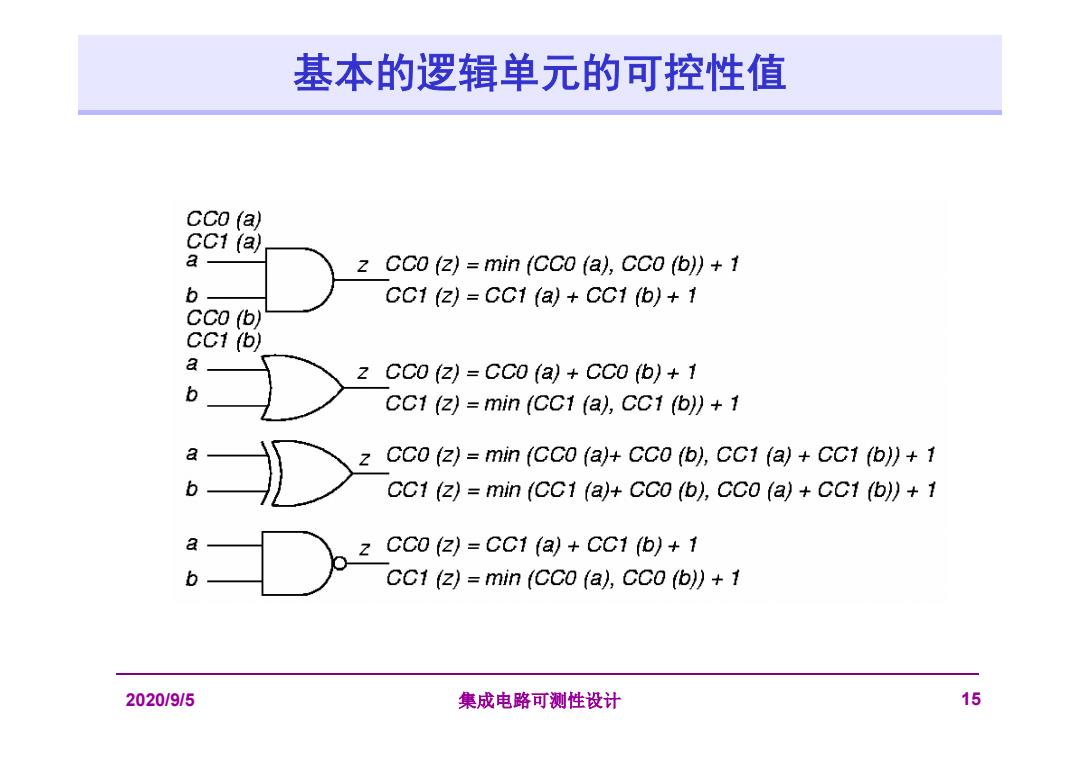
基本的逻辑单元的可控性值 CCo (a) 1(a) a z CCo (z)=min (CC0 (a),CCO (b))+1 b CC1 (z)=CC1 (a)+CC1 (b)+1 CCo(b) CC1 (b) a z CC0 (z)=CC0 (a)+CC0 (b)+1 b CC1 (z)=min (CC1 (a),CC1 (b))+1 a CCO (z)=min (CCO (a)+CC0 (b),CC1 (a)+CC1 (b))+1 b CC1 (z)=min (CC1 (a)+CC0 (b),CC0 (a)+CC1 (b))+1 CC0(2)=CC1(a+CC1(b)+1 CC1 (z)=min (CCO (a),CC0 (b))+1 2020/9/5 集成电路可测性设计 15
2020/9/5 集成电路可测性设计 15 基本的逻辑单元的可控性值
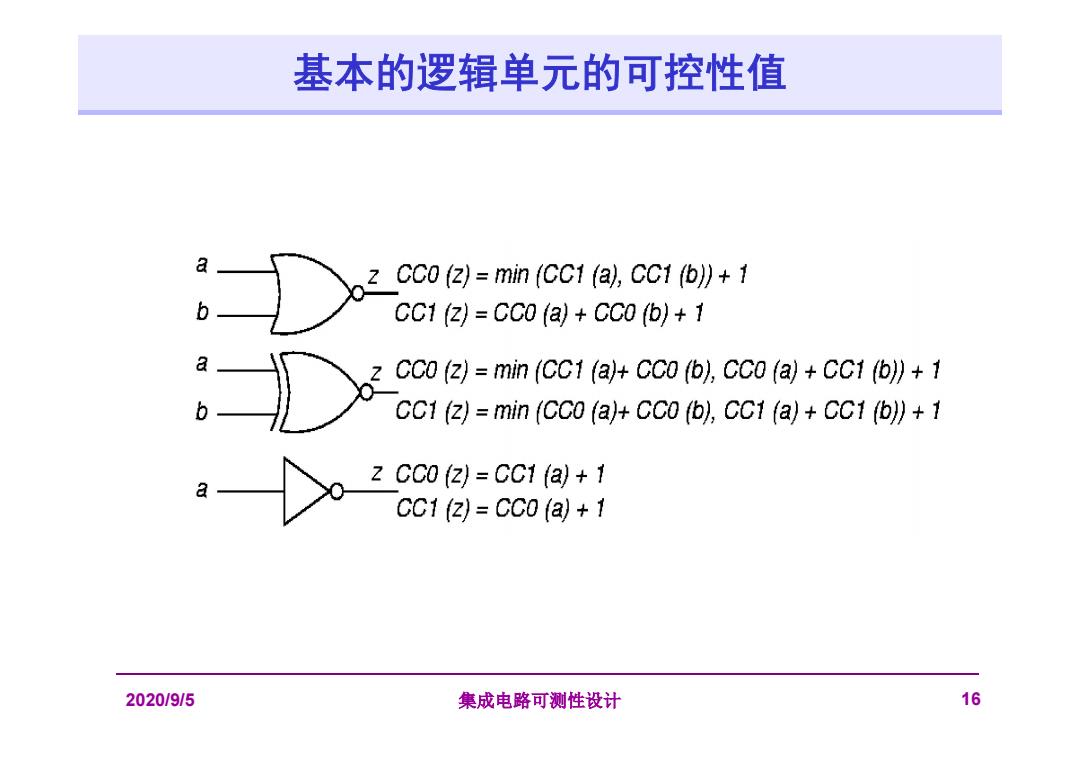
基本的逻辑单元的可控性值 z CC0 (z)=min (CC1 (a),CC1 (b))+1 CC1 (z)=CC0 (a)+CC0 (b)+1 Z CC0(亿)=min(CC1(a+CC0(b),CC0(a)+CC1b》+1 CC1 (z)min (CC0 (a)+CC0 (b),CC1 (a)+CC1 (b))+1 Z CC0 (Z)CC1 (a)+1 CC12)=CC0(a+1 2020/9/5 集成电路可测性设计 16
2020/9/5 集成电路可测性设计 16 基本的逻辑单元的可控性值