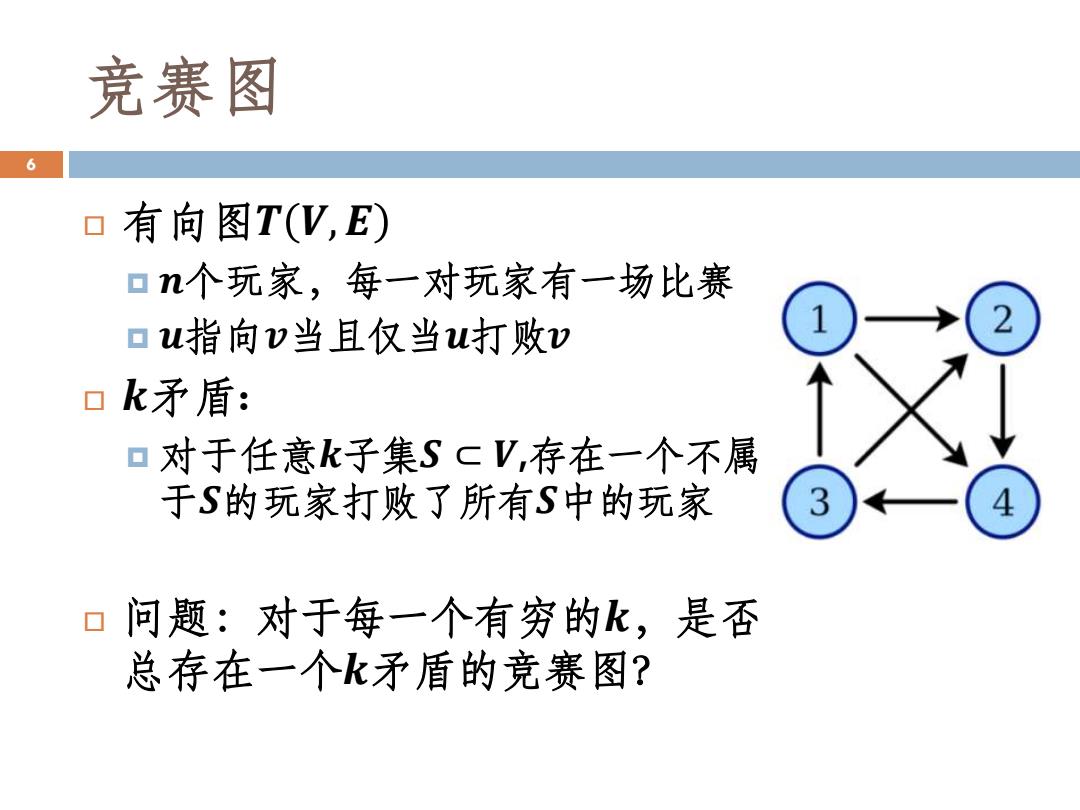
竞赛图 6 o有向图T(V,E) 口n个玩家,每一对玩家有一场比赛 口u指向v当且仅当u打败v 1 口k矛盾: 口对于任意k子集ScV,存在一个不属 于S的玩家打败了所有S中的玩家 3 口问题:对于每一个有穷的k,是否 总存在一个k矛盾的竞赛图?
竞赛图 有向图𝑻 𝑽,𝑬 𝒏个玩家,每一对玩家有一场比赛 𝒖指向𝒗当且仅当𝒖打败𝒗 𝒌矛盾: 对于任意𝒌子集𝑺 ⊂ 𝑽,存在一个不属 于𝑺的玩家打败了所有𝑺中的玩家 问题:对于每一个有穷的𝒌,是否 总存在一个𝒌矛盾的竞赛图? 6

飞矛盾的竞赛图的存在性 问:对任意有穷的k,是否总存在一个k矛盾的竞赛图? 定理(Erd6s1947) 若()(1-2-k)”-k <1,则存在n个节点的k矛盾的竞赛图. 证:随机取一个包含n个节点的竞赛图T(V,) 口对k子集S,令As:不存在V八S中玩家打败了S的所有玩家 P(A)=(1-2-k)n-k →P(U,A)≤∑Pay)=()(1-2)m-<1 →P(∩a)>0 即存在一个k矛盾的竞赛图
𝒌矛盾的竞赛图的存在性 问:对任意有穷的𝒌,是否总存在一个𝒌矛盾的竞赛图? 7 定理(Erdős 1947) 若 𝒏 𝒌 𝟏 − 𝟐 −𝒌 𝒏−𝒌 < 𝟏,则存在𝒏个节点的𝒌矛盾的竞赛图. 证:随机取一个包含𝒏个节点的竞赛图𝑻 𝑽,𝑬 对𝒌子集𝑺,令𝑨𝑺 :不存在𝑽\𝐒中玩家打败了𝑺的所有玩家 𝑷 𝑨𝑺 = 𝟏 − 𝟐 −𝒌 𝒏−𝒌 ⟹ 𝑷 ራ𝑺 𝑨𝑺 ≤ 𝑺 𝑷 𝑨𝑺 = 𝒏 𝒌 𝟏 − 𝟐 −𝒌 𝒏−𝒌 < 𝟏 ⟹ 𝑷 ሩ𝑺 𝑨𝒔 > 𝟎 即存在一个𝒌矛盾的竞赛图
期望论证 8 若班级学生的平均身高为L,则存在一个同学其 身高≥I(≤). max avg min 市 口对随机变量X,设E[X]= ▣P(X≥)>0 ▣P(X≤)>0
期望论证 若班级学生的平均身高为𝒍,则存在一个同学其 身高≥ 𝒍 (≤ 𝒍). 对随机变量𝑿,设𝑬 𝑿 = 𝝁 𝑷 𝑿 ≥ 𝝁 > 𝟎 𝑷 𝑿 ≤ 𝝁 > 𝟎 8
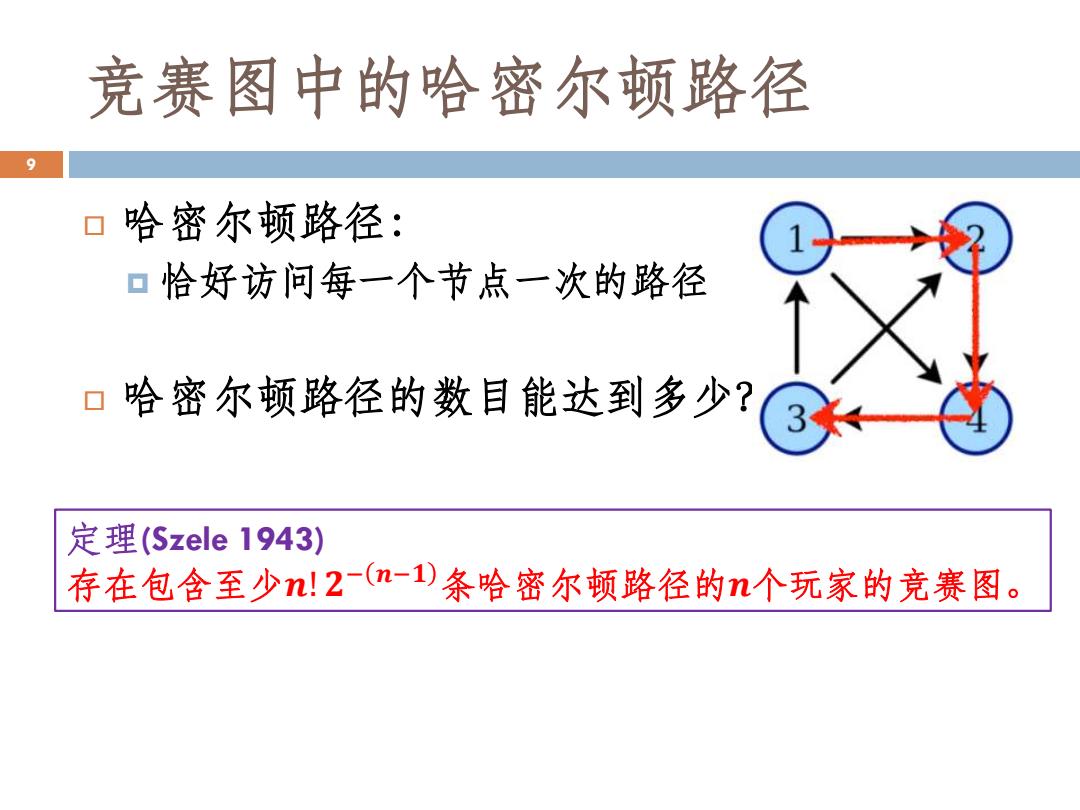
竞赛图中的哈密尔顿路径 9 口哈密尔顿路径: 口恰好访问每一个节点一次的路径 口哈密尔顿路径的数目能达到多少? 定理(Szele1943) 存在包含至少n!2(n-1D条哈密尔顿路径的n个玩家的竞赛图
竞赛图中的哈密尔顿路径 哈密尔顿路径: 恰好访问每一个节点一次的路径 哈密尔顿路径的数目能达到多少? 9 定理(Szele 1943) 存在包含至少𝒏! 𝟐 − 𝒏−𝟏 条哈密尔顿路径的𝒏个玩家的竞赛图

竞赛图中的哈密尔顿路径 10 定理(Szele1943) 存在包含至少n!2(n-1D条哈密尔顿路径的n个玩家的竞赛图。 口随机选取定义在n个玩家上的竞赛图T([n],E) 令X表示T中包含的哈密尔顿路径数目 ▣考虑[n]的置换π,定义 1 X元= π是哈密尔顿路径 π不是哈密尔顿路径 E[X元]=P(Xm=1)=2-(n-1) Ex=∑Exxl=2-m-)
竞赛图中的哈密尔顿路径 随机选取定义在𝒏个玩家上的竞赛图𝑻 [𝒏],𝑬 令𝑿表示𝑻中包含的哈密尔顿路径数目 考虑[𝒏]的置换𝝅,定义 𝑿𝝅 = ቊ 𝟏 𝝅是哈密尔顿路径 𝟎 𝝅不是哈密尔顿路径 𝑬 𝑿𝝅 = 𝑷 𝑿𝝅 = 𝟏 = 𝟐 − 𝒏−𝟏 𝑬 𝑿 = 𝝅 𝑬 𝑿𝝅 = 𝒏! 𝟐 − 𝒏−𝟏 10 定理(Szele 1943) 存在包含至少𝒏! 𝟐 − 𝒏−𝟏 条哈密尔顿路径的𝒏个玩家的竞赛图