
上式表明:>随着颗粒向下沉降,u逐渐增大,du/de逐渐减少。>当u增到一定数值u,时,du/de=0。颗粒开始作匀速沉降运动颗粒的沉降过程分为两个阶段:>加速阶段;>匀速阶段。沉降速度(terminalvelocity):也称为终端速度,匀速阶段颗粒相对于流体的运动速度。当du/de=0时,令u=u,则可得沉降速度计算式4gd,(p,-p)35p
¾ 随着颗粒向下沉降,u逐渐增大,du/dθ 逐渐减少。 ¾ 当u增到一定数值ui时,du/dθ =0。颗粒开始作匀速沉降运动。 ζρ ρρ 3 − )(4 = pp t gd u 当du/dθ =0时,令u= ut,则可得沉降速度计算式 上式表明: 颗粒的沉降过程分为两个阶段: 沉降速度(terminal velocity) :也称为终端速度,匀速阶段颗 粒相对于流体的运动速度。 ¾加速阶段; ¾匀速阶段
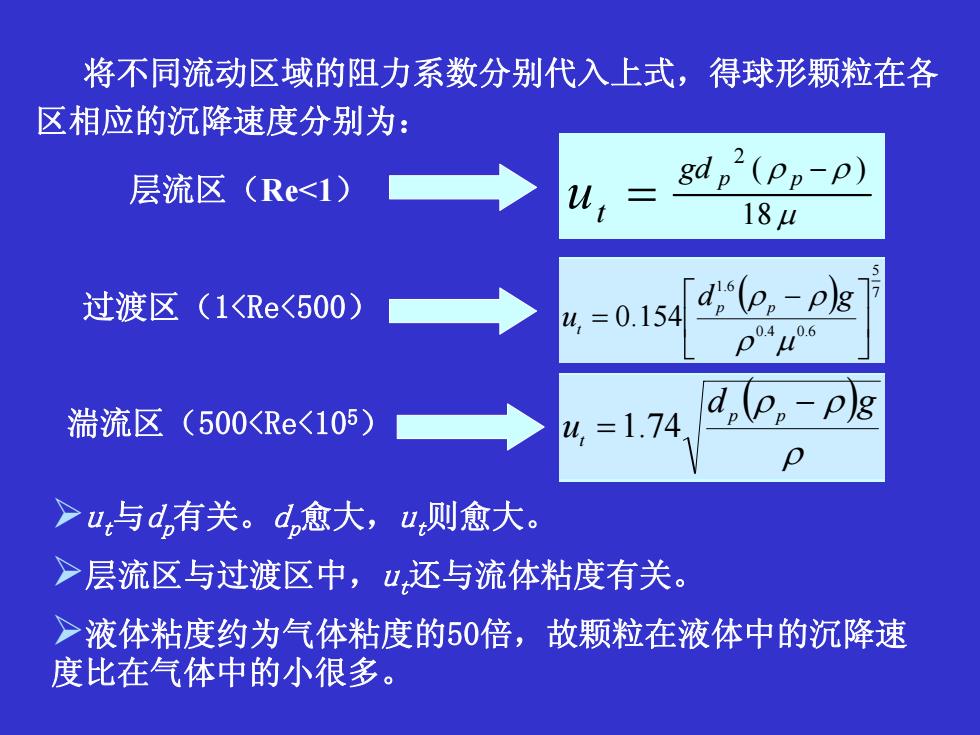
将不同流动区域的阻力系数分别代入上式,得球形颗粒在各区相应的沉降速度分别为:p-p)gd层流区(Re<1)U18 μd, (e, - p)g过渡区(1<Re<500)u=0.154p04u0.6d,(p,-p)g瑞流区(500<Re<105)u,=1.74O>ut与d有关。d愈大,u则愈大。层流区与过渡区中,u还与流体粘度有关。液体粘度约为气体粘度的50倍,故颗粒在液体中的沉降速度比在气体中的小很多
将不同流动区域的阻力系数分别代入上式,得球形颗粒在各 区相应的沉降速度分别为: 层流区(Re<1 ) μ ρρ 18 )( 2 − = pp gd u t p p t d g u 3 1 2 2 225 )(4 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − = μρ ρρ ρ ρρ dg pp u t − )(3 = 过渡区(1<Re<500) 湍流区(500<Re<10 5 ) ¾ ut与 dp有关。 dp愈大, ut则愈大。 ¾层流区与过渡区中, ut还与流体粘度有关。 ¾液体粘度约为气体粘度的50倍,故颗粒在液体中的沉降速 度比在气体中的小很多。 ( ) 7 5 6.04.0 6.1 154.0 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = μρ d ρρ g u pp t ( ) ρ ρρ gd u pp t − = 74.1

沉降速度的求法:求沉降速度通常采用试差法。①假设流体流动类型;②计算沉降速度;③计算Re,验证与假设是否相符;④如果不相符,则转①。如果相符,OK!图解法.(即摩擦因素群法)285页
①假设流体流动类型; ②计算沉降速度; ③计算Re,验证与假设是否相符; ④如果不相符,则转①。如果相符,OK ! 求沉降速度通常采用试差法。 沉降速度的求法: 图解法.(即摩擦因素群法) 285页
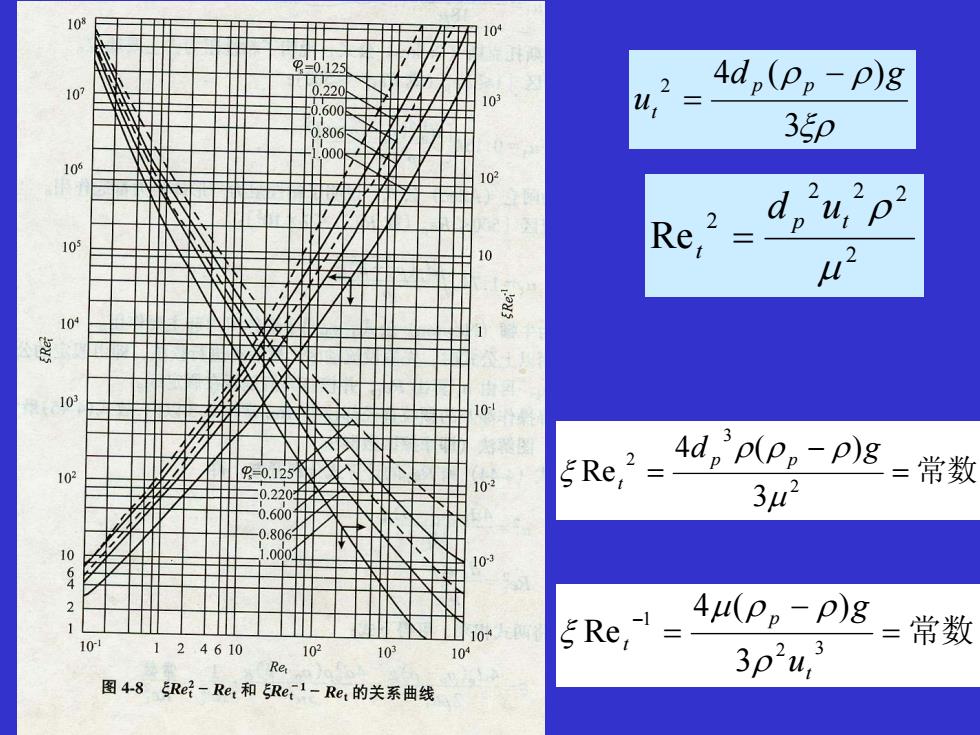
4d,(p,-p)g1073p10CA2Re10u1010304d,p(p,-p)g=常数ERe,21033μ21064μ(pp-p)g=常数ERe,110-112461010210103p"u,Re图4-8ERe-Re和ERe-1-Re,的关系曲线
= 常数 − = 2 3 2 3 )(4 Re μ ρρρ ξ d g pp t = 常数 − = − 2 3 1 3 )(4 Re t p t u g ρ μ ρ ρ ξ ξρ ρ ρ 3 )(4 2 d g u pp t − = 2 22 2 2 Re μ tp ρ t ud =

例:计算直径为95um,密度为3000kg/m3的固体颗粒分别在20℃的空气和水中的自由沉降速度。解:在20℃的水中:20℃水的密度为998.2kg/m3,粘度为1.005×10-3Pa·s先设为层流区。d2(pp-p)g_ (98x10-6)x(000-998.2)x9.81= 9.797×10-3 m / s18m18x1.005x10-3计算Re,核算流型:d,up95x10x9.79710x9982=0.9244<1Re:1.005x10-3u假设正确,计算有效。例题4-1,4-2
例:计算直径为95 μm,密度为3000kg/m 3的固体颗粒 分别在20 ℃的空气和水中的自由沉降速度。 u sm d g t pp /10797.9 3 10005.118 81.9)2.9983000()1098( 18 )( 3 6 2 − ×× − ×−×× = = − ×= − μ ρρ 计算Re,核算流型: Re 3 19244.0 6 3 10005.1 2.99810797.91095 == − <= − − × ×××× μ pud ρ 假设正确,计算有效。 解:在20 ℃的水中: 20 ℃水的密度为998.2kg/m 3,粘度为 1.005×10-3 Pa⋅s 先设为层流区。 例题4-1,4-2