
颗粒所受的阻力F,可用下式计算pu2up =d(Re) = Φu流体密度:流体粘度;颗粒的当量直径;颗粒在运动方向上的投影面积;颗粒与流体相对运动速度。阻力系数,是雷诺数Re的函数,由实验确定
ρ——流体密度; μ—— 流体粘度; dp——颗粒的当量直径; A—— 颗粒在运动方向上的投影面积; u—— 颗粒与流体相对运动速度。 ξ —— 阻力系数,是雷诺数Re的函数,由实验确定。 2 2 u d AF ρ = ζ 颗粒所受的阻力Fd可用下式计算 )((Re) μ ρ φφζ ud p ==

阻力系数:反应颗粒运动时流体对颗粒电力。通过因次分析可知,阻力系数是颗粒与流体相对运动时雷诺准数的函数。如图4-6。由图看出,球形颗粒的曲线按雷诺准数值大致分为三个区,各区内的曲线可分别用相应的关系式表达5= 24 / Re>层流区(斯托克斯Stokes区,10-4<Re<1)5 = 18.5/Re, 0.6>过渡区(艾仑A11en区,1<Re<103)= 0.44>流区(牛顿Newton区,103<Re<105)>边界层内为流区(Re>2*105)注意:其中斯托克斯区的计算式是准确的,其它两个区域的计算式是近似的
ζ = Re/24 t ζ = 44.0 ¾层流区(斯托克斯Stokes区,10-4<Re<1) 阻力系数:反应颗粒运动时流体对颗粒曳力。 通过因次分析可知,阻力系数是颗粒与流体相对运动时雷诺准 数的函数。如图4-6。由图看出,球形颗粒的曲线按雷诺准数 值大致分为三个区,各区内的曲线可分别用相应的关系式表 达。 注意:其中斯托克斯区的计算式是准确的,其它两个区域 的计算式是近似的。 ¾过渡区(艾仑Allen区,1<Re<103) ¾湍流区(牛顿Newton区,103<Re<105) ¾边界层内为湍流区(Re>2*105) 6.0 ζ = Re5.18 t ζ = 1.0
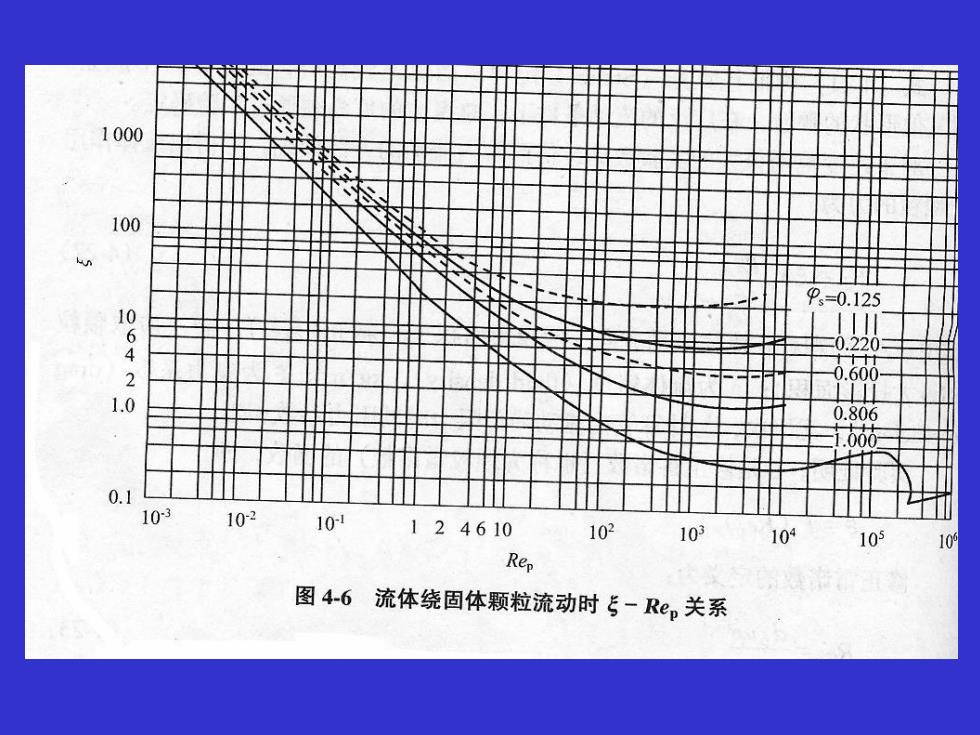
10001003s=0.12510640.60021.00.8061.0000.110-310-210-112461010210310410510Rep图4-6流体绕固体颗粒流动时-Re,关系

二、重力沉降重力沉降(gravitysettling):由地球引力作用而发生的颗粒沉降过程,称为重力沉降1沉降速度1.1球形颗粒的自由沉降自由沉降(freesettling):单个颗粒在流体中沉降,或者颗粒群在流体中分散得较好而颗粒之间互不接触互不碰撞的条件下沉降
自由沉降(free settling): 单个颗粒在流体中沉降,或 者颗粒群在流体中分散得较好而颗粒之间互不接触互不碰撞的 条件下沉降。 二、重力沉降 重力沉降(gravity settling):由地球引力作用而 发生的颗粒沉降过程,称为重力沉降。 1 沉降速度 1.1 球形颗粒的自由沉降
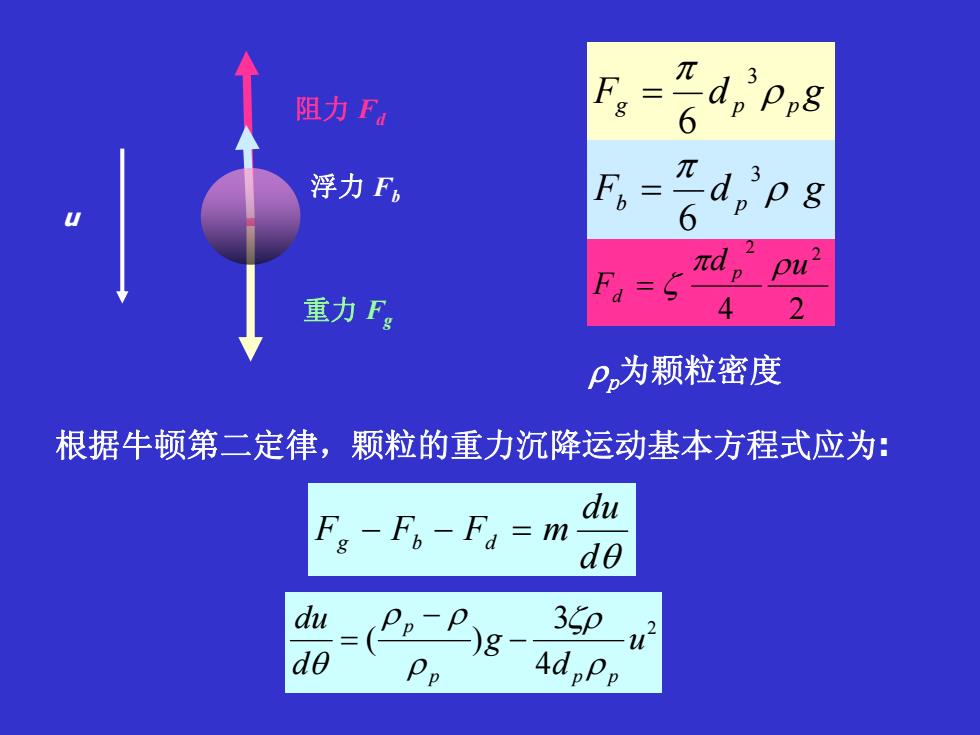
元D8阻力Fa6元浮力Fg6元dpu4重力FgP,为颗粒密度根据牛顿第二定律,颗粒的重力沉降运动基本方程式应为:duF-F-F=m2dedude4d.ppp
dθ du dbg =−− mFFF 2 4 3 )( u d g ddu p pp p ρ ζρ ρ ρ ρ θ − − = 根据牛顿第二定律,颗粒的重力沉降运动基本方程式应为: u 重力 Fg 阻力 Fd 浮力 Fb 24 2 2 d u F p d π ρ = ζ g ρ pp gdF π 3 6 = b p ρ gdF π 3 6 = ρp为颗粒密度