
课前导读 1,1 1+2+3+4+.+n+.=? 1+2+2交+.+ +.=7 我们可以把项和取极限,作为无穷多项相加的和,则可以得到: 1+2+3+4+.+n+.=lim n(n+1) =00 n-→0 +.1+.+1 1+ 十 2+.=lim 2 2 2 第一个极限不存在,因此“和“不存在;第二个极限存在,因此“和 为2.这就是我们要研究的无限项和的问题,即级数的收敛问题
课 前 导 读 1 2 3 4 ? + + + + + + = n 2 1 1 1 1 ? 2 2 2n + + + + + = 我们可以把n项和取极限,作为无穷多项相加的和,则可以得到: ( 1) 1 2 3 4 lim n 2 n n n → + + + + + + + = = ; 2 1 1 1 1 1 1 2 1 lim 2 2 2 2 1 2 n n n→ − + + + + + = = . 第一个极限不存在,因此“和”不存在;第二个极限存在,因此“和” 为 2. 这就是我们要研究的无限项和的问题,即级数的收敛问题
一常数项级数的概念 第八章无穷级数 人们认识事物在数量方面的特性,往往有一个由近似到精确的过程在这种 认识过程中,会遇到由有限个数量相加到无穷多个数量相加的问题
第八章 无穷级数 人们认识事物在数量方面的特性,往往有一个由近似到精确的过程.在这种 认识过程中,会遇到由有限个数量相加到无穷多个数量相加的问题. 一、常数项级数的概念 R

常数项级数的概念 第八章无穷级数 定义1设有数列{un}(n=1,2,),将数列(n=1,2,{4n}中的各项用加号 连接的形式 41+山2+.+4n+. 称为常数项无穷级数,简称级数,记为∑4,其中工是求和符号,称为级数的 一般项(通项)
第八章 无穷级数 定义 1 设有数列un (n =1,2, ) ,将数列(n =1,2, ) un 中的各项用加号 连接的形式 1 2 n u u u + + + + 称为常数项无穷级数,简称级数,记为 1 n n u = , 一、常数项级数的概念 其 中 是求和符号, n u 称为级数的 一般项(通项)
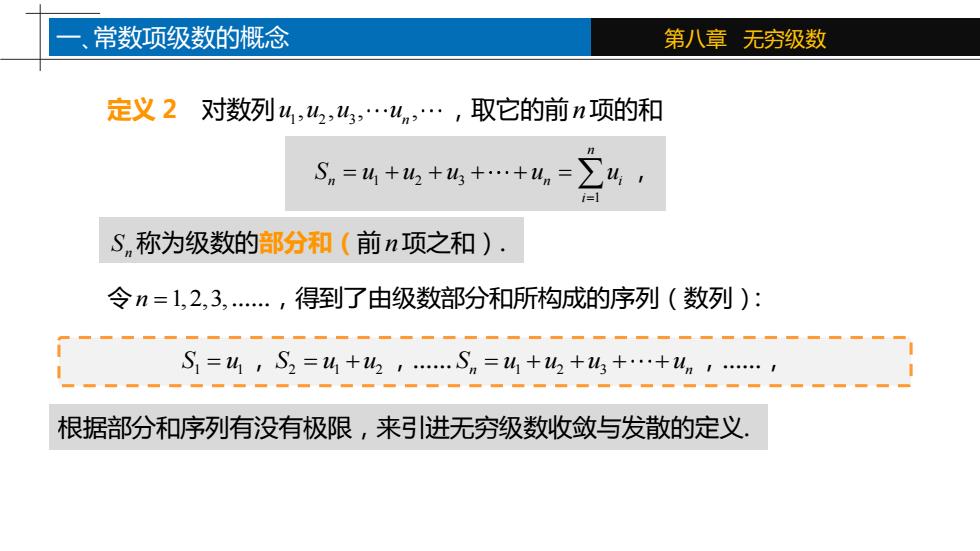
一、常数项级数的概念 第八章无穷级数 定义2对数列4,42,4,.4n,.,取它的前n项的和 Sn=4+山+4++4=∑4, Sn称为级数的部分和(前n项之和). 令n=1,2,3,.,得到了由级数部分和所构成的序列(数列): S1=4,S2=4+42,.Sn=4+h2+43+.+un,. 根据部分和序列有没有极限,来引进无穷级数收敛与发散的定义
第八章 无穷级数 定义 2 对数列 1 2 3 , , , , n u u u u ,取它的前n项的和 1 2 3 1 n n n i i S u u u u u = = + + + + = , n S 称为级数的部分和(前n项之和). 令n =1,2,3,.,得到了由级数部分和所构成的序列(数列): 1 1 S u = , 2 1 2 S u u = + ,. n n 1 2 3 S u u u u = + + + + ,., 根据部分和序列有没有极限,来引进无穷级数收敛与发散的定义. 一、常数项级数的概念

常数项级数的概念 第八章无穷级数 定义3若级数的部分和数列{Sn}有极限S,即1imSn=S,则称无穷级数 11-6 立,收数,这时,极限S就叫做无穷级数父,的和,并写成立=5: 若数列{S,}没有极限,则称无穷级数∑u,发散. n=l 由此可见,讨论无穷级数的收敛问题,实际上就是讨论部分和数列的极限是 否存在
第八章 无穷级数 定义 3 若级数的部分和数列Sn 有极限 S , 即lim n n S S → = ,则称无穷级数 1 n n u = 收敛,这时,极限 S 就叫做无穷级数 1 n n u = 的和,并写成 1 n n u S = = ; 一、常数项级数的概念 由此可见,讨论无穷级数的收敛问题,实际上就是讨论部分和数列的极限是 否存在. 若数列Sn 没有极限,则称无穷级数 1 n n u = 发散