
项的线性化方程式。这种线性化方法称为小偏差线性化方法。 设连续变化的非线性函数为y=了(x),如图2-5所示。取某平衡状态A为工作点,对 应有y。=f(x)。当x=x。+血时,有y=。+。设函数y=fx)在(xo,)点连续 可微,则将它在该点附近用泰勒级数展开为 d2f0四x-2+. y=f(x)=f(xo)+(x-x)+d 当增量(x一x)很小时,略去其高次幂项,则有 -=-a-(9)a-0 令4=y-o=f(x)-fxo),水=x-x,K=(df(x)/d),则线性化方程可简记 为 4y=K4 略去增量符号4,便得到函数在工作点附近的线性化方程为y=K 式中,K=(d山(x)/d)是比例系数,它是函数y=f(x)在A点附近的切线斜率。 少4 图2-5小偏差线性化示意图 [例2-5]铁芯线圈电路如图2-6(a)所示,其磁通Φ与线圈中电流i之间关系如图 26(b)所示。试列写以4,为输入量,1为输出量的电路微分方程。 (a》 图2-6铁芯线圈电路及其特性
13 项的线性化方程式。这种线性化方法称为小偏差线性化方法。 设连续变化的非线性函数为 y = f (x) ,如图 2-5 所示。取某平衡状态 A 为工作点,对 应有 ( ) 0 0 y = f x 。当 x = x + x 0 时,有 y = y + y 0 。设函数 y = f (x) 在 ( , ) 0 0 x y 点连续 可微,则将它在该点附近用泰勒级数展开为 − + − + = = + 2 2 0 2 0 0 ( ) ( ) 2! 1 ( ) ( ) ( ) ( ) 0 0 x x dx d f x x x dx df x y f x f x x x 当增量 ( ) 0 x − x 很小时,略去其高次幂项,则有 ( ) ( ) ( ) ( ) 0 0 0 0 x x dx df x y y f x f x x − − = − = 令 ( ) ( ) 0 0 y = y − y = f x − f x , 0 x = x − x , ( ) 0 ( ) x K = df x dx ,则线性化方程可简记 为 y = Kx 略去增量符号 ,便得到函数在工作点附近的线性化方程为 y = Kx 式中, ( ) 0 ( ) x K = df x dx 是比例系数,它是函数 y = f (x) 在 A 点附近的切线斜率。 图 2-5 小偏差线性化示意图 [例 2-5] 铁芯线圈电路如图 2-6( a )所示,其磁通 与线圈中电流 i 之间关系如图 2-6( b )所示。试列写以 r u 为输入量, i 为输出量的电路微分方程。 图 2-6 铁芯线圈电路及其特性 0 x 0 y A x x y

解设铁芯线圈磁通变化时产生的感应电势为 。=K,p0 al 根据克希霍夫定律可写出电路微分方程为 ”=太@0,质=k,@9由+6 (2-20) 式中的dΦ()/体是线圈中电流i的非线性函数,因此式(2-20)是一个非线性微分方程, 在工程应用中,如果电路的电压和电流只在某平衡点(u,。)附近作微小变化,则可设 u,相对于山,的增量是,i相对于i,的增量是,并设p()在。的附近连续可微,则将 ()在。附近用泰勒级数展开为 ouau))y di 当少足够小时,略去高阶导数项,可得 0-6)=(0)d=kd 式中K=(dD()/d),令AD=D)-D(i),并略去增量符号4,便得到磁通D与线 圈中电流1之间的增量线性化方程为 (i)=Ki (2-21) 由式(2-21)可求得dw0/d=K,代入式(2-20)中,有 K,K+=u (2-22) dt 式(2-22)便是铁芯线圈电路在平衡点(山。,6)的增量线性化方程,若平衡点发生变动,则K 值亦相应改变。 通过上述讨论,应注意以下几点: (1)线性化方程中的参数与选择的工作点有关,工作点不同,相应的参数也不同。因 此,在进行线性化时,应首先确定工作点。 (2)当输入量变化范围较大时,用上述方法进行线性化处理势必引起较大的误差。所 以,要注意它的条件,包括信号变化的范围。 (3)若非线性特性是不连续的,处处不能满足展开成为泰勒级数的条件,这时就不能 进行线性化处理。这类非线性称为本质非线性,对于这类问题,要用非线性自动控制理论来 解决。 2.3传递函数 建立系统数学模型的目的是为了对系统的性能进行分析。在给定外作用及初始条件下, 求解微分方程就可以得到系统的输出响应。这种方法比较直观,特别是借助于电子计算机可
14 解 设铁芯线圈磁通变化时产生的感应电势为 dt d i u K ( ) 1 = 根据克希霍夫定律可写出电路微分方程为 Ri dt di di d i Ri K dt d i ur = K + = + ( ) ( ) 1 1 (2-20) 式中的 d(i) di 是线圈中电流 i 的非线性函数,因此式(2-20)是一个非线性微分方程。 在工程应用中,如果电路的电压和电流只在某平衡点 ( , ) 0 0 u i 附近作微小变化,则可设 r u 相对于 0 u 的增量是 ur ,i 相对于 0 i 的增量是 i ,并设 (i) 在 0 i 的附近连续可微,则将 (i) 在 0 i 附近用泰勒级数展开为 + + = + 2 2 2 0 ( ) ( ) 2! ( ) 1 ( ) ( ) 0 0 i di d i i di d i i i i i 当 i 足够小时,略去高阶导数项,可得 i K i di d i i i i = − = 0 ( ) ( ) ( ) 0 式中 0 ( ( ) ) di i K = d i ,令 ( ) ( ) 0 = i − i ,并略去增量符号 ,便得到磁通 与线 圈中电流 i 之间的增量线性化方程为 (i) = Ki (2-21) 由式(2-21)可求得 d(i) di = K ,代入式(2-20)中,有 Ri ur dt di K1K + = (2-22) 式(2-22)便是铁芯线圈电路在平衡点 ( , ) 0 0 u i 的增量线性化方程,若平衡点发生变动,则 K 值亦相应改变。 通过上述讨论,应注意以下几点: (1)线性化方程中的参数与选择的工作点有关,工作点不同,相应的参数也不同。因 此,在进行线性化时,应首先确定工作点。 (2)当输入量变化范围较大时,用上述方法进行线性化处理势必引起较大的误差。所 以,要注意它的条件,包括信号变化的范围。 (3)若非线性特性是不连续的,处处不能满足展开成为泰勒级数的条件,这时就不能 进行线性化处理。这类非线性称为本质非线性,对于这类问题,要用非线性自动控制理论来 解决。 2.3 传递函数 建立系统数学模型的目的是为了对系统的性能进行分析。在给定外作用及初始条件下, 求解微分方程就可以得到系统的输出响应。这种方法比较直观,特别是借助于电子计算机可

以迅速而准确地求得结果。但是如果系统的结构改变或某个参数变化时,就要重新列写并求 解微分方程,不便于对系统的分析和设计。 拉氏变换是 求解线性微分方程的简捷方法。当采用这一方法时,微分方程的求解问题化 为代数方程和查表求解的问题,这样就使计算大为简使。更重要的是,由于采用了这一方法 能把以线性微分方程式描述系统的动态性能的数学模型,转换为在复数域的代数形式的数学 模型一一传递函数。传递函数不仅可以表征系统的动态性能,而且可以用来研究系统的结构 或参数变化对系统性能的影响。经典控制理论中广泛应用的频率法和根轨迹法,就是以传递 函数为基础建立起来的,传递函数是经典控制理论中最基本和最重要的概念 2.3.1传递函数的定义和性质 1.定义线性定常系统的传递函数,定义为零初始条件下,系统输出量的拉氏变换与 输入量的拉氏变换之比。 设线性定常系统由下述阶线性常微分方程描述: 00+ahm0+.+a-d0+a,0 (2-23) d d =bo diu()+b =40++b-d0+b.0 式中y是系统的输出量,)是系统的输入量,a,=L,2,.,m)和 b,U=1,2,m)是与系统结构和参数有关的常系数。设)和y)及各阶导数在 【=0时的值均为零,即零初始条件,则对上式中各项分别求拉氏变换,并令 Y(s)=t,U(s)=u(t,可得s的代数方程为 [aos"+as"+.+as+a lY(s)=[bos"+bs"-+.+bs+b (s) (2-24) 于是,由定义得系统传递函数为 Y(s)bosm+bsm+.+bms+b )-U(S)d. (2-25) 2.性质传递函数具有以下性质: (1)传递函数是复变量s的有理真分式函数,具有复变函数的所有性质。m≤n且所 有系数均为实数。 (2)传递函数是系统或元件数学模型的另一种形式,是一种用系统参数表示输出量与 输入量之间关系的表达式。它只取决于系统或元件的结构和参数,而与输入量的形式无关, 也不反映系统内部的任何信总。 (3)传递函数与微分方程有相通性。只要把系统或元件微分方程中各阶导数用相应阶 次的变量s代替,就很容易求得系统或元件的传递函数。 (4)传递函数G(s)的拉氏反变换是脉冲响应g()。 g)是系统在单位脉冲()输入时的输出响应。此时U(s)=④8)=1,故有 g()=-'[Y(s】=-[GsU(s】=-'[G(s】. 15
15 以迅速而准确地求得结果。但是如果系统的结构改变或某个参数变化时,就要重新列写并求 解微分方程,不便于对系统的分析和设计。 拉氏变换是求解线性微分方程的简捷方法。当采用这一方法时,微分方程的求解问题化 为代数方程和查表求解的问题,这样就使计算大为简便。更重要的是,由于采用了这一方法, 能把以线性微分方程式描述系统的动态性能的数学模型,转换为在复数域的代数形式的数学 模型——传递函数。传递函数不仅可以表征系统的动态性能,而且可以用来研究系统的结构 或参数变化对系统性能的影响。经典控制理论中广泛应用的频率法和根轨迹法,就是以传递 函数为基础建立起来的,传递函数是经典控制理论中最基本和最重要的概念。 2.3.1 传递函数的定义和性质 1.定义 线性定常系统的传递函数,定义为零初始条件下,系统输出量的拉氏变换与 输入量的拉氏变换之比。 设线性定常系统由下述 n 阶线性常微分方程描述: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 0 1 1 1 1 0 1 u t b u t dt d u t b dt d u t b dt d b y t a y t dt d y t a dt d y t a dt d a m m m m m m n n n n n n = + + + + + + + + − − − − − − (2-23) 式 中 y(t) 是系统的输出量, u(t) 是系统的输入量 , a (i 1, 2, , n) i = 和 b ( j 1, 2, , m) j = 是与系统结构和参数有关的常系数。设 u(t) 和 y(t) 及各阶导数在 t = 0 时 的 值 均 为 零, 即 零 初始 条 件 ,则 对 上 式中 各 项 分别 求 拉 氏变 换 , 并 令 Y(s) = [y(t)], U(s) = [u(t)] ,可得 s 的代数方程为 [ ] ( ) [ ] ( ) 1 1 1 0 1 1 0 1 a s a s a s a Y s b s b s b s b U s m m m m n n n n + + + + = + + + − + − − − (2-24) 于是,由定义得系统传递函数为 n n n n m m m m a s a s a s a b s b s b s b U S Y s G s + + + + + + + + = = − − − − 1 1 0 1 1 1 0 1 ( ) ( ) ( ) (2-25) 2.性质 传递函数具有以下性质: (1)传递函数是复变量 s 的有理真分式函数,具有复变函数的所有性质。 m n 且所 有系数均为实数。 (2)传递函数是系统或元件数学模型的另一种形式,是一种用系统参数表示输出量与 输入量之间关系的表达式。它只取决于系统或元件的结构和参数,而与输入量的形式无关, 也不反映系统内部的任何信息。 (3)传递函数与微分方程有相通性。只要把系统或元件微分方程中各阶导数用相应阶 次的变量 s 代替,就很容易求得系统或元件的传递函数。 (4)传递函数 G(s) 的拉氏反变换是脉冲响应 g(t)。 g(t) 是 系 统 在 单 位 脉冲 (t) 输入时的输出响应。此时 U(s) = [ (t)] = 1 ,故有 ( ) [ ( )] [ ( ) ( )] [ ( )] 1 1 1 g t Y s G s U s G s − − − = = =

对于简单的系统或元件,首先列出它的输出量与输入量的微分方程,求其在零初始条 件下的拉氏变换,然后由输出量与输入量的拉氏变换之比,即可求得系统的传递函数。对于 较复杂的系统或元件,可以先将其分解成各局部环节,求得环节的传递函数,然后利用本 所介绍的结构图变换法则,计算系统总的传速函数。 下面举例说明求取简单环节的传递函数的步骤。 [例26]图2-1所示RLC网络的微分方程为 1cdu@+Rc恤@+u.0=u,0 at- at 当初始条件为零时,拉氏变换为 (LCs2+RCs+1)U.(s)=U.(s) 则传递函数为 a0-器7c西 2.3.2典型环节的传递函数 一个物理系统是有许多元件组合而成的。虽然各种元件的具体结构和作用原理是多种多 样的,但若抛开其具体结构和物理特点,研究其运动规律和数学模型的共性,就可以划分成 为数不多的几种典型环节。这些典型环节是:比例环节、微分环节、积分环节、比例微分环 节、一阶惯性环节、二阶振荡环节和延迟环节。应该指出,由于典型环节是按数学模型的共 性划分的,它和具体元件不一定是 一对应的。换句话说,典型环节只代表一种特定的运动 规律, 不一定是一种具体的元件。 1比例环节 比例环节又称放大环节,其输出量与输入量之间的关系为一种固定的比例关系。这就是 说,它的输出量能够无失真、无迟后地按一定的比例复现输入量。比例环节的表达式为 (2-26) 比例环节的传递函数为 G(S)=Y(s)=K (2-27) 0(S) 在物理系统中无弹性变形的杠杆、非线性和时间常数可以忽略不计的电子放大器、传动 链之速比以及测速发电机的电压和转速的关系 都可以认为是比例环节。但是也应指出, 全理想的比例环节在实际上是不存在的。杠杆和传动链中总存在弹性变形,输入信号的频率 改变时电子放大器的放大系数也会发生变化,测速发电机电压与转速之间的关系也不完全是 线性关系。因此把上述这些环节当作比例环节是一种理想化的方法。在很多情况下这样做既 不影响问圆的性质,又能使分析过程简化。但一定要注意理想化的条件和适用范围,以免导 致错误的结论 微分环节 微分环节是自动控制系统中经常应用的环节。 (1)理想微分环节 理想微分环节的特点是在暂态过程中,输出量为输入量的微分,即
16 对于简单的系统或元件,首先列出它的输出量与输入量的微分方程,求其在零初始条 件下的拉氏变换,然后由输出量与输入量的拉氏变换之比,即可求得系统的传递函数。对于 较复杂的系统或元件,可以先将其分解成各局部环节,求得环节的传递函数,然后利用本章 所介绍的结构图变换法则,计算系统总的传递函数。 下面举例说明求取简单环节的传递函数的步骤。 [例 2-6] 图 2-1 所示 RLC 网络的微分方程为 ( ) ( ) ( ) ( ) 2 2 u t u t dt du t RC dt d u t LC c r c c + + = 当初始条件为零时,拉氏变换为 ( 1) ( ) ( ) 2 LCs RCs U s U s + + c = r 则传递函数为 1 1 ( ) ( ) ( ) 2 + + = = U s LCs RCs U s G s r c 2.3.2 典型环节的传递函数 一个物理系统是有许多元件组合而成的。虽然各种元件的具体结构和作用原理是多种多 样的,但若抛开其具体结构和物理特点,研究其运动规律和数学模型的共性,就可以划分成 为数不多的几种典型环节。这些典型环节是:比例环节、微分环节、积分环节、比例微分环 节、一阶惯性环节、二阶振荡环节和延迟环节。应该指出,由于典型环节是按数学模型的共 性划分的,它和具体元件不一定是一一对应的。换句话说,典型环节只代表一种特定的运动 规律,不一定是一种具体的元件。 1 比例环节 比例环节又称放大环节,其输出量与输入量之间的关系为一种固定的比例关系。这就是 说,它的输出量能够无失真、无迟后地按一定的比例复现输入量。比例环节的表达式为 y(t) = Ku(t) (2-26) 比例环节的传递函数为 K U S Y s G s = = ( ) ( ) ( ) (2-27) 在物理系统中无弹性变形的杠杆、非线性和时间常数可以忽略不计的电子放大器、传动 链之速比以及测速发电机的电压和转速的关系,都可以认为是比例环节。但是也应指出,完 全理想的比例环节在实际上是不存在的。杠杆和传动链中总存在弹性变形,输入信号的频率 改变时电子放大器的放大系数也会发生变化,测速发电机电压与转速之间的关系也不完全是 线性关系。因此把上述这些环节当作比例环节是一种理想化的方法。在很多情况下这样做既 不影响问题的性质,又能使分析过程简化。但一定要注意理想化的条件和适用范围,以免导 致错误的结论。 2 微分环节 微分环节是自动控制系统中经常应用的环节。 (1)理想微分环节 理想微分环节的特点是在暂态过程中,输出量为输入量的微分,即
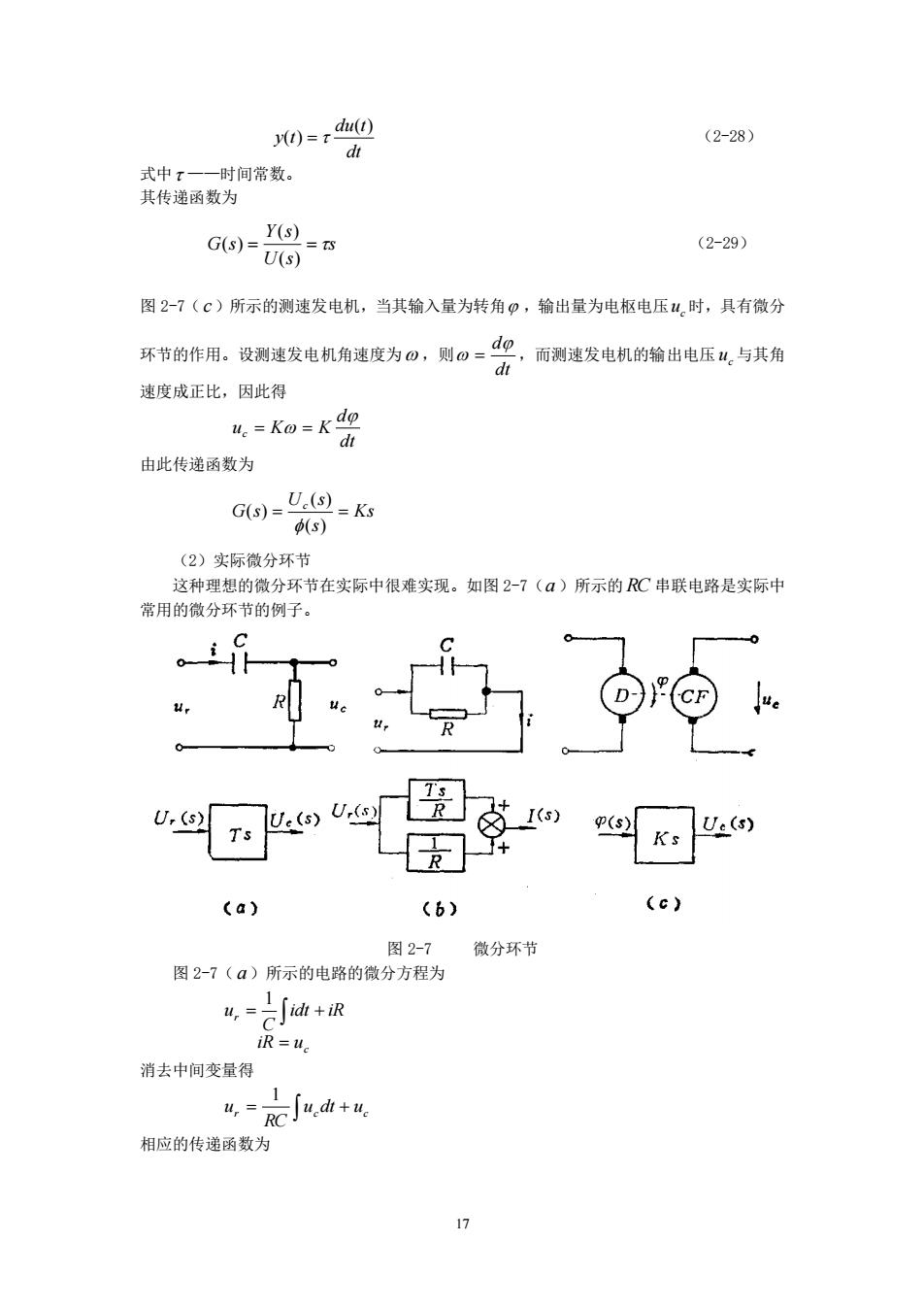
0=9 (2-28) 一时间常数 co得 (2-29) 图2-7(c)所示的测速发电机,当其输入量为转角p,输出量为电枢电压时,具有微分 环节的作用。设测速发电机角速度为0,则。-华,而测速发电机的输出电压,与其角 速度成正比,因此得 由此传递函数为 G=,=k后 () (2)实际微分环节 这种理想的微分环节在实际中很难实现。如图2-7(a)所示的RC串联电路是实际中 常用的微分环节的例子。 9:匹9a是这,@K U:(s) LR]+ (a) (6) (c) 图2-7 微分环节 图2-7(a)所示的电路的微分方程为 4,=d+R iR=ue 消去中间变量得 相应的传递函数为 1
17 dt du t y t ( ) ( ) = (2-28) 式中 ——时间常数。 其传递函数为 s U s Y s G s = = ( ) ( ) ( ) (2-29) 图 2-7( c )所示的测速发电机,当其输入量为转角 ,输出量为电枢电压 c u 时,具有微分 环节的作用。设测速发电机角速度为 ,则 dt d = ,而测速发电机的输出电压 c u 与其角 速度成正比,因此得 dt d uc K K = = 由此传递函数为 Ks s U s G s c = = ( ) ( ) ( ) (2)实际微分环节 这种理想的微分环节在实际中很难实现。如图 2-7( a )所示的 RC 串联电路是实际中 常用的微分环节的例子。 图 2-7 微分环节 图 2-7( a )所示的电路的微分方程为 c r iR u idt iR C u = = + 1 消去中间变量得 r = ucdt + uc RC u 1 相应的传递函数为