
说明 16 口S=∫np(x)dx=1 p(x) x x2 X 51=P(x1<X<x2)=fip(x)dx
说明 ∞− = �� ∞ 𝒑 𝒙 𝒅𝒙 = 𝟏 �𝒙� = �𝒙� ≥ �� > �𝒙� �� = �𝑺� 𝒙𝟐 𝒑 𝒙 𝒅𝒙 16 1 S1 1 x • 2 x • 0 x p(x)

连续型v.F(x),p(x)性质 17 (3)连续型.v.X在任一点a取值的概率等于0,即 P(X=a)=0. 证:0≤P(X=a)≤P(a-Ax<X≤a)=2axp(odx lim p(x)dx=0,.P(X=a)=0 △X→0 a-△x P{a≤X≤bFP{a<X≤b}=P{a≤X<b} =P{a<X<b}. 连续型随机变量的概率与区间的开闭无关
连续型r.v. 𝑭 𝒙 , 𝒑(𝒙)性质 (3)连续型r.v. 𝑿在任一点𝒂取值的概率等于0,即 𝑷 𝑿 = 𝒂 = 𝟎. �𝚫�−�� = �� ≥ �� > �𝚫� − �� �� ≥ �� = �� �� ≥ ��:证 𝒂 𝒑 𝒙 𝒅𝒙 ∵ lim 𝚫𝒙→𝟎 න 𝒂−𝚫𝒙 𝒂 𝒑 𝒙 𝒅𝒙 = 𝟎, ∴ 𝑷 𝑿 = 𝒂 = 𝟎 17

连续型v.F(x),p(x)性质 18 口(4)若p(x)在点x处连续,则有 F'(x)=p(x). 证:p(x)连续,则F(x)可导. P国=&广,pna=n0
连续型r.v. 𝑭 𝒙 , 𝒑(𝒙)性质 (4) 若𝒑(𝒙)在点𝒙处连续,则有 𝑭 ′ 𝒙 = 𝒑 𝒙 . 证:𝒑 𝒙 连续,则𝑭(𝒙)可导. 𝑭 ′ 𝒙 = 𝒅 𝒅𝒙 න −∞ 𝒙 𝒑 𝒙 𝒅𝒙 = 𝒑 𝒙 . 18

例 19 设随机变量X具有概率密度 kx, 0≤x<3, 比 (x)=X2-),3st≤4, 0, 其它 (I)确定常数k; (2)求X的分布函数 (B)求PI<Xs 解:(由np(x)dx=l, 得」 kxdx+-ar=l,解之得 k=6
例 19 ( ) { }. ( ) ; ( ) ; , . , , , , ( ) 2 7 3 1 1 2 0 3 4 2 2 0 3 − = P X k X x x kx x p x X 求 确定常数 求 的分布函数 其 它 设随机变量 具有概率密度
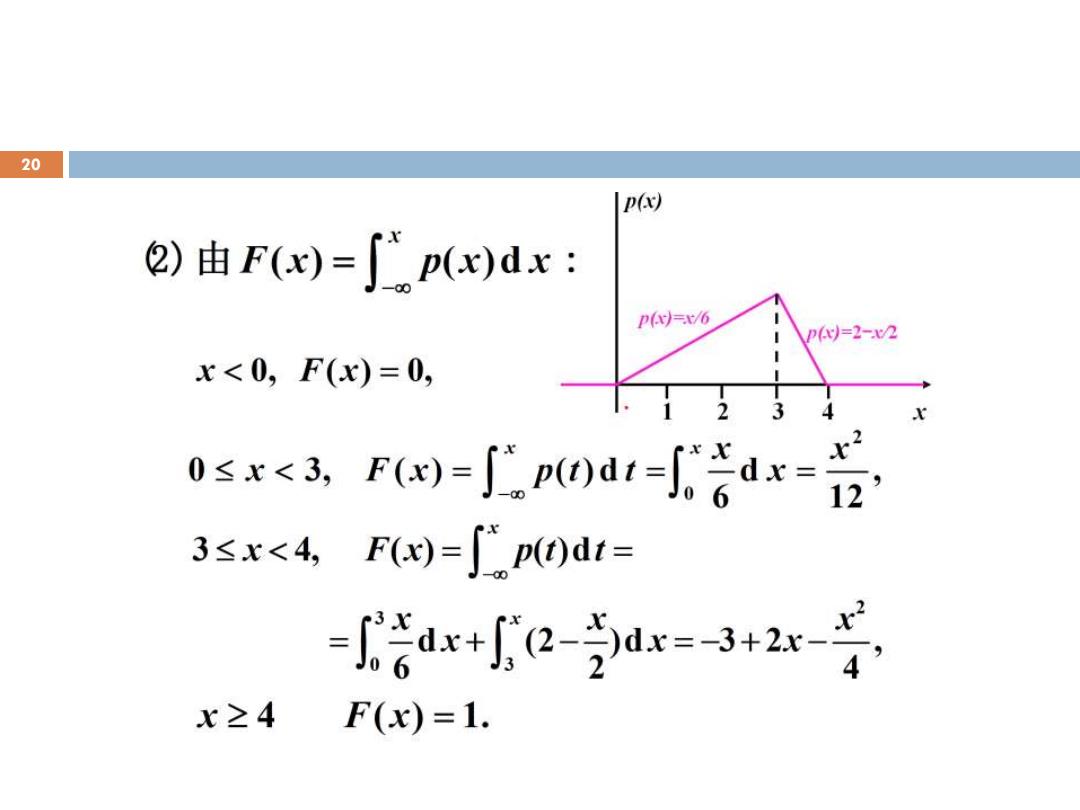
20 p 2)由F(x)=∫p(x)dx: P=x/6 p)=2-e2 x<0,F(x)=0, 234 x 05c四=0-g4= 3≤x<4,F)=p0dt= -a+0-a=3+2号 4 x≥4 F(x)=1
20