
水人 2.1矩阵的概念 尚本 主题调 1.矩阵 2.同型矩阵 3.上(下)三角矩阵 4.对角矩阵 5,单位矩阵 6.数量矩阵 返回 河套大学《线性代数》课件 第二章矩阵 快东学可
快乐学习 以人 2.1 矩阵的概念 为本 主 题 词 1.矩阵 2.同型矩阵 3.上(下)三角矩阵 4.对角矩阵 5.单位矩阵 6.数量矩阵 1 河套大学《线性代数》课件 第二章 矩阵 返回

水人 2.1.1引例 尚本 本节中的几个例子展示了如何将某个数学问题 或实际问题与一张数表一一 矩阵联系起来,这实 际上是对一个数学问题或实际问题进行数学建模 的第一步 例2.1.1线性方程组 aX±Q2X2++anX,b 021X±022X2+…±02nXn=b2 0年00用 anmx±anmX2+…+AX三bn 河套大学《线性代数》课件 第二章矩阵 快东学司
快乐学习 以人 2.1.1 引例 为本 本节中的几个例子展示了如何将某个数学问题 或实际问题与一张数表——矩阵联系起来,这实 际上是对一个数学问题或实际问题进行数学建模 的第一步. 例2.1.1 线性方程组 + + + = + + + = + + + = . , , 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 a x a x a x b a x a x a x b a x a x a x b n n n n n n n n n n 河套大学《线性代数》课件 第二章 矩阵

水人 2.1.1引例(续10 尚本 的系数a位,青/=1,2,,n)与常数项b,01,2,,n 按原位置构成一数表: a d12 b 02 A2n b An2 b 根据克拉默法则,该数表决定着上述方程组 是否有解以及如果有解,解是什么?解的结构如 何等,因此研究这个表很有意义, 河套大学《线性代数》课件 第二章矩阵 快东骨司
快乐学习 以人 为本 . 2 1 2 1 2 22 12 1 21 11 nn n n n n n b b b a a a a a a a a a 2.1.1 引例(续1) 根据克拉默法则,该数表决定着上述方程组 是否有解以及如果有解,解是什么?解的结构如 何等,因此研究这个表很有意义. 河套大学《线性代数》课件 第二章 矩阵 a (i , j 1, 2 , , n) ij = b ( j 1, 2 , , n) j = 按原位置构成一数表: 的系数 与常数项
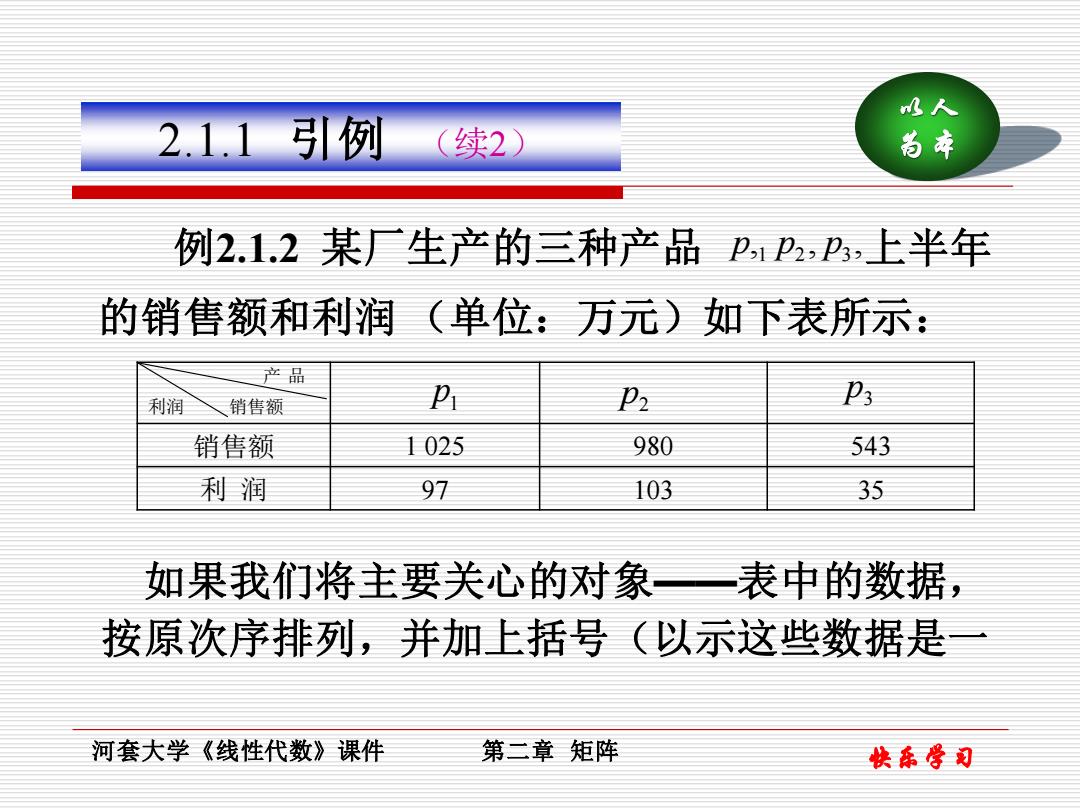
水人 2.1.1引例 (续2) 尚本 例2.1.2某厂生产的三种产品p1P2,卫,上半年 的销售额和利润(单位:万元)如下表所示: 产品 利润 销售额 P 卫3 销售额 1025 980 543 利润 97 103 35 如果我们将主要关心的对象一表中的数据, 按原次序排列,并加上括号(以示这些数据是 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.1.1 引例 (续2) 为本 , , , 例2.1.2 某厂生产的三种产品 p 1 p2 p3 上半年 的销售额和利润 (单位:万元)如下表所示: 销售额 1 025 980 543 利 润 97 103 35 利润 销售额 产 品 1 p 2 p 3 p 如果我们将主要关心的对象——表中的数据, 按原次序排列,并加上括号(以示这些数据是一 河套大学《线性代数》课件 第二章 矩阵

水人 2.1.1引例■(续3) 尚本 个不可分割的整体),那么,就可以简略地表 示为矩形数表: 1025 890 543 97 103 35 例2.1.3假设要将民用煤从3个产地运往4个销 售地,若用a,表示由产地卫,(i=1,2,3)运到销售地 S0=1,2,3,4的数量(单位:),则调运方案 河套大学《线性代数》课件 第二章矩阵 快乐骨司
快乐学习 以人 2.1.1 引例 (续3) 为本 个不可分割的整体),那么,就可以 简略地 表 示为矩形数表: . 35 543 103 890 97 1025 例2.1.3 假设要将民用煤从3个产地运往4个销 售地,若用 aij 表示由产地 i p (i = 1,2,3) 运到销售地 j s ( j = 1,2,3,4) 的数量(单位:t),则调运方案 河套大学《线性代数》课件 第二章 矩阵