举例:角分布中的前后不对称 T 后向 前向 例如:e++e→J/w→e+e -1 0 B:后向计数;F:前向计数;N=B+F 若上述过程平均事例数为V,则观测到N个事例的 概率服从泊松分布 N! 在这N个事例中,如果单个事例为前向的概率为f, N! 则观测到F个前向事例的概率满足二项式分布 f(-A)" BL FL 观测到上述过程N个事例且有F个为前向事例的概率为 P=PP=e"()xe-v(1- 是前向与后向两 个独立泊松分布 F BL 的产物!
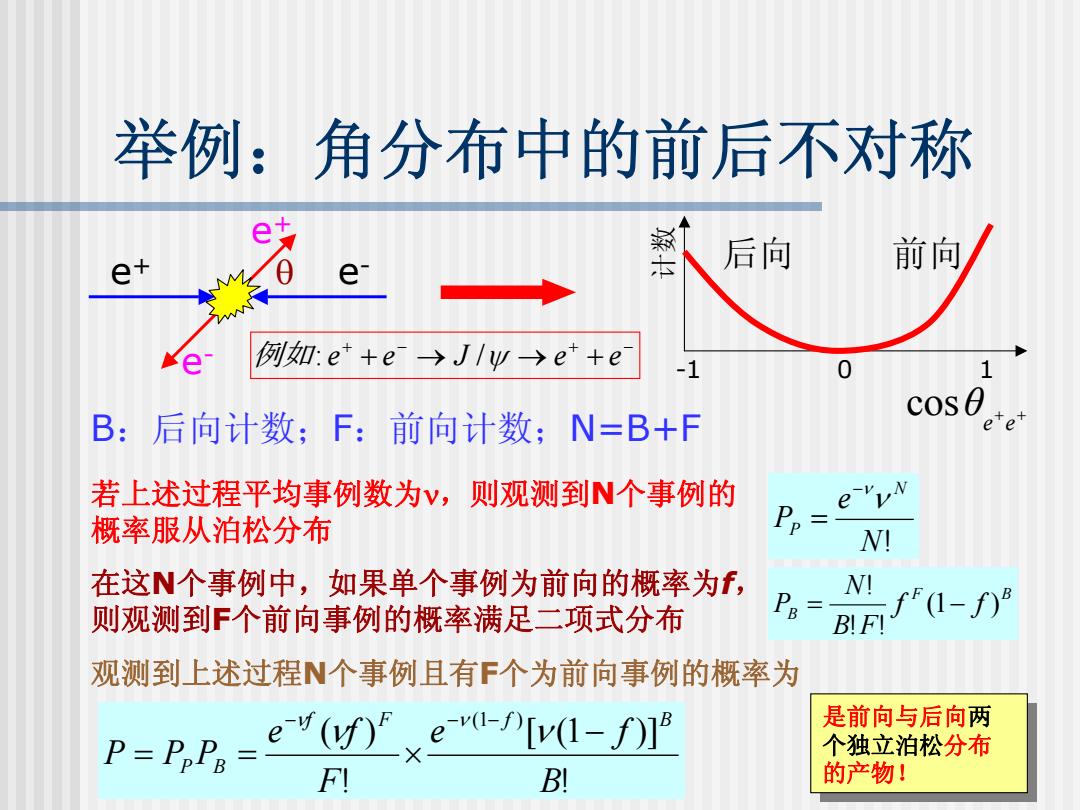
举例:角分布中的前后不对称 e + e - e + e - θ -1 0 1 计数 + + e e cos θ 后向 前向 B:后向计数; F:前向计数;N=B+F + − + − 例如: e + e → J /ψ → e + e 若上述过程平均事例数为 ν,则观测到 N个事例的 概率服从泊松分布 N! e P N P ν −ν = 在这 N个事例中,如果单个事例为前向的概率为 f, 则观测到 F个前向事例的概率满足二项式分布 F B B f f B F N P ( 1 ) ! ! ! = − 观测到上述过程 N个事例且有 F个为前向事例的概率为 ! [ ( 1 )] ! ( ) (1 ) B e f F e f P P P f F f B P B − = = × − − − ν ν ν ν 是前向与后向两 个独立泊松分布 的产物! 是前向与后向 两 个独立泊松分布 的产物!

直方图中的误差处理 总数N 在前述角分布前后不对称的 各区间频数n1,n2,n3 析,如果将角分布的前后向再 分几个部分,所得到的结论具 每个格子的 有普遍性。即所观测分布的直 误差为Wn, 方图可看成与 1.一个事例总数满足泊松分布和 在每个区间得到n1,n2,n3..事例 数为多项式分布有关: 2. 或者是直方图中每个区间互相 独立的泊松分布有关。 N=√W 或 观测量 (△N)2=N=(△n,)2+(△n2)2+(△n3)2+. =n1+n2+n3+=N
直方图中的误差处理 观测量 频数在前述角分布前后不对称的 析,如果将角分布的前后向再 分几个部分,所得到的结论具 有普遍性。即所观测分布的直 方图可看成与 1. 一个事例总数满足泊松分布和 在每个区间得到 n 1,n 2,n 3 …事例 数为多项式分布有关; 2. 或者是直方图中每个区间互相 独立的泊松分布有关。 总数 N 各区间频数 n 1,n 2,n 3 … n n n N N N n n n N N = + + + = Δ = = Δ + Δ + Δ + Δ = ... ( ) ( ) ( ) ( ) ... 或 1 2 3 2 3 2 2 2 1 2 每个格子的 误差为 i n