
定义2.f(x)在区间I上的原函数全体称为f(x)在1 上的不定积分,记作f(x)dx,其中 ∫- 积分号; ∫(x)一被积函数; 积分变量; f(x)dx一被积表达式 若F'(x)=f(x),则 「f(x)drx=F(x)+C(C为任意常数) 例如, [e*dx ex+C C称为积分常数 ∫x2dx=}x3+C 不可丢! sin xdx cos x+C HIGH EDUCATION PRESS 机动目录上页下页返回结束
定义 2. 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号; — 被积函数; — 积分变量; — 被积表达式. 若 则 ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如, = e x x d e C x + = x dx 2 x + C 3 3 1 = sin xdx − cos x + C 记作 机动 目录 上页 下页 返回 结束
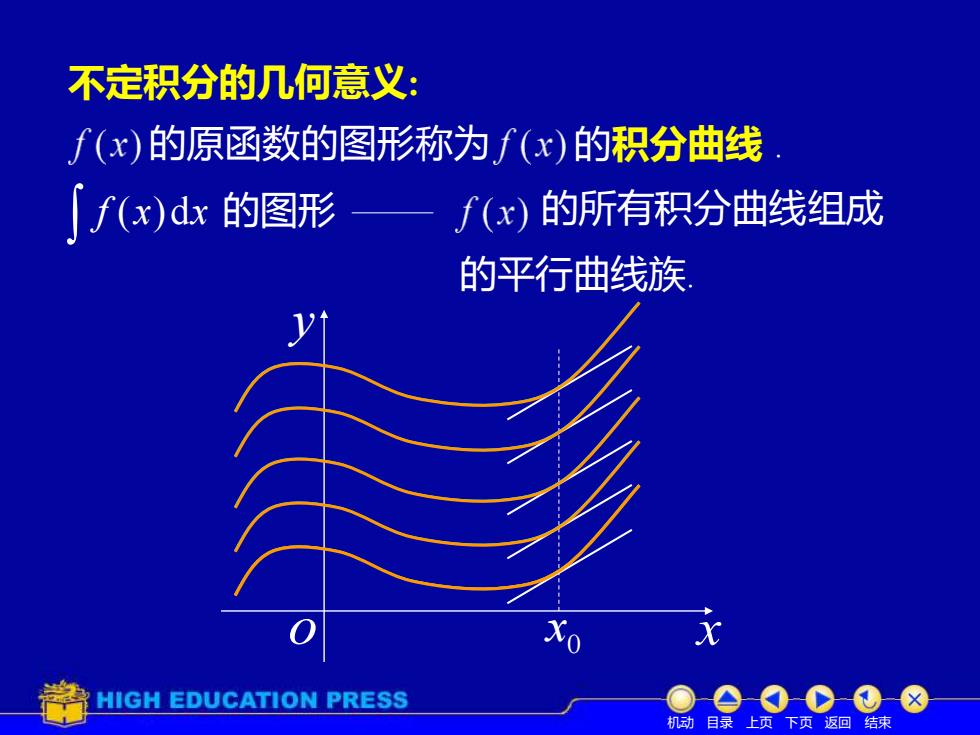
不定积分的几何意义: f(x)的原函数的图形称为f(x)的积分曲线 ∫fx)dk的图形 —f(x)的所有积分曲线组成 的平行曲线族 HIGH EDUCATION PRESS 动目录上页下页返回结束
不定积分的几何意义: 的原函数的图形称为 f (x)dx 的图形 的所有积分曲线组成 的平行曲线族. y o x0 x 机动 目录 上页 下页 返回 结束 的积分曲线

例1.设曲线通过点(1,2),且其上任一点处的切线 斜率等于该点横坐标的两倍,求此曲线的方程 解: ,y'=2x .y=∫2xdx=x2+C 所求曲线过点(1,2),故有 2=12+C C=1 因此所求曲线为y=x2+1 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例1. 设曲线通过点( 1 , 2 ) , 且其上任一点处的切线 斜率等于该点横坐标的两倍, 求此曲线的方程. 解: 所求曲线过点 ( 1 , 2 ) , 故有 因此所求曲线为 1 2 y = x + 机动 目录 上页 下页 返回 结束 y o x (1, 2)