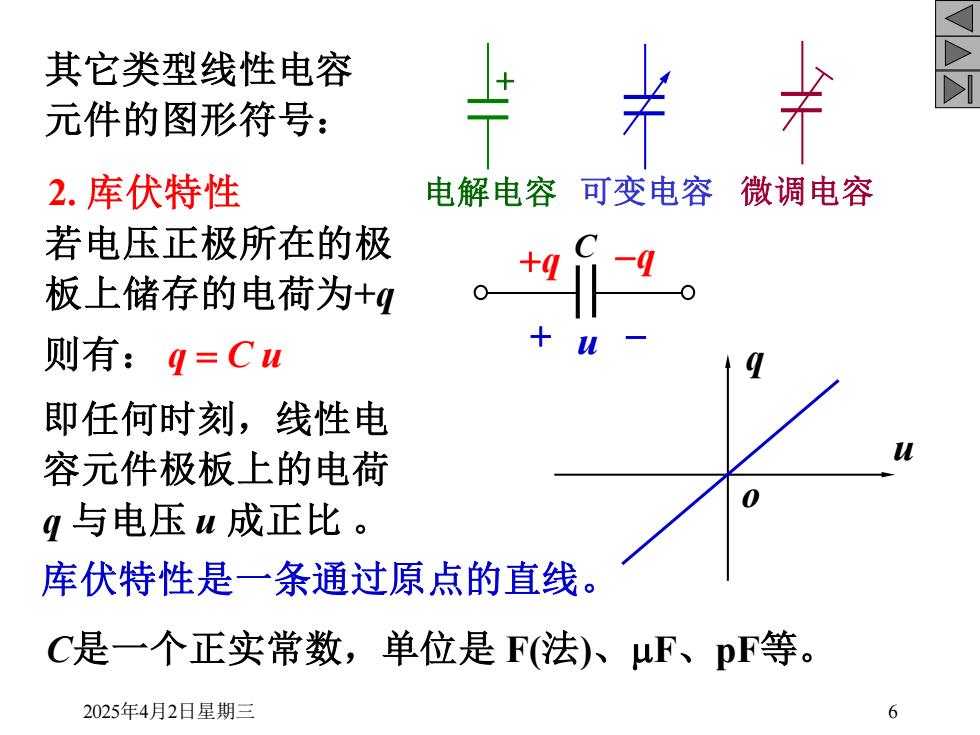
其它类型线性电容 元件的图形符号: 兰卡关 2.库伏特性 电解电容可变电容微调电容 若电压正极所在的极 板上储存的电荷为+4 则有:q=Cu 即任何时刻,线性电 容元件极板上的电荷 q与电压u成正比 。 库伏特性是一条通过原点的直线 C是一个正实常数,单位是F(法)、uF、pF等。 2025年4月2日星期三 6
2025年4月2日星期三 6 其它类型线性电容 元件的图形符号: 2. 库伏特性 C是一个正实常数,单位是 F(法)、mF、pF等。 则有: q = C u o u q + 电解电容 可变电容 微调电容 库伏特性是一条通过原点的直线。 + u - +q -q 若电压正极所在的极 C 板上储存的电荷为+q 即任何时刻,线性电 容元件极板上的电荷 q 与电压 u 成正比

3.伏安关系 若C的i、u取关联参考方向,则有: i= dq d(Cu) 当C为常数时有: dt dt i=C du dt 该式表明: (1)i的大小取决于u的变化率,与W的大小无关! 电容是动态元件; (2)当w为常数(直流)时,i=0。电容相当于开路, 电容有“隔直通交”的作用; (3)实际电路中通过电容的电流为有限值, 则电容电压山不能跃变,必是时间的连续函数。 2025年4月2日星期三
2025年4月2日星期三 7 3. 伏安关系 电容有“隔直通交”的作用; i = dq dt = d(Cu) dt i = du dt C 当C为常数时有: + u - i C q = Cu 若C的i、u取关联参考方向,则有: (1) i 的大小取决于 u 的变化率,与 u 的大小无关! (3) 实际电路中通过电容的电流 i为有限值, 电容是动态元件; (2) 当 u 为常数(直流)时,i = 0。电容相当于开路, 则电容电压 u 不能跃变,必是时间的连续函数。 该式表明:

伏安关系的积分形式 由i=空得g0i0d-∫gd5+9a5听 以为计时起点。 0=g)+(d5 将g=Cu代入得u0=W+亡(⑤d5 表明 电容元件有记忆电流的作用,故称电容为记忆元件。 还需要指出两点:()当山,为非关联方向时,上 述微分和积分表达式前要冠以负号; (2)上式中()称为电容电压的初始值,它反映电 容初始时刻的储能状况,也称为初始状态。 2025年4月2日星期三 8
2025年4月2日星期三 8 伏安关系的积分形式 q(t) = ∫ t -∞ i(x) dx = t0 -∞ i(x) dx +∫ t t0 i(x) dx 以t0为计时起点 q(t) = q(t0 ) + ∫ t t0 i(x) dx 将q = C u 代入得 i = dq dt 由 得 u(t) = u(t0 ) + ∫ t t0 i(x) dx C 1 电容元件有记忆电流的作用,故称电容为记忆元件。 还需要指出两点:(1)当 u,i为非关联方向时,上 述微分和积分表达式前要冠以负号 ; (2)上式中u(t0 )称为电容电压的初始值,它反映电 容初始时刻的储能状况,也称为初始状态。 表明

3.功率/电场能量 u和采用关联参考方向时p=ui=CM du dt t从-∞到任意时刻t吸收的电场能量: u(t u() mfcu6ak=c9au9=ori⑤ u(-∞) w=7c0-7cu(-∞) 若在t=一oo时,电容处于未充电状态:(-oo)=0, 其电场能量也为0。则电容元件在任何时刻所储存 的电场能量将等于它所吸收的能量: w() Cu2(t) 2025年4月2日星期三 9
2025年4月2日星期三 9 3. 功率/电场能量 p = ui = Cu du dt t从-∞到任意时刻 t 吸收的电场能量: wc = ∫ -∞ t C u(x) du(x) dt dt = C u(-∞) u(t) u(x)du(x) = 2 1 Cu2 (x) u(t) u(-∞) u和i采用关联参考方向时 wc = 2 1 Cu2 (t) - 2 1 Cu2 (-∞) 若在t =-∞时,电容处于未充电状态: u(-∞)=0, 其电场能量也为0。 的电场能量将等于它所吸收的能量: wc (t) = 2 1 Cu2 (t) 则电容元件在任何时刻所储存

从t~时间,电容元件吸收的能量为 wc)-子c6)=W)-W. 等于元件在2和t时刻的电场能量之差。 充电时,u(t2)川>u(1)川, 释放的能量≤吸收的能 W(2)>W(G),电容元 量,是无源元件。 件吸收能量; 如果电容元件的库伏 放电时,lu(2)1<l(t1)川, 特性不是通过原点的 W(2)<W(),电容元 直线,则称为非线性 件把存储的电场能量释 电容元件。 放出来。 例如变容二极管,其 电容是一种储能元件, 容量随电压而变。 不消耗电能。 2025年4月2日星期三 10
2025年4月2日星期三 10 等于元件在t2和t1时刻的电场能量之差。 Wc = 2 1 Cu2 (t2 ) - 2 1 Cu2 (t1 ) = Wc (t2 )-Wc (t1 ) 从t1 ~t2时间,电容元件吸收的能量为 充电时,|u(t2 )|>|u(t1 )|, Wc (t2 )>Wc (t1 ),电容元 件吸收能量; 放电时,|u(t2 )|<|u(t1 )|, Wc (t2 )<Wc (t1 ),电容元 件把存储的电场能量释 放出来。 电容是一种储能元件, 不消耗电能。 释放的能量≤吸收的能 量,是无源元件。 如果电容元件的库伏 特性不是通过原点的 直线,则称为非线性 电容元件。 例如变容二极管,其 容量随电压而变