
RLC电路的零输入响应 RLC电路的零输入响应,即uc(O)=O时电路的响应。 ducRC dt dt2 pr duc +uc =0 diue R duc ,1 dt2 4c=0 L dt 由微分方程理论可知,齐次方程解答的形式由特征方 程根的性质决定。特征方程为 s2+ R 1 S+ L R S1,2 11
RLC电路的零输入响应 ❖ RLC电路的零输入响应,即uoc(0)=0时电路的响应。 11 0 1 0 2 2 2 2 + + = + + = C C C C C C u dt LC du L R dt d u u dt du RC dt d u LC ❖ 由微分方程理论可知,齐次方程解答的形式由特征方 程根的性质决定。特征方程为 L LC R L R s LC s L R s 1 2 2 0 1 2 1,2 2 − = − + + =

特征根性质 特征根称为电路的固有频率,它将确定零输入响应的 形式。由于R、L、C数值不同,固有频率s和s2可出现 三种不同的情况: R 2L LC S和S2为不相等的负实数; 2) R S和S2为相等的负实数; 2L 3) 1 S和S2为共轭复数,实部为负; S1,2 12
特征根性质 ❖ 特征根称为电路的固有频率,它将确定零输入响应的 形式。由于R、L、C数值不同,固有频率sl和s2可出现 三种不同的情况: 12 ( ) ( ) ( ) L LC R L LC R L LC R 1 2 3 1 2 2 1 2 1 2 2 2 = sl和s2为不相等的负实数; sl和s2为相等的负实数; sl和s2为共轭复数,实部为负; L LC R L R s 1 2 2 2 1,2 − = −

固有频率为不相等的负实数 冬当 即R>4号 时,固有频率为不相等的 负实数,齐次方程的解答可表为 uc(t)=K ev +Kex 其中常数K和K2由初始条件确定: uc(O)=K]+K2 %礼=点+K-O =[@- C K2= [- 13
固有频率为不相等的负实数 ❖ 当 即 时,固有频率为不相等的 负实数,齐次方程的解答可表为 13 L LC R 1 2 2 C L R 4 2 ( ) s t s t C u t K e K e 1 2 = 1 + 2 其中常数K1和K2由初始条件确定: ( ) ( ) ( ) ( ) ( ) ( ) − − = − − = = + = = + C i s u s s K C i s u s s K C i K s K s dt du u K K L C L C C L C 0 0 1 0 0 1 0 0 1 1 2 2 2 2 1 1 1 1 2 2 0 1 2 |

方程的解 由于5和s2是不相等的负实数,故它们可表示为 S1=一CX1 S2=-C2 =是c 可得: = 0e”-ae小49ct-e叫 02-01 i,☑=ce agg-g0e-ag dt 02-01 为随时间衰减的指数函数,表明电路响应是非振荡的。 14
方程的解 ❖ 由于sl和s2是不相等的负实数,故它们可表示为 14 L LC R L R s s 1 2 2 2 1 2 1 1 2 2 − = = − = − , ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) C t t L t t C L C t t L t t C e e i e e u C dt du i t C e e C i e e u u t 2 1 2 1 1 2 1 2 2 1 2 1 2 1 1 2 2 1 2 1 2 1 0 0 0 0 − − − − − − − − − − − + − = = − − − + − = 可得: 为随时间衰减的指数函数,表明电路响应是非振荡的
说明 当uc(0)=U,i(0)=0时,由于,< f() ,ea2t比ealt衰减的快,电流始 终为负值,说明电容电压的变化率 始终为负值,电容电压始终单调地 下降,电容自始至终在放电,最后,副 电压、电流均趋于零。 ?由于电流的初始值和稳态值均为 零,因此在某一时刻tm电流达到 一个最大值,即 d =0→,e-a2e=0 dt 1 In dz 02-1 a (b) 15
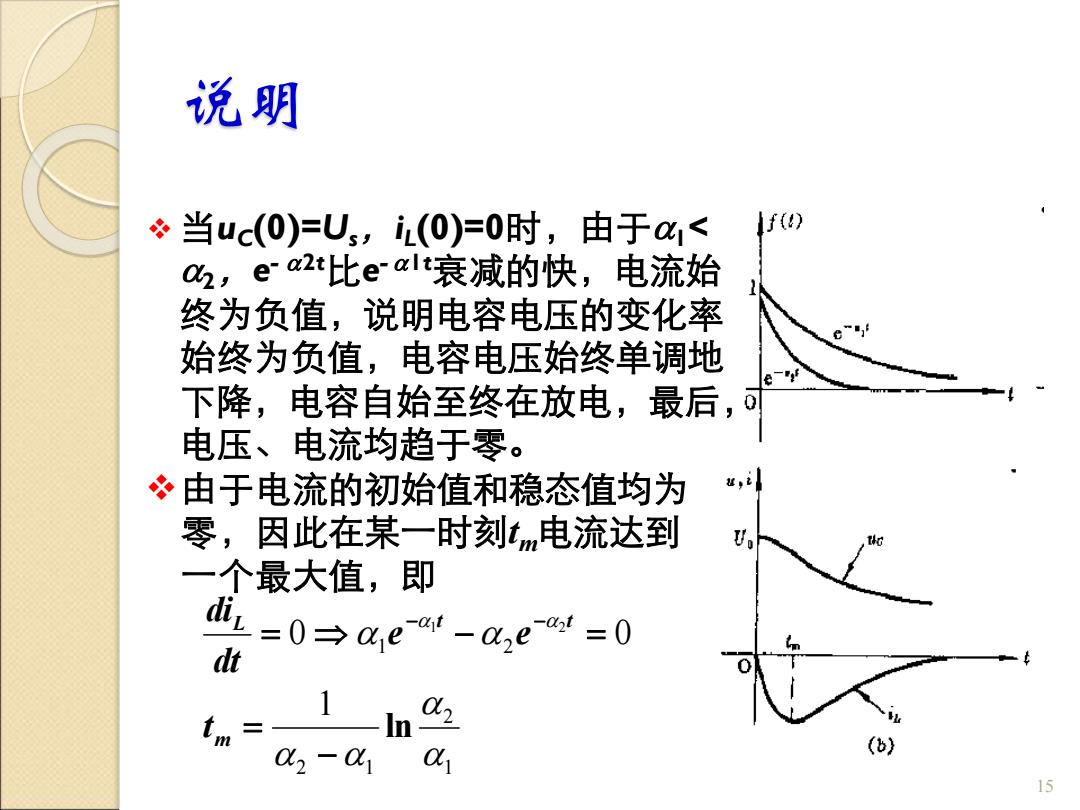
说明 ❖ 当uC(0)=Us,iL (0)=0时,由于1< 2,e - 2t比e - 1t衰减的快,电流始 终为负值,说明电容电压的变化率 始终为负值,电容电压始终单调地 下降,电容自始至终在放电,最后, 电压、电流均趋于零。 15 ❖由于电流的初始值和稳态值均为 零,因此在某一时刻tm电流达到 一个最大值,即 1 2 2 1 1 2 1 0 0 1 2 ln − = = − = − − m L t t t e e dt di