
等幅振荡和阻尼振荡 在由电容和电感两种不同的贮能元件构成的电路中, 随着贮能在电场和磁场之间的往返转移,电路中的 电流和电压将不断地改变大小和极性,形成的振荡。 1. 如果电路中不存在电阻,这种由初始贮能维持的振 荡是一种等幅振荡。 2. 如果电路中存在电阻,那么,贮能终将被电阻消耗, 振荡就不可能是等幅的,幅度将逐渐衰减而趋于零。 这种振荡称为阻尼振荡或衰减振荡。 3. 如果电阻较大,贮能在初次转移时它的大部分就可 能被电阻所消耗,因而不可能发生贮能在电场与磁 场间的往返转移现象。 6
等幅振荡和阻尼振荡 ❖ 在由电容和电感两种不同的贮能元件构成的电路中, 随着贮能在电场和磁场之间的往返转移,电路中的 电流和电压将不断地改变大小和极性,形成的振荡。 1. 如果电路中不存在电阻,这种由初始贮能维持的振 荡是一种等幅振荡。 2. 如果电路中存在电阻,那么,贮能终将被电阻消耗, 振荡就不可能是等幅的,幅度将逐渐衰减而趋于零。 这种振荡称为阻尼振荡或衰减振荡。 3. 如果电阻较大,贮能在初次转移时它的大部分就可 能被电阻所消耗,因而不可能发生贮能在电场与磁 场间的往返转移现象。 6

LC回路中振荡的简单的分析 已知L=IH、C=IF,uc(O)=IV、i(O)=0。r 根据元件的VAR可得 duc=-i, diL二uc dt dt 这是一个二阶电路,由两个联立的一阶微分方程描述, 它表明电压的存在要求有电流的变化;电流的存在要求 有电压的变化。因此电压、电流都必须处于不断的变化 状态之中。 d'uc +uc =0 dt2 结合到初始条件:uc(0)=1V,i(0)=0 7
LC回路中振荡的简单的分析 已知 L=1H、C=1F,uC(0)=1V、iL (0)=0。 7 根据元件的VAR可得 C L L C u dt di i L dt du C = − , = 这是一个二阶电路,由两个联立的一阶微分方程描述, 它表明电压的存在要求有电流的变化;电流的存在要求 有电压的变化。因此电压、电流都必须处于不断的变化 状态之中。 0 2 2 + C = C u dt d u 结合到初始条件:uC(0)=1V、iL (0)=0

LC回路中的贮能 可以得到 uc(t)=cost i,(t)=sint LC回路中的等幅振荡是按正弦方式随时间变化的。LC 回路中的贮能为 w0-0+0a回 -6m1+cow0- 常量 w(O)-jLi(O)-iCa()-iJ 表明:贮能不断地在电场和磁场之间往返,永不消失。 8
LC回路中的贮能 可以得到 8 ( ) i (t) t u t t L C sin cos = = LC回路中的等幅振荡是按正弦方式随时间变化的。LC 回路中的贮能为 ( ) ( ) ( ) ( t t) J w t Li t Cu t 2 1 sin cos 2 1 2 1 2 1 2 2 2 2 = + = = + 常量 w( ) Li ( ) Cu ( ) J 2 1 0 2 1 0 2 1 0 2 2 = + = 表明:贮能不断地在电场和磁场之间往返,永不消失
§7-2RLC串联电路的零输入响应 —过阻尼情况 冬对电感和电容的二阶电路,运 用戴维南定理可得图(b)所示的 含源屯 阻网络 RLC串联电路。 ÷对每一元件,可以写出VAR为 i=C duc dt ug =Ri=RC duc dt u L =LC (b} dt dr 冬根据KL可得 +败资+=.0 LC 0
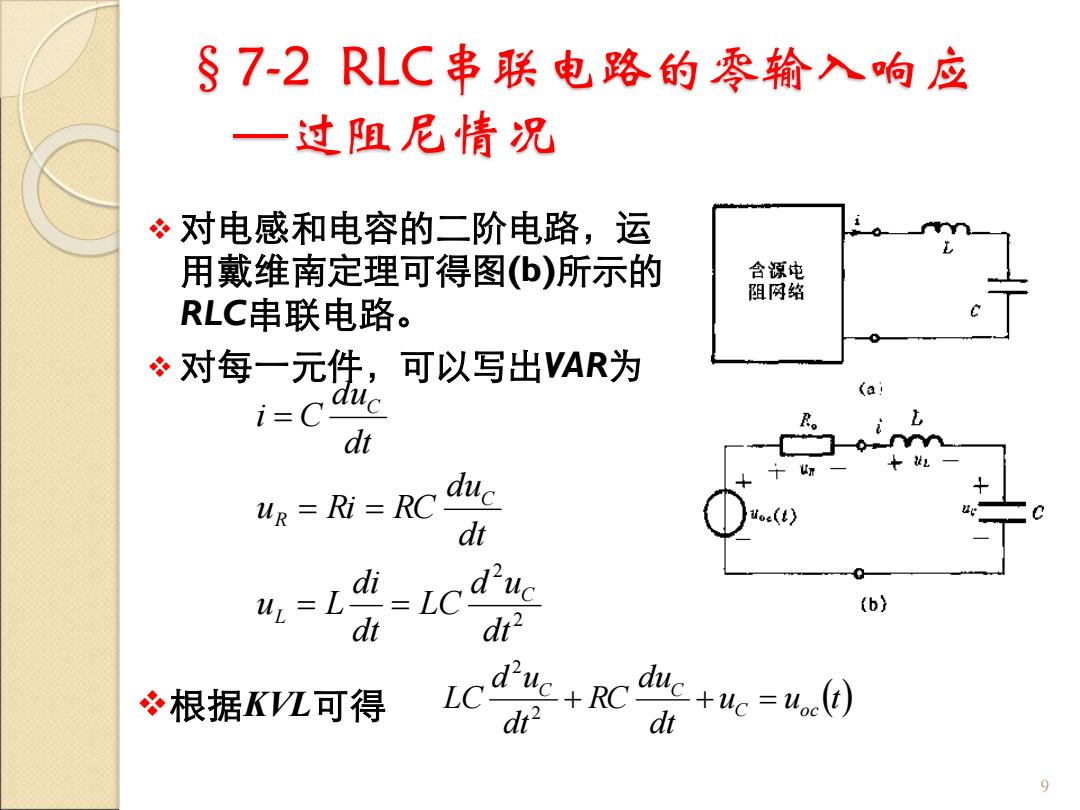
§7-2 RLC串联电路的零输入响应 —过阻尼情况 ❖ 对电感和电容的二阶电路,运 用戴维南定理可得图(b)所示的 RLC串联电路。 ❖ 对每一元件,可以写出VAR为 9 2 2 dt d u LC dt di u L dt du u Ri RC dt du i C C L C R C = = = = = ❖根据KVL可得 u u (t) dt du RC dt d u LC C oc C C + + = 2 2

初始条件 Lcwe+Rce+We=u dt dt 这是一个线性二阶常系数常微分方程,未知量为uc(t)。 为求解答此微分方程,必须知道两个初始条件,即 uc(O)以及uc'(0). uc(O)为电容的初始状态,uc(O)为: 10
初始条件 ❖ 这是一个线性二阶常系数常微分方程,未知量为uC(t)。 为求解答此微分方程,必须知道两个初始条件,即 uC(0)以及uC ’ (0)。 ❖ uC(0)为电容的初始状态,uC ’ (0)为: 10 u u (t) dt du RC dt d u LC C o c C C + + = 2 ( ) ( ) ( ) ( ) C i C i t dt du t u C C 0 0 | | 0 0 ' = = =