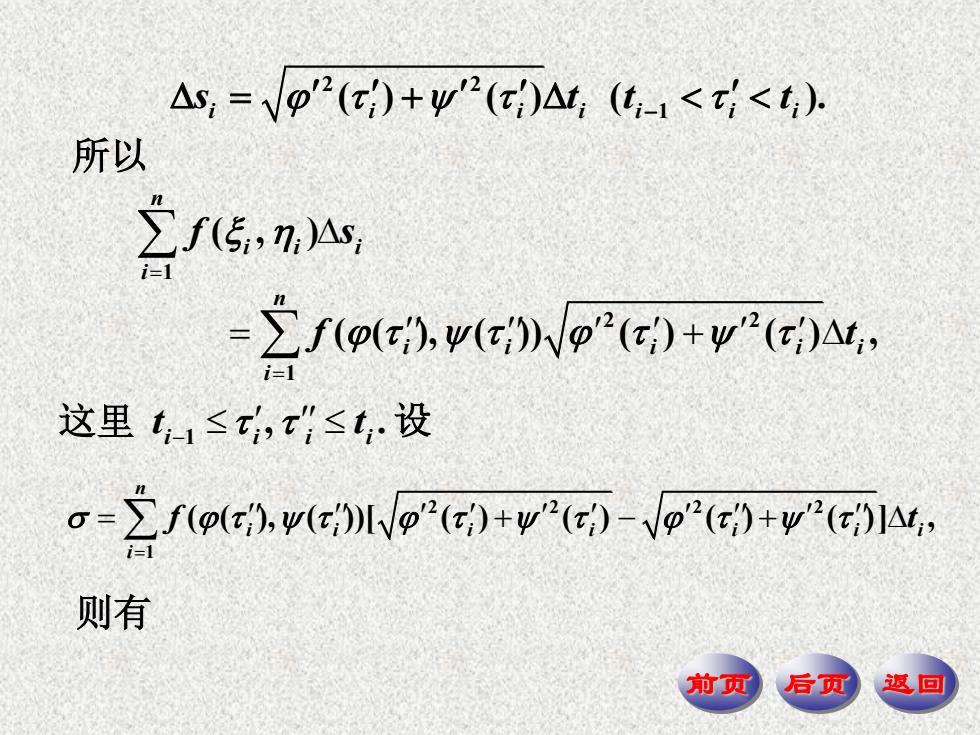
△s,=√p2()+w2()△1,(-1<<t) 所以 之f57w 2fpwor()y. 这里t1≤,t{≤t设 o->f(o()v(lo()+v"(-()+v"()A i=1 则有 前页 后页 返回
前页 后页 返回 2 2 1 ( ) ( ) ( ). i i i i i i i s t t t 1 ( , ) n i i i i f s 2 2 1 ( ( ), ( )) ( ) ( ) , n i i i i i i f t 2 2 2 2 1 ( ( ), ( ))[ ( ) ( ) ( ) ( )] , n i i i i i i i i f t 所以 1 , . i i i i 这里 t t 设 则有

会% =∑f@(,w(cp2(1+w(r)4+o.4④ 令△t=max{A,△,,△,则当T→0时,必有 △t→0.现在证明imo=0. Λt0 因为复合函数f(p(t),y(t)关于t连续,所以在闭区 间[a,B]上有界,即存在常数M,使对一切t∈[a,B] 都有 前页 后页 返回
前页 后页 返回 1 ( , ) n i i i i f s 2 2 1 ( ( ), ( )) ( ) ( ) . (4) n i i i i i i f t 令 max{ , , , }, 0 , 1 2 n t t t t T 则当 时 必有 t 0. 0 lim 0. t 现在证明 因为复合函数 f t t t ( ( ), ( )) 关于 连续, 所以在闭区 间 [ , ] 上有界, 即存在常数 M, 使对一切 t [ , ] 都有

If(o(t),v(t)M. 再由√o2()+y2(t)在[a,1上连续,所以它在 [a,B]上一致连续,即对任给的ε>0,必存在δ>0, 使当△t<6时, V@(1+y2(c-Vp2(0+y2()<c, 从而 |oKsM∑A,=eM(b-m), i-1 所以imo=0. 前页 后页 返回
前页 后页 返回 | ( ( ), ( )) | . f t t M 2 2 再由 ( ) ( ) [ , ] t t 在 上连续, 所以它在 [ , ] 上一致连续, 即对任给的 0, 必存在 0, 使当 t 时, 2 2 2 2 ( ) ( ) ( ) ( ) , i i i i 从而 1 | | ( ), n i i M t M b a 所以 0 lim 0. t

再由定积分定义 mf(v(("( =f@(),y)Np'(0+y2()dt. 因此当在(4)式两边取极限后,即得所要证的3)式. 当曲线L由方程y=V(x),x∈[4,b]表示,且w(x)在 [,b]上有连续的导函数时,(3)式成为 Sf(x,y)ds=[f(x.v(x)1+v(x)dx; 前页
前页 后页 返回 2 2 0 1 lim ( ( ), ( )) ( ) ( ) n i i i i i t i f t 2 2 ( ( ), ( )) ( ) ( )d . b a f t t t t t 因此当在(4)式两边取极限后, 即得所要证的(3)式. [ , ] a b 上有连续的导函数时, (3)式成为 2 ( , )d ( , ( )) 1 ( )d ; b L a f x y s f x x x x 再由定积分定义 当曲线 L 由方程 y x x a b ( ), [ , ] 表示, 且 ( ) x 在

当曲线L由方程x=p(y),y∈[c,d表示,且p(y)在 [c,d上有连续导函数时,(3)式成为 ∫fx,ds=fo0,yW1+pd. 例1设L是半圆周 L:0ss元 y=asint, 试计算第一型曲线积分∫x2+y)ds。 解∫2(x2+y)ds-a2Va2cos2t+sin2t0d=wn. 前页 后页 返回
前页 后页 返回 [ , ] c d 上有连续导函数时, (3)式成为 2 ( , )d ( ( ), ) 1 ( )d . d L c f x y s f y y y y 例1 设 L 是半圆周 cos , : 0 π, sin , x a t L t y a t 试计算第一型曲线积分 2 2 ( )d . L x y s 解 π 2 2 2 2 2 2 3 0 ( )d (cos sin )d π. L x y s a a t t t a 当曲线 L由方程 x y y c d ( ), [ , ] 表示, 且 在 ( ) y