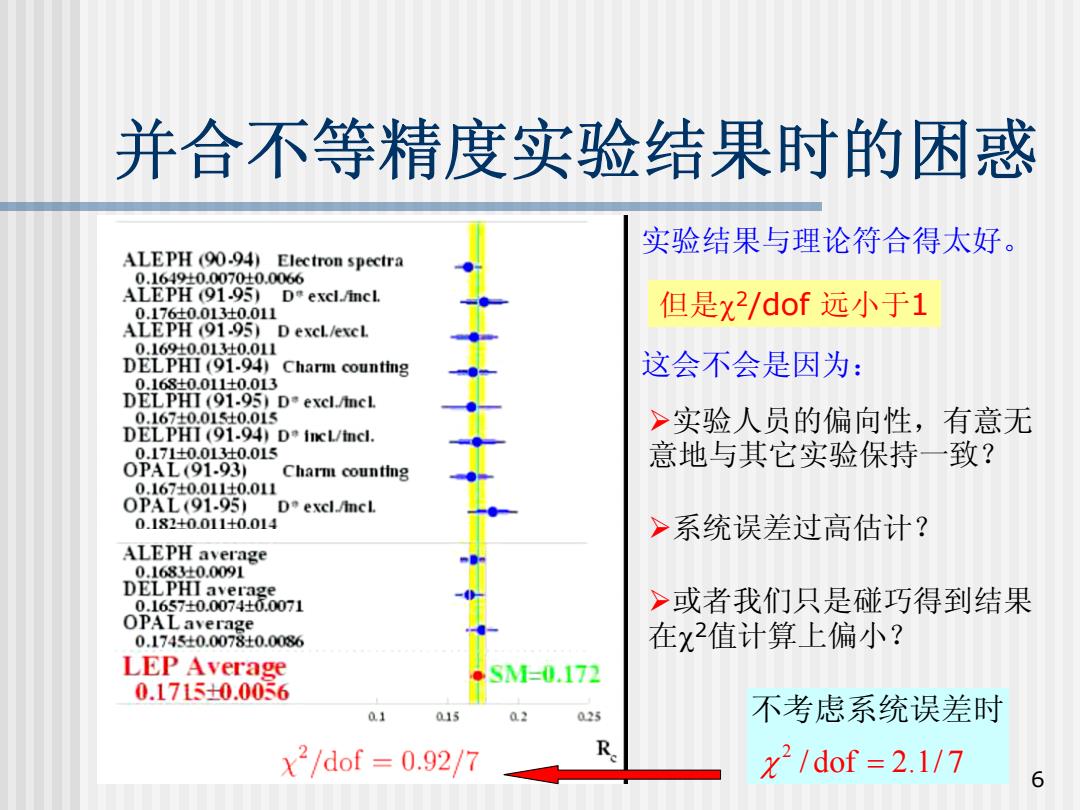
并合不等精度实验结果时的困惑 实验结果与理论符合得太好。 ALEPH (90.94)Electron spectra 0.164910.0070吐0.0066 ALEPH (91-95)D*excl./incL 0.176±0.01340.011 但是x2/dof远小于1 ALEPH (91-95)D excL/excL 0.1690.013±0.011 DELPHI (91-94)Charm counting 这会不会是因为: 0.168±0.011±0.013 DELPHI(91-95)D"excl./ineL 0.1670.015±0.015 DELPHI (91-94)D*incL/tnel. >实验人员的偏向性,有意无 0.171±0.0130.015 意地与其它实验保持一致? 0PAL(91.93) Charm counting 0.167±0.011±0.011 OPAL(91-95)D"excl./mcL 0.182+0.011±0.014 >系统误差过高估计? ALEPH average 0.1683±0.0091 DELPHI average 0.1657±0.0074±0.0071 >或者我们只是碰巧得到结果 OPALaverage 0.1745±0.0078±0.0086 在x2值计算上偏小? LEP Average SMi=0.172 0.1715±0.0056 015 023 不考虑系统误差时 x2/dof=0.92/7 x21dof=2.1/7 6
6 并合不等精度实验结果时的困惑 实验结果与理论符合得太好。 这会不会是因为: ¾实验人员的偏向性,有意无 意地与其它实验保持一致? ¾系统误差过高估计? ¾或者我们只是碰巧得到结果 在 χ 2值计算上偏小? 但是 χ 2/dof 远小于 1 2 χ / dof = 2.1 / 7 不考虑系统误差时
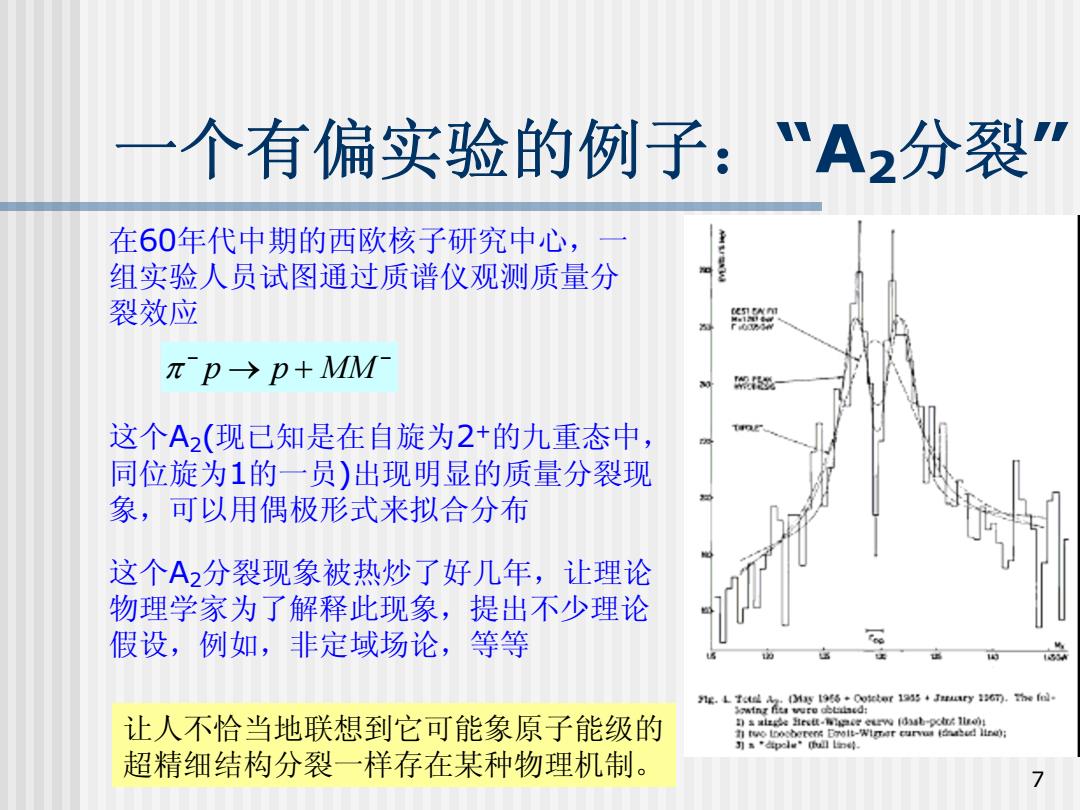
一个有偏实验的例子:"A2分裂” 在60年代中期的西欧核子研究中心, 组实验人员试图通过质谱仪观测质量分 裂效应 πp→p+MM 这个A2(现已知是在自旋为2+的九重态中, 同位旋为1的一员)出现明显的质量分裂现 象,可以用偶极形式来拟合分布 这个A2分裂现象被热炒了好几年,让理论 物理学家为了解释此现象,提出不少理论 假设,例如,非定域场论,等等 wing ft vuro o企aed: 让人不恰当地联想到它可能象原子能级的 目s alngbe Hrvtt-49 ce eurw idab-g在k1lne0: 3月s”2le”国n4 超精细结构分裂一样存在某种物理机制
7 一个有偏实验的例子:“A 2分裂 ” 在60年代中期的西欧核子研究中心,一 组实验人员试图通过质谱仪观测质量分 裂效应 π p p MM − − → + 这个 A 2 (现已知是在自旋为 2 +的九重态中, 同位旋为 1的一员 )出现明显的质量分裂现 象,可以用偶极形式来拟合分布 这个 A 2分裂现象被热炒了好几年,让理论 物理学家为了解释此现象,提出不少理论 假设,例如,非定域场论,等等 让人不恰当地联想到它可能象原子能级的 超精细结构分裂一样存在某种物理机制

A2分裂”例子(续) 但是,此后类似的几个实验均未发现任何这种质量分裂效应 另外一些别的实验通过A)衰变到不同的K+K模式,也没有发现任何质量 分裂的现象 最后在1971年华盛顿美国物理学会年会上,该实验的发言人宣布所观测 到的质量分裂结果是由几个没有必要的事例选择条件人为造成的 其中的一个选择条件是与实验运行条件"有关。当拿掉该选择条件以后, 再也看不到质量分裂效应了 这个例子被广泛任为是“无辜偏向性“的受害者 在粒子物理与核物理实验研究中,历史上类似的无辜偏向性“受害者 很多。为了避免这种情况的发生,近几年来盲分析方法渐渐成为潮流。 8
8 “A2分裂”例子(续) 但是,此后类似的几个实验均未发现任何这种质量分裂效应 另外一些别的实验通过A2衰变到不同的K+K-模式,也没有发现任何质量 分裂的现象 最后在1971年华盛顿美国物理学会年会上,该实验的发言人宣布所观测 到的质量分裂结果是由几个没有必要的事例选择条件人为造成的 其中的一个选择条件是与“实验运行条件”有关。当拿掉该选择条件以后, 再也看不到质量分裂效应了 这个例子被广泛任为是“无辜偏向性”的受害者 在粒子物理与核物理实验研究中,历史上类似的“无辜偏向性”受害者 很多。为了避免这种情况的发生,近几年来盲分析方法渐渐成为潮流

盲分析方法分类 信号区隐藏法 •最适合于对稀有或禁戒物理过程的实验测量; ·本底必须从非信号区、或模拟样本、或额外的子实验来估计。 偏置法 •适合于单值测量(例如,测量不对称性),而且, 统计误差已经不是 实验上的决定因素; •拟合量中包含随机的符号与偏置: 分解法 •将实验分解为对若干个子测量量的研究而不看最终结果; ·最终结果为各不同子测量量的计算总汇(例如,μ-子磁矩测量中, 分别测量μ-子的进动频率与回旋频率差和磁场大小,最后得到子 磁矩的测量值) 9
9 盲分析方法分类 信号区隐藏法 偏置法 分解法 •最适合于对稀有或禁戒物理过程的实验测量; •本底必须从非信号区、或模拟样本、或额外的子实验来估计。 •适合于单值测量 (例如,测量不对称性 ),而且,统计误差已经不是 实验上的决定因素; •拟合量中包含随机的符号与偏置; •将实验分解为对若干个子测量量的研究而不看最终结果; •最终结果为各不同子测量量的计算总汇 (例如, μ -子磁矩测量中, 分别测量 μ -子的进动频率与回旋频率差和磁场大小,最后得到 μ - 子 磁矩的测量值 )