得(1-7)式的分子 ∈oe-neo/kT (1-e-neo/kr2,所以 Es∈oe-eo/kr (1-e-eo/kr7(1-e)= Eo eEo/kT-1 C。再将这个平均能量乘以空腔单位体积内频率D到+d山之间的振动数目8 8πV2 c3dv,得到黑体辐射能量分 布公式 8πv2∈0 p(v,7)dv-c3 eo/kr-1dv (1-9) 此式与Wien由热力学得出公式(1-4)比较,可以看出∈o必须与振子的固有频率v成正比 Eo=hv (0-10) h是Planck常数, h=6.62559×1034J·s P(v,n 图1.2黑体辐射的能量分布曲线 (R是Ravleigh-Jeans线,P是Planck线和实验曲线,W是Wien线) 将(1-10)式代入(1-9)式中,得Planck的辐射公式 1 p(v,T)dv 8πhv2 c3 ehv/kT-1dv (1-11) 公式(1-11)与实验符合得很好,见图1.2 当频率很高时,即hvkT>l,则(1-11)式分母中的1可以略去,于是得到 P(v,T)dv-8rhv2 cae-hv/kr dv 这就是Wien公式(1-4). 当频率很低时,即hvkT<<l,可利用展开式 e-hv/kT=l+hv/kT+… 取前两项,(1-11)式变为 p(v,T)dv 8πv2 c3 kIdv 这就是Rayleigh-Jeans公式(1-5). Planck能量量子化的假设如此成功地解释了黑体辐射现象,使人们不得不来重新探讨辐射的本性,尽 管辐射的波动本性为一系列实验事实所证实,例如前面讨论的光(辐射)的双缝衍射实验,但是按照Planck 的假设,在辐射过程中所发射和吸收的能量单位却是量子化的能量子w.那么可否设想能量子v具有粒子
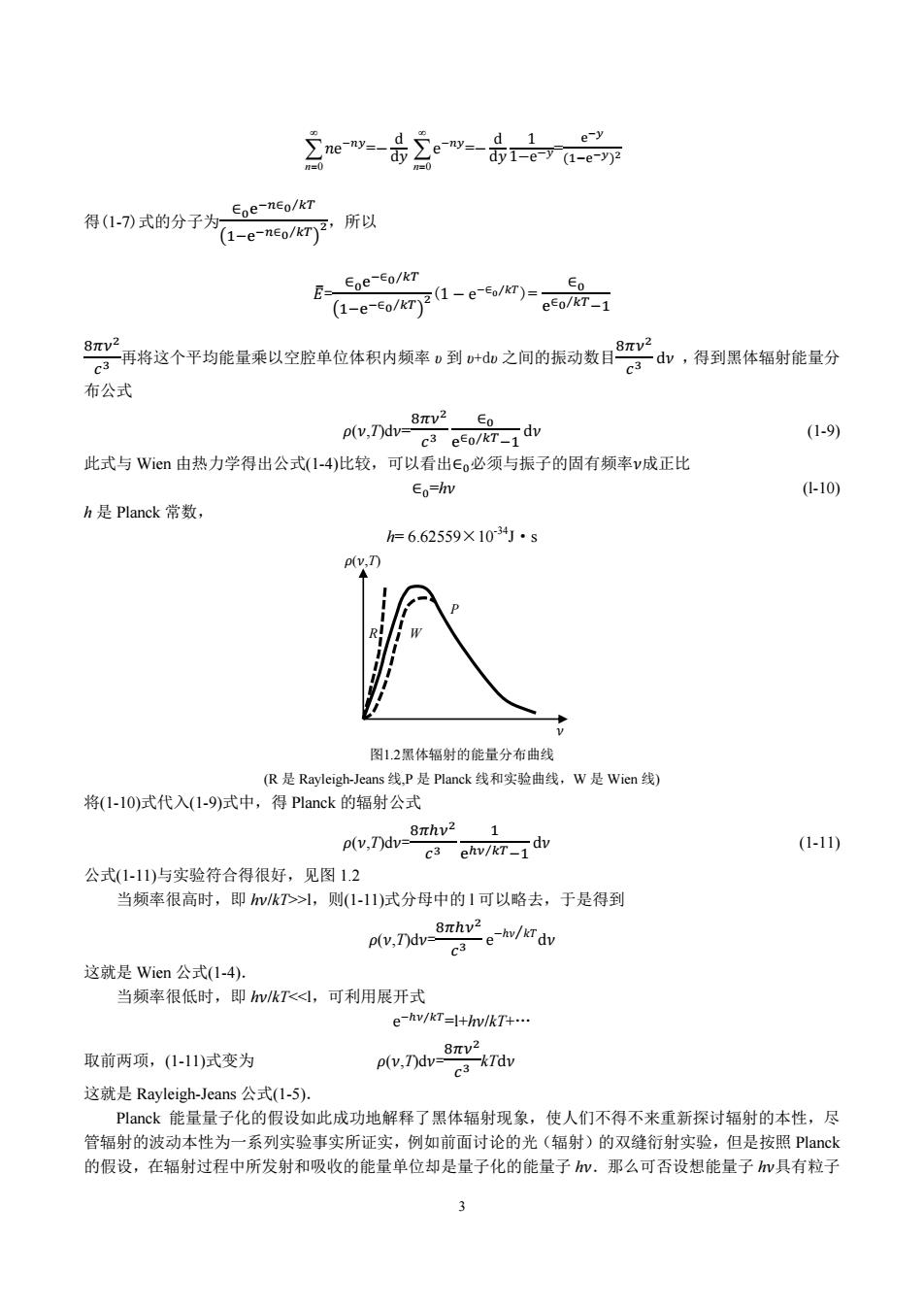
3 n0 ݊eି௬=െ d dݕ n0 eି௬=െ d ݕd 1 1െeെݕୣ =ష ሺଵିୣషሻమ 得(1-7)式的分子为 ∈బୣష∈బ⁄ೖ ൫ଵିୣష∈బ⁄ೖ൯ మ,所以 ܧത= ∈బୣష∈బ⁄ೖ ൫ଵିୣష∈బ⁄ೖ൯ మ(1െeି∈బ⁄்)= ∈బ ୣ∈బ⁄ೖିଵ ଼గఔమ య 再将这个平均能量乘以空腔单位体积内频率 υ 到 υ+dυ 之间的振动数目଼గఔమ య dߥ, 得到黑体辐射能量分 布公式 =ߥd)T,ߥ)ߩ ଼గఔమ య ∈బ ୣ∈బ⁄ೖିଵ dߥ) 1-9) 此式与 Wien 由热力学得出公式(1-4)比较,可以看出∈必须与振子的固有频率ߥ成正比 ∈=hߥ) l-10) h 是 Planck 常数, h= 6.62559×10-34J·s (T,ߥ)ߩ P R W ߥ 图1.2黑体辐射的能量分布曲线 (R 是 Rayleigh-Jeans 线,P 是 Planck 线和实验曲线,W 是 Wien 线) 将(1-10)式代入(1-9)式中,得 Planck 的辐射公式 =ߥd)T,ߥ)ߩ ଼గఔమ య ଵ ୣഌ ೖ ⁄ ିଵ dߥ) 1-11) 公式(1-11)与实验符合得很好,见图 1.2 当频率很高时,即 hߥ/kT>>l,则(1-11)式分母中的 l 可以略去,于是得到 =ߥd)T,ߥ)ߩ ଼గఔమ య e ߥd ݇ܶ ⁄ ߥ݄െ 这就是 Wien 公式(1-4). 当频率很低时,即 hߥ/kT<<l,可利用展开式 eିఔ ் ⁄ =l+hߥ/kT+… 取前两项,(1-11)式变为 ߩ)ߥ,T)dߥ= ଼గఔమ య kTdߥ 这就是 Rayleigh-Jeans 公式(1-5). Planck 能量量子化的假设如此成功地解释了黑体辐射现象,使人们不得不来重新探讨辐射的本性,尽 管辐射的波动本性为一系列实验事实所证实,例如前面讨论的光(辐射)的双缝衍射实验,但是按照 Planck 的假设,在辐射过程中所发射和吸收的能量单位却是量子化的能量子 hߥ.那么可否设想能量子 hߥ具有粒子

的某些性质呢?这一问题留待下一节讨论 1.2 辐射的粒子性 首先肯定光除了波动性之外还有粒子性的是爱因斯坦(Einstein).他认为电磁辐射不仅在被发射和吸收 时以能量为的粒子形式出现,而且以这种形式在空间以速度c运动.这种粒子叫做光量子或光子,用这 个观点,Einstein成功地解释了光电效应. 1.2.1光电效应 光电效应是当光照射到金属上时,有电子从金属表面逸出。这种电子称为光电子,实验表明,只有当 光的频率大于某一阈值时,才有光电子发射出来;如果光的频率低于这个阈值,则无论光的强度多大、照 射时间多长,都没有光电子产生,光的频率越高,光电子的能量就越大,光的强度只影响光电子的数目, 而与光电子的能量无关,光电效应的这些规律是经典理论所无法解释的.按照光的电磁理论,光的能量只 决定于光的强度而与光的频率无关。 按照Einstein的光子学说,当光照射到金属表面时,能量为w的光子被电子所吸收,电子把这能量的 一部分用作为它脱出金属表面所消耗的功%(称为脱出功),另一部分就是电子离开金属后的动能乏心, 即 2Mv2-hv-Wo 1 (1-12) 如果电子所吸收的光子能量w小于W,则电子不能脱出金属表面,因而没有光电子产生.光的频率决 定光子的能量,光的强度只决定光子的数目,光子多,产生的光电子也多,这样,经典理论所不能解释的 光电效应就得到了圆满的说明. 光子不但具有能量,而且具有动量.按照相对论关系式,以速度ⅴ运动的粒子,其能量为 E=uoc2/1-v2/c2 式中o为粒子的静止质量,对于光子,=℃.光子的能量总是有限的,所以由上式得到光子的静止质量为零, 由相对论中能量和动量的关系式 E2=uoc+c2p2 可得到光子的能量E和动量P的关系是E=cP,由光子的能量 E=hv (1-13) 可得到光子的动量为 P=h/a (1-14) 按照Einstein的光子学说,光是一束以光速c行进的光子流,光的强度取决于单位体积内的光子数目, 即取决于光子的密度,空间中某点的光子密度为 p=dN/dv (1-15) 式中dW为体积元dv内的光子数目. 1.2.2康普顿(Compton)效应 Compton效应的发现,进一步证实了光具有粒子性.实验发现,高频率的X射线被轻元素中的电子散 射后,波长随散射角的增加而增大,按照经典电动力学,电磁波被散射后波长不应改变,如果把这个过程 看作是光子与电子的碰撞过程,则可圆满解释Compton效应. Compton效应如图1.3所示,其中w和hv',分别表示光子在碰撞前后的能量,由此得光于碰撞前的动
4 的某些性质呢?这一问题留待下一节讨论. 1.2 辐射的粒子性 首先肯定光除了波动性之外还有粒子性的是爱因斯坦(Einstein).他认为电磁辐射不仅在被发射和吸收 时以能量为 hߥ的粒子形式出现,而且以这种形式在空间以速度 c 运动.这种粒子叫做光量子或光子,用这 个观点,Einstein 成功地解释了光电效应. 1.2.1 光电效应 光电效应是当光照射到金属上时,有电子从金属表面逸出。这种电子称为光电子.实验表明,只有当 光的频率大于某一阈值时,才有光电子发射出来;如果光的频率低于这个阈值,则无论光的强度多大、照 射时间多长,都没有光电子产生,光的频率越高,光电子的能量就越大,光的强度只影响光电子的数目, 而与光电子的能量无关,光电效应的这些规律是经典理论所无法解释的.按照光的电磁理论,光的能量只 决定于光的强度而与光的频率无关. 按照 Einstein 的光子学说,当光照射到金属表面时,能量为 hߥ的光子被电子所吸收,电子把这能量的 一部分用作为它脱出金属表面所消耗的功 W0(称为脱出功),另一部分就是电子离开金属后的动能ଵ ݒߤ ଶ 2 , 即 ଵ ݒߤ ଶ 2 =hߥെW0 (1-12) 如果电子所吸收的光子能量 hߥ小于 W0,则电子不能脱出金属表面,因而没有光电子产生.光的频率决 定光子的能量,光的强度只决定光子的数目,光子多,产生的光电子也多.这样,经典理论所不能解释的 光电效应就得到了圆满的说明. 光子不但具有能量,而且具有动量.按照相对论关系式,以速度 v 运动的粒子,其能量为 E=ߤܿଶ ඥ1െߥଶ ܿ ⁄ ⁄ ଶ 式中ߤ为粒子的静止质量,对于光子,v=c.光子的能量总是有限的,所以由上式得到光子的静止质量为零, 由相对论中能量和动量的关系式 E2 ߤ= ଶc 4 +c2 P2 可得到光子的能量 E 和动量 P 的关系是 E=cP,由光子的能量 E=hߥ) 1-13) 可得到光子的动量为 P=h/ߣ) 1-14) 按照 Einstein 的光子学说,光是一束以光速 c 行进的光子流,光的强度取决于单位体积内的光子数目, 即取决于光子的密度,空间中某点的光子密度ߩ为 ߩ =dN/dv (1-15) 式中 dN 为体积元 dv 内的光子数目. 1.2.2 康普顿(Compton)效应 Compton 效应的发现,进一步证实了光具有粒子性.实验发现,高频率的 X 射线被轻元素中的电子散 射后,波长随散射角的增加而增大,按照经典电动力学,电磁波被散射后波长不应改变,如果把这个过程 看作是光子与电子的碰撞过程,则可圆满解释 Compton 效应. Compton 效应如图 1.3 所示,其中 hߥ和݄ߥ,′分别表示光子在碰撞前后的能量,由此得光于碰撞前的动

量为ha h hv y 碰撞后的动量为 ,电子碰撞前静止,碰撞后速度为ⅴ,若电子的静止质量为μ,则根 c/v c 据相对论,电子碰撞后的动能为 E- Hoc2 1-b2/c2 动量为 P= 1-2/c2 由于碰撞前后能量守恒、动量的x和y分量分别守恒,因而有 hv=hv'+Ec (能量守恒) hvhv -cos0+P.cos0" (动量的x分量守恒) (1-16) CC sin0+P sin0' (动量的y分量守恒) 2h.20 由此方程组可解出 △1='-1 sin- uc 2 式中号号 上式由Compton首先提出,由Compton和吴有训用实验证实,这样,用光的微粒性就解 释了Compton效应. hv e 图1.3 Compton效应 1.2.3辐射的波粒二象性 Planck和Einstein理论揭示出光的微粒性,并用这一理论可以定量地解释光电效应和Compton效应, 而经典的波动理论却无法说明这些现象,但是对另外一些现象,例如光的干涉和衍射,可用波动理论定量 地解释之,而微粒理论则无能为力.由此可以得出结论:辐射(包括光)具有微粒和波动的双重性质,这 种性质称为波粒二象性。 究竞辐射表现其波动性还是粒子性,这要由实验类型来决定,如果辐射与物质相互作用,并在物质中 引起可测量到的变化(例如引起电子的发射),辐射往往显示其粒子性:如果辐射与物质相互作用,并使 辐射在空间的分布发生可测量到的变化(例如狭缝衍射),而并未在物质中引起可测量到的变化,辐射往 往显示其波动性。 关系式(1-13)和(1-14)把辐射的两重性质一一波动性和粒子性一一联系了起来,式中的能量和动量是描述其 粒子性的,而波长和频率是描述其波动性的.由这两个关系式还可以看出Planck常数h在微观现象中所占 的重要地位,能量和动量的量子化是通过h这个小量而表现出来的,在宏观现象中,h这一小量的作用实在 微不足道,以至于能量和动量的量子化完全可以忽略,把这些量视为连续变化是足够精确的,因此,凡是h 在其中起重要作用的现象都可称为量子现象,相应地应该用量子理论来处理,若用经典理论处理则会导致
5 量为 h/ߣ = ఔ⁄ = ఔ ,碰撞后的动量为ఔᇲ ,电子碰撞前静止,碰撞后速度为 v,若电子的静止质量为ߤ,则根 据相对论,电子碰撞后的动能为 E= ఓబమ ඥଵି௩మ ⁄ మ െ ߤܿ 2 动量为 P= ఓఔ ඥଵି௩మ ⁄ మ 由于碰撞前后能量守恒、动量的 x 和 y 分量分别守恒,因而有 hߥ݄=ߥ+′Ec (能量守恒) ఔ = ఔᇲ cosθ+Pccosθ' (动量的 x 分量守恒) (1-16) 0= ఔᇲ sinθ+Pcsinθ' (动量的 y 分量守恒) 由此方程组可解出 Δߣ=ߣᇱ െ ߣ= ଶ ఓ sin2ఏ ଶ 式中ߣᇱ = ఔᇲ =ߣ , ఔ .上式由 Compton 首先提出,由 Compton 和吴有训用实验证实,这样,用光的微粒性就解 释了 Compton 效应. y ′ߥ݄ x ߠ ߥ݄ ′ߠ v e - 图 1.3 Compton 效应 1.2.3 辐射的波粒二象性 Planck 和 Einstein 理论揭示出光的微粒性,并用这一理论可以定量地解释光电效应和 Compton 效应, 而经典的波动理论却无法说明这些现象,但是对另外一些现象,例如光的干涉和衍射,可用波动理论定量 地解释之,而微粒理论则无能为力.由此可以得出结论:辐射(包括光)具有微粒和波动的双重性质,这 种性质称为波粒二象性。 究竟辐射表现其波动性还是粒子性,这要由实验类型来决定,如果辐射与物质相互作用,并在物质中 引起可测量到的变化(例如引起电子的发射),辐射往往显示其粒子性;如果辐射与物质相互作用,并使 辐射在空间的分布发生可测量到的变化(例如狭缝衍射),而并未在物质中引起可测量到的变化,辐射往 往显示其波动性。 关系式(1-13)和(1-14)把辐射的两重性质——波动性和粒子性——联系了起来,式中的能量和动量是描述其 粒子性的,而波长和频率是描述其波动性的.由这两个关系式还可以看出 Planck 常数 h 在微观现象中所占 的重要地位,能量和动量的量子化是通过 h 这个小量而表现出来的,在宏观现象中,h 这一小量的作用实在 微不足道,以至于能量和动量的量子化完全可以忽略,把这些量视为连续变化是足够精确的,因此,凡是 h 在其中起重要作用的现象都可称为量子现象,相应地应该用量子理论来处理,若用经典理论处理则会导致

荒谬的结论. 1.3关于原子结构的早期理论 1.3.1电子的确定 电子作为一个粒子的概念应追溯到法拉第(Faraday)的电解电池实验.他发现电极上电解出的物质质量与 通过电池的电量成正比,而且当不同的电池串联时,各电池析出的产物都有相等的当量数.Faraday由这些 实验所得出的结论是:相等当量的物质(如1克氢,8克氧,118克银)含有相等的电量.1891年,斯托尼 (Stoney)提出用“电子”这一名称来表示电量的单位,在l897年前后,J.J.Thomson用阴极射线管的实验, 由射线在电场和磁场中的偏转,测定了电子的电荷和质量比约为广的电荷和质量比的,1 ,从而得到电子 1840 质量约为氢原子质量的80在1S09年,密利肯RA.Milikan采用油滴实验,由运动着的带有电子的油滴 所经受的重力,电场力和空气阻力之间的关系,测定了电子电荷,从而最后证实了电子是一个带有负电荷 的粒子. 现在采用的电子电荷和质量的精确值是 e=1.6201×1019c 4=9.1091×102g 1.3.2汤姆森(Thomson)的原子模型 因为原子的质量为1022一1024g,比电子的质量大3-5个数量级,所以电子对原子质量的贡献很小.而 且,原子是电中性的,这一事实表明,原子中存在着中和电子的正电荷.另外,由动力学理论可估计出原 子的半径约为l0cm.在对原子有了这些认识的基础上,Thomson提出了一种原子模型.他认为原子的质 量和正电荷像“胶冻”一样均匀充满原子占据的空间,而电子则大致均匀地嵌在胶冻中,Thomson的原子 模型曾被称作为“胶冻”模型或“葡萄干面包”(currant bun)模型.这一模型并没有延续很长时间,因为时 隔不久新的实验表明这种模型并不正确. 1.3.3原子核的发现 I9I1年,Rutherford和他的学生盖革(Geiger)用带有两个正电荷的a粒子流轰击重金属箔时,在所有的角 度都发现有经散射后的粒子,少数α粒子的散射角为180°(与入射方向相反).相应的计算表明,若按 Thomson原子模型,a粒子的散射角不应大于90°,对这一实验结果的唯一解释是原子的质量和正电荷集中 分布在一个粒子上(即原子核上),原子核的半径约为1012cm,而运动着的电子则充满半径约为108cm的 原子空间, l.3.4卢瑟福(Rutherford)的原子模型 根据a粒子散射实验,Rutherford提出了一个原子模型.他认为原子是一个微小的太阳系,电子绕原子 核的运动相似于行星绕太阳的轨道运动。 在这一原子模型下,原子序数为Z的原子,其原子核与一个电子间的静电势能为 6
6 荒谬的结论. 1.3 关于原子结构的早期理论 1.3.1 电子的确定 电子作为一个粒子的概念应追溯到法拉第(Faraday)的电解电池实验.他发现电极上电解出的物质质量与 通过电池的电量成正比,而且当不同的电池串联时,各电池析出的产物都有相等的当量数.Faraday 由这些 实验所得出的结论是:相等当量的物质(如 1 克氢,8 克氧,118 克银)含有相等的电量.1891 年,斯托尼 (Stoney)提出用“电子”这一名称来表示电量的单位,在 1897 年前后,J.J.Thomson 用阴极射线管的实验, 由射线在电场和磁场中的偏转,测定了电子的电荷和质量比约为 H+ 的电荷和质量比的 ଵ ଵ଼ସ,从而得到电子 质量约为氢原子质量的 ଵ ଵ଼ସ。在 1909 年,密利肯(R.A.Millikan)采用油滴实验,由运动着的带有电子的油滴 所经受的重力,电场力和空气阻力之间的关系,测定了电子电荷 e,从而最后证实了电子是一个带有负电荷 的粒子. 现在采用的电子电荷和质量的精确值是 e=1.6201×10-19C μ=9.1091×10-28 g 1.3.2 汤姆森(Thomson)的原子模型 因为原子的质量为 10-22—10-24 g,比电子的质量大 3-5 个数量级,所以电子对原子质量的贡献很小.而 且,原子是电中性的,这一事实表明,原子中存在着中和电子的正电荷.另外,由动力学理论可估计出原 子的半径约为 10-8 cm.在对原子有了这些认识的基础上,Thomson 提出了一种原子模型.他认为原子的质 量和正电荷像“胶冻”一样均匀充满原子占据的空间,而电子则大致均匀地嵌在胶冻中.Thomson 的原子 模型曾被称作为“胶冻”模型或“葡萄干面包”(currant bun)模型.这一模型并没有延续很长时间,因为时 隔不久新的实验表明这种模型并不正确. 1.3.3 原子核的发现 1911 年,Rutherford 和他的学生盖革(Geiger)用带有两个正电荷的ߙ粒子流轰击重金属箔时,在所有的角 度都发现有经散射后的ߙ粒子,少数ߙ粒子的散射角为 180°(与入射方向相反).相应的计算表明,若按 Thomson 原子模型,ߙ粒子的散射角不应大于 90°,对这一实验结果的唯一解释是原子的质量和正电荷集中 分布在一个粒子上(即原子核上),原子核的半径约为 10-12 cm,而运动着的电子则充满半径约为 10-8 cm 的 原子空间. 1.3.4 卢瑟福(Rutherford)的原子模型 根据ߙ粒子散射实验,Rutherford 提出了—个原子模型.他认为原子是一个微小的太阳系,电子绕原子 核的运动相似于行星绕太阳的轨道运动。 在这一原子模型下,原子序数为 Z 的原子,其原子核与一个电子间的静电势能为

-2e2 (1-18) 式中r为核与电子的距离,一个电子所受到的核的静电引力为 -兴-码-琴 这个力应作为电子绕核作圆周运动(速度为)的向心力(假定核固定不动) uv2 Ze2 1 由此得电子的动能为 Ze2 T2w2 (1-19) 总能量为 E-T+-=-T (1-20) 2 可见电子的总能量为负值,这是因为选取了=o的点作为能量零点.关系式(1-19)或(1-20)称为virial定 1 理(virial源自拉丁文vires,原意是“力”),即总能量为平均总势能的二或平均总动能的负值,这里的virial 定理虽然是用经典理论得到的,但可以证明,在量子力学中virial定理也成立,并适用于所有原子和平衡构 型下的分子体系. 1.3.5原子结构的玻尔(Bohr)理论 一百多年以前,人们就发现了关于原子光谱的现象和规律,如原子光谱是分立的谱线,谱线的频率只 能为某些特定数值等. 在光谱实验中,常常先测定波长入,并由下式 v=clλ (1-21) 计算频率v.实际上光谱的数据一般比光速c的实验数据精确,因此为了避免不甚精确的大数c出现在光谱数 据中,在光谱学中常以波数节为单位,的定义是 必总v cm (1-22) λc 可见是单位长度(cm)中波的数目。 里德堡(Rydberg)在对氢原子光谱的研究中发现,其所有谱线都可由下式得到 11 (1-23) n1=1,2,3,…:n2=11+l,n1+2,… 式中R为Rydberg常数,其精确值为 R=1.0967758×103cm'=13.5979eV (1-24) 用Rutherford原子模型无法解释原子光谱的分立谱线,而且正像本章的开头所指出的,按经典理论 Rutherford模型是不能稳定存在的,为了解决理论和实验之间的这些矛盾,1913年,Bohr提出两点假设: 1)定态规则 原子中的电子不可能沿着经典理论所允许的每一个轨道运动,而只能沿着其中一组特殊的轨道运动, 沿着这一组特殊轨道运动的电子既不吸收也不发出辐射,即电子处于稳定状态(定态).定态的条件是:电 子作圆周运动的角动量M满足 作2元h n=1,2,3, (1-25) 显然每一个定态有一个确定的能量点。 >
7 V=െ ܼ݁2 ݎ) 1-18) 式中 r 为核与电子的距离,一个电子所受到的核的静电引力为 F=െ dܸ dݎ=െ d dݎ)െ ܼ݁2 ݎ=( െ ܼ݁2 ݎ 这个力应作为电子绕核作圆周运动(速度为 v)的向心力(假定核固定不动) ఓ௩మ =െ ܼ݁2 ݎ 由此得电子的动能为 T= ଵ ݒߤ ଶ 2 = మ ଶ =െ 1 2V (1-19) 总能量为 E=T+V= ଵ ଶ V=െT (1-20) 可见电子的总能量为负值,这是因为选取了 r=∞的点作为能量零点.关系式(1-19)或(1-20)称为 virial 定 理(virial 源自拉丁文 vires,原意是“力”),即总能量为平均总势能的ଵ ଶ 或平均总动能的负值,这里的 virial 定理虽然是用经典理论得到的,但可以证明,在量子力学中 virial 定理也成立,并适用于所有原子和平衡构 型下的分子体系. 1.3.5 原子结构的玻尔(Bohr)理论 一百多年以前,人们就发现了关于原子光谱的现象和规律,如原子光谱是分立的谱线,谱线的频率只 能为某些特定数值等. 在光谱实验中,常常先测定波长ߣ,并由下式 ߥ=c/ߣ) 1-21) 计算频率ߥ.实际上光谱的数据一般比光速 c 的实验数据精确,因此为了避免不甚精确的大数 c 出现在光谱数 据中,在光谱学中常以波数ߥ为单位,ߥ的定义是 =ߥ ଵ ఒ = ఔ cm -l (1-22) 可见ߥ是单位长度(cm)中波的数目。 里德堡(Rydberg)在对氢原子光谱的研究中发现,其所有谱线都可由下式得到 )R=ߥ ଵ భ మ െ ଵ మ మ) (1-23) n1=1, 2, 3, …;n2=n1+l, n1+2, … 式中 R 为 Rydberg 常数,其精确值为 R= 1.0967758×l05 cm -1=13.5979eV (1-24) 用 Rutherford 原子模型无法解释原子光谱的分立谱线,而且正像本章的开头所指出的,按经典理论 Rutherford 模型是不能稳定存在的,为了解决理论和实验之间的这些矛盾,1913 年,Bohr 提出两点假设: 1)定态规则 原子中的电子不可能沿着经典理论所允许的每一个轨道运动,而只能沿着其中一组特殊的轨道运动, 沿着这一组特殊轨道运动的电子既不吸收也不发出辐射,即电子处于稳定状态(定态).定态的条件是:电 子作圆周运动的角动量 M 满足 M=n ଶగ≡n n=1,2,3,… (1-25) 显然每一个定态有一个确定的能量点