
第二次分解 按照这个办法,继续把N/2用2除,由于作2M, 仍然是偶数,可以被2整除,因此可以对两个/2点 的DFT再分别作进一步的分解。即对{G()和[H()] 的计算,又可以分别通过计算两个长度为/4=2点的 DFT,进一步节省计算量。这样,一个8点的DFT就可 以分解为四个2点的DFT。 G划-答iGl2聪+脱n习e2+1略 (4)- (N4)1 (w4)-1 H[]=h[2]w4+W2h[2+1]W4
按照这个办法,继续把N/2用2除,由于N=2 M , 仍然是偶数,可以被2整除,因此可以对两个N/2点 的DFT再分别作进一步的分解。即对{G(k)}和{H(k)} 的计算,又可以分别通过计算两个长度为N/4=2点的 DFT,进一步节省计算量。这样,一个8点的DFT就可 以分解为四个2点的DFT。 第二次分解
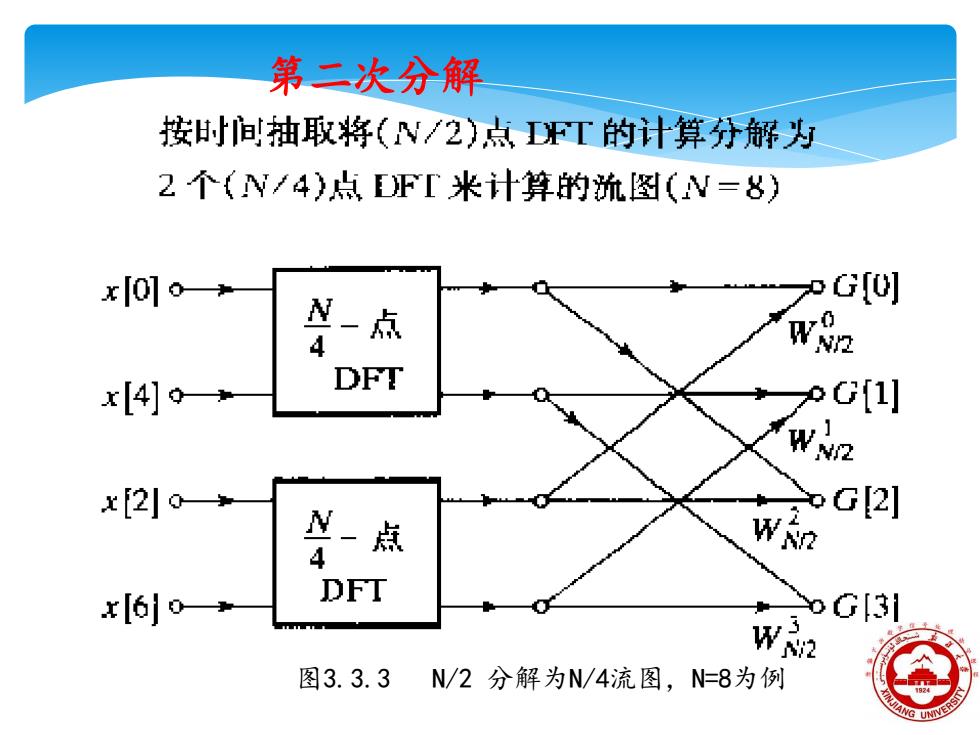
第二次分解 按时间抽取将(N/2)点FT的计算分解为 2个(N/4)点EFT米计算的流图(N=8) xI01o→ G[0] 一点 4 w82 x[4] DFT G[1] WN2 x20 Y-点 G2] 4 W x60+ DFT G[3 图3.3.3N/2分解为N/4流图,N=8为例
图3.3.3 N/2 分解为N/4流图,N=8为例 第二次分解
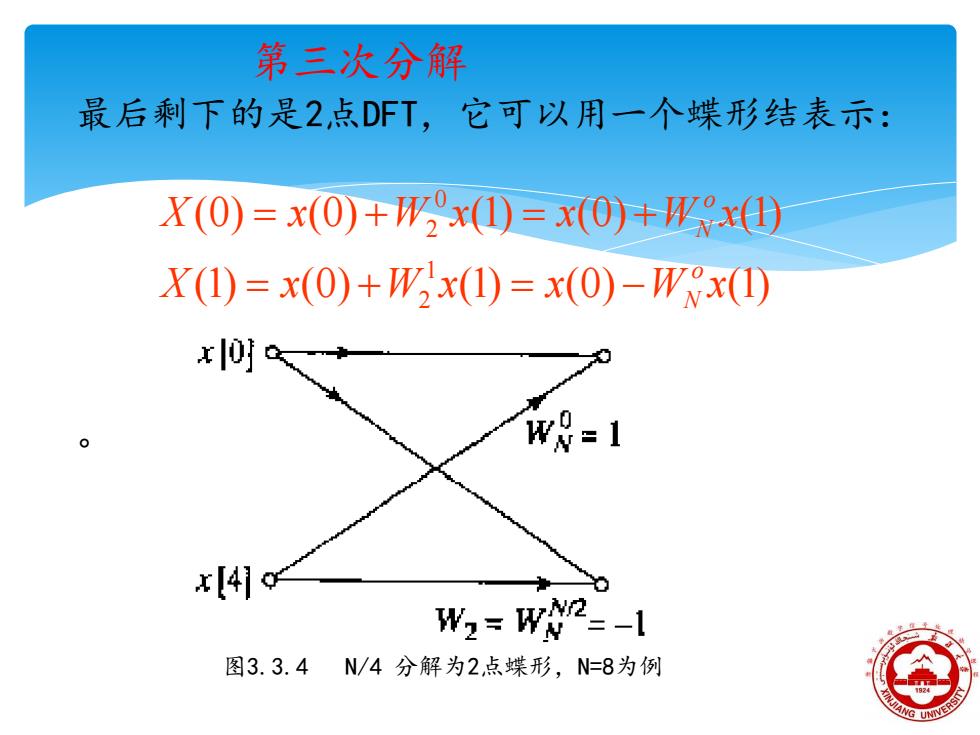
第三次分解 最后剩下的是2点DFT,它可以用一个蝶形结表示: X(0)=x(O)+W%x(I)=x(0)+Y9x) X(I)=x(0)+Wx(1)=x(0)-W9x(1 x0时 x[4] 0 W2=W2=-1 图3.3.4N/4分解为2点蝶形,N=8为例
最后剩下的是2点DFT,它可以用一个蝶形结表示: 。 (1) (0) (1) (0) (1) (0) (0) (1) (0) (1) 1 2 0 2 X x W x x W x X x W x x W x o N o N = + = − = + = + 第三次分解 图3.3.4 N/4 分解为2点蝶形,N=8为例

x(0)0 pX(0) N/4点 x(4)0 DFT pX(1) w N x(2)0+ pX(2) NW4点 x(6)0 DFT W 0 pX(3) -1W0 x(1)0* X(4) N/4点 x(5)0 DFT X(5) x(3)0 X(6) N/4点 x(7)0 DFT oX(7) 图3.3.5由四个2点DFT组成8,点DFT
N/4点 N/4点 N/4点 N/4点 图 3.3.5 由四个2点DFT组成8点DFT
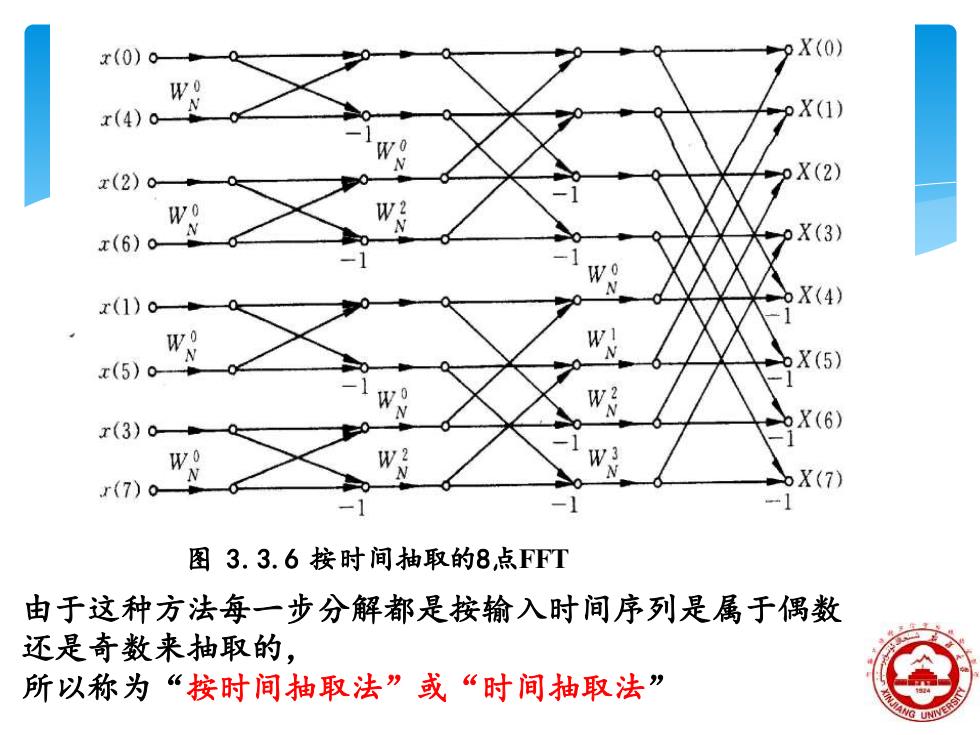
x(0) X(0) x(4)o pX(1) x(2)0 pX(2) W x(6)0 pX(3)》 x(1)0 6X(4) WX x(5)。 bX(5) x(3)0 X(6) w N N r(7)0 bX(7) 图3.3.6按时间抽取的8点F℉T 由于这种方法每一步分解都是按输入时间序列是属于偶数 还是奇数来抽取的, 所以称为“按时间抽取法”或“时间抽取法
图 3.3.6 按时间抽取的8点FFT 由于这种方法每一步分解都是按输入时间序列是属于偶数 还是奇数来抽取的, 所以称为“按时间抽取法”或“时间抽取法