
注意到,H(k),G(k)有N/2个点,即k=0,1,. N/2-1,还必须应用系数 W的周期性和对称性 表示X(k)的 N/2≈N-1点: 由 W12+k)三NN 3 得: 2 =W XW+之=6k)-m以k=0L义-1 W 2 2 可见,一个N,点的DFT被分解为两个N/2,点的DFT,这两个N/2 点的DFT再合成为一个N,点DFT
注意到,H(k),G(k)有N/2个点,即k=0,1, . , N/2-1,还必须应用系数 w k N 的周期性和对称性 表示 X(k)的 N/2 ~N-1点: 由 得: 可见,一个N点的DFT被分解为两个N/2点的DFT,这两个N/2 点的DFT再合成为一个N点DFT

风6=GG)+pH阳k0 xk+)=Gk)-m5H,k=01义-1 2 依此类推,G(k)和H(k)可以继续分下去,这种按时间 抽取算法是在输入序列分成越来越小的子序列上执行 DFT运算,最后再合成为W点的DFT
依此类推,G(k)和H(k)可以继续分下去,这种按时间 抽取算法是在输入序列分成越来越小的子序列上执行 DFT运算,最后再合成为N点的DFT
蝶形信号流图 将G()和H() 合成X()运算可归结为: a-bw a+bw a+bW a+bW a-bW a-bW (a) (6) 图3.3.1蝶形运算的简化 O UNINE
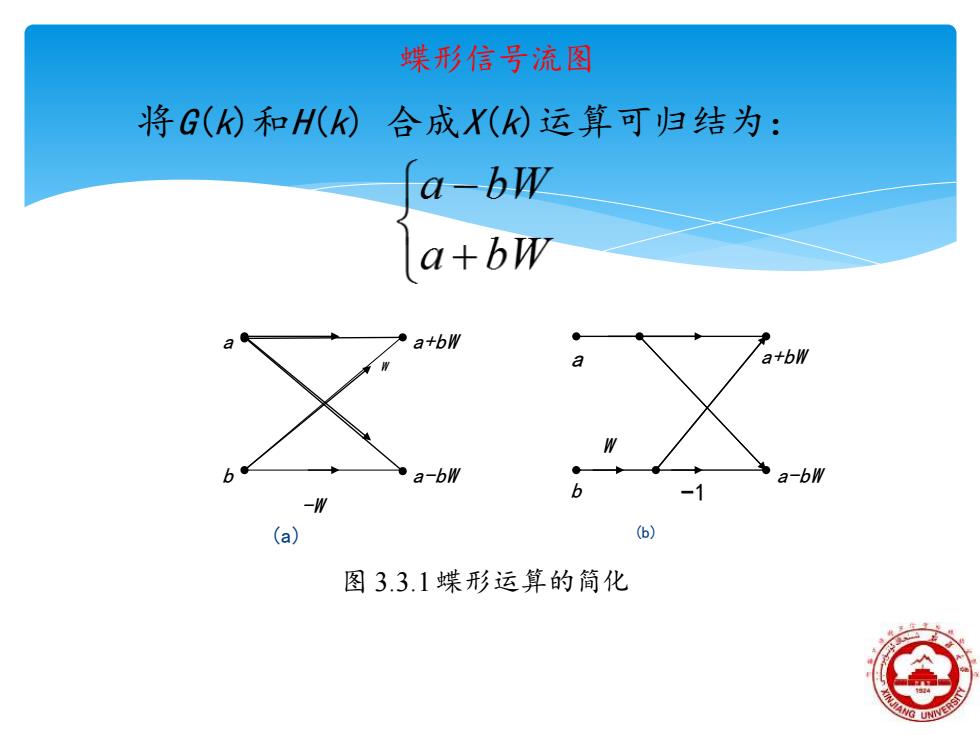
蝶形信号流图 将G(k)和H(k) 合成X(k)运算可归结为: W a+bW a-bW -W -1 a+bW a-bW W a b a b 图 3.3.1蝶形运算的简化 (a) (b)

蝶形运算 图(a)为实现这一运算的一般方法,它需要 两次乘法、两次加减法。考虑到-b和b俩个乘 法仅相差一负号,可将图(a)简化成图(b), 此时仅需一次乘法、两次加减法。图()的运 算结构像一蝴蝶通常称作蝶形运算结构简称蝶 形结,采用这种表示法,就可以将以上所讨论 的分解过程用流图表示
图 (a)为实现这一运算的一般方法,它需要 两次乘法、两次加减法。考虑到-bW和bW两个乘 法仅相差一负号,可将图 (a)简化成图 (b), 此时仅需一次乘法、两次加减法。图 (b)的运 算结构像一蝴蝶通常称作蝶形运算结构简称蝶 形结,采用这种表示法,就可以将以上所讨论 的分解过程用流图表示。 蝶形运算
流图表示:N=23=8的例子 第一次分解 x(O) G(0) X(0) x(2) N/2,点 G(1) X(1) x(4) DFT G(2) X(2) x(6) G(3) X3) x(1) H(O) WO X(4) x(3) N/2点 H(1) X5) x(5) DFT H2) R X6) x(7) H(3) X() 图3.3.2 两个4,点DFT组成8,点DFT
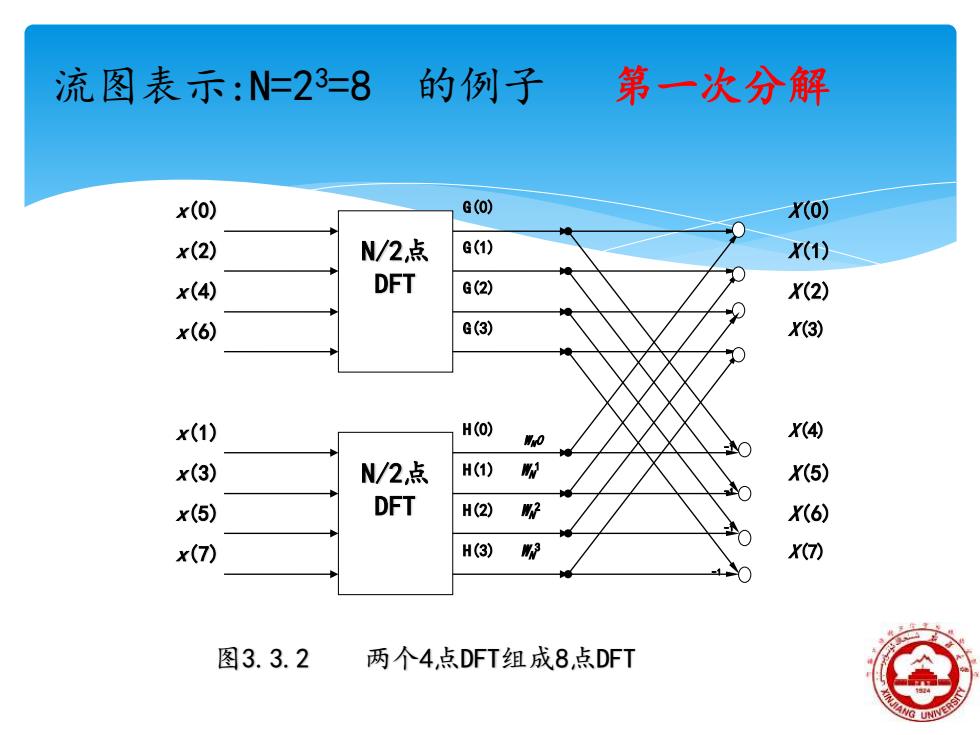
流图表示:N=2 3=8 的例子 第一次分解 N/2点 DFT G(0) G(1) G(2) G(3) X(0) X(1) X(2) X(3) x(0) x(2) x(4) x(6) N/2点 DFT H(0) H(1) H(2) H(3) X(4) X(5) X(6) X(7) x(1) x(3) x(5) x(7) WN 1 WN 2 WN 3 -1 -1 -1 -1 图3.3.2 两个4点DFT组成8点DFT WN0