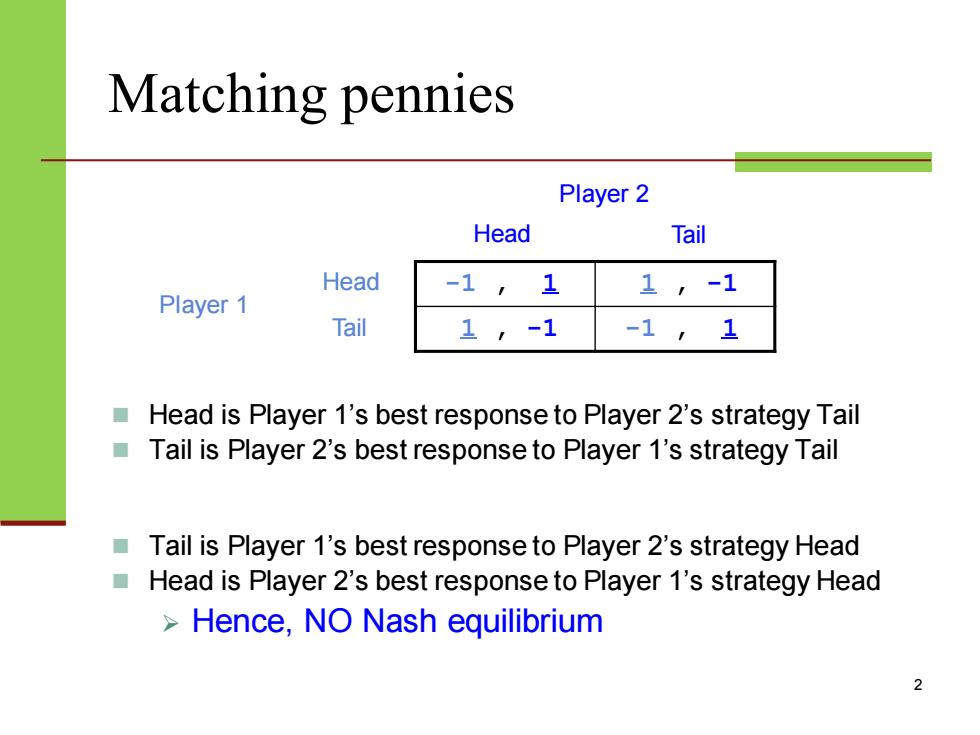
Matching pennies Player 2 Head Tail Head -1,1 1,-1 Player 1 Tail 1,-1 -1,1 Head is Player 1's best response to Player 2's strategy Tail Tail is Player 2's best response to Player 1's strategy Tail Tail is Player 1's best response to Player 2's strategy Head Head is Player 2's best response to Player 1's strategy Head Hence,NO Nash equilibrium 2
Matching pennies -1 , 1 1 , -1 1 , -1 -1 , 1 2 ◼ Head is Player 1’s best response to Player 2’s strategy Tail ◼ Tail is Player 2’s best response to Player 1’s strategy Tail ◼ Tail is Player 1’s best response to Player 2’s strategy Head ◼ Head is Player 2’s best response to Player 1’s strategy Head ➢ Hence, NO Nash equilibrium Player 1 Player 2 Tail Head Tail Head
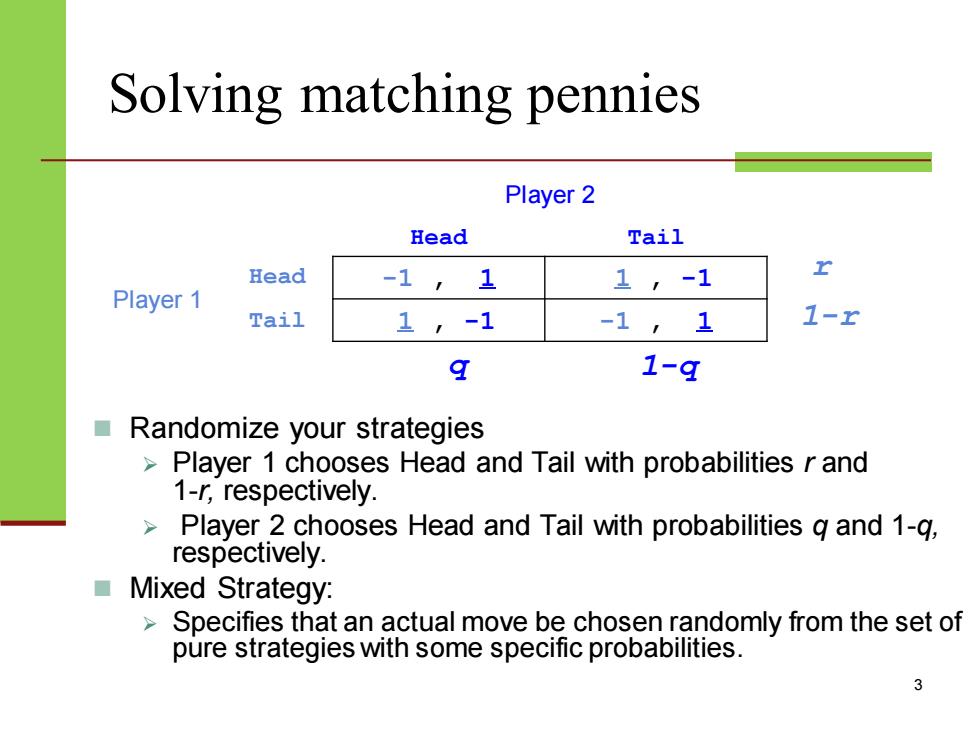
Solving matching pennies Player 2 Head Tail Head -1,1 1,-1 Player 1 Tail 1,-1 -1 ,1 1- 9 1-q ■ Randomize your strategies Player 1 chooses Head and Tail with probabilities r and 1-r,respectively. Player 2 chooses Head and Tail with probabilities g and 1-g, respectively. ■ Mixed Strategy: Specifies that an actual move be chosen randomly from the set of pure strategies with some specific probabilities. 3
Solving matching pennies Player 2 Head Tail Player 1 Head -1 , 1 1 , -1 Tail 1 , -1 -1 , 1 3 ◼ Randomize your strategies ➢ Player 1 chooses Head and Tail with probabilities r and 1-r, respectively. ➢ Player 2 chooses Head and Tail with probabilities q and 1-q, respectively. ◼ Mixed Strategy: ➢ Specifies that an actual move be chosen randomly from the set of pure strategies with some specific probabilities. q 1-q r 1-r

Mixed strategy ■ A mixed strategy of a player is a probability distribution over player's(pure)strategies. >A mixed strategy for Chris is a probability distribution(p,1-p), where p is the probability of playing Opera,and 1-p is that probability of playing Prize Fight. If p=1 then Chris actually plays Opera.If p=0 then Chris actually plays Prize Fight. Battle of sexes Pat Opera Prize Fight Opera (p) 2, 0, 0 Chris Prize Fight(1-p) 0,( 0 2 1
Mixed strategy Battle of sexes Pat Opera Prize Fight Chris Opera (p) 2 , 1 0 , 0 Prize Fight (1-p) 0 , 0 1 , 2 4 ◼ A mixed strategy of a player is a probability distribution over player’s (pure) strategies. ➢ A mixed strategy for Chris is a probability distribution (p, 1-p), where p is the probability of playing Opera, and 1-p is that probability of playing Prize Fight. ➢ If p=1 then Chris actually plays Opera. If p=0 then Chris actually plays Prize Fight
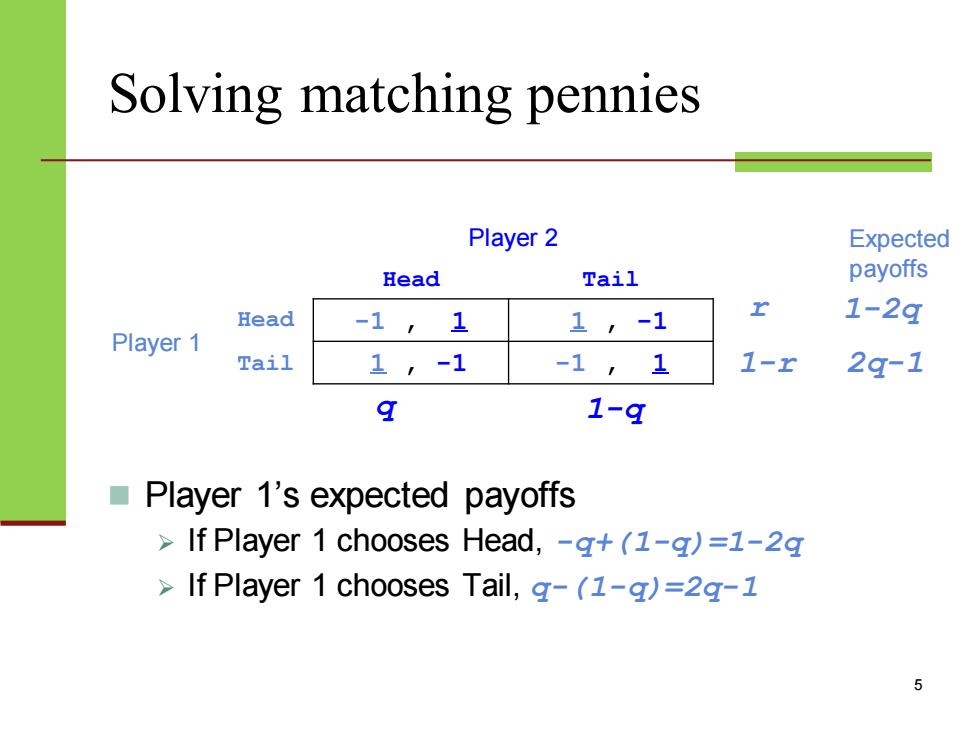
Solving matching pennies Player 2 Expected Head Tail payoffs Head -1 1 1,-1 r 1-2g Player 1 Tail 1,-1 -1, 1 1-r 2g-1 9 1-9 Player 1's expected payoffs If Player 1 chooses Head,-g+(1-g)=1-2g If Player 1 chooses Tail,g-(1-g)=2g-1
Solving matching pennies Player 2 Head Tail Player 1 Head -1 , 1 1 , -1 Tail 1 , -1 -1 , 1 5 ◼ Player 1’s expected payoffs ➢ If Player 1 chooses Head, -q+(1-q)=1-2q ➢ If Player 1 chooses Tail, q-(1-q)=2q-1 q 1-q 1-2q 2q-1 Expected payoffs r 1-r
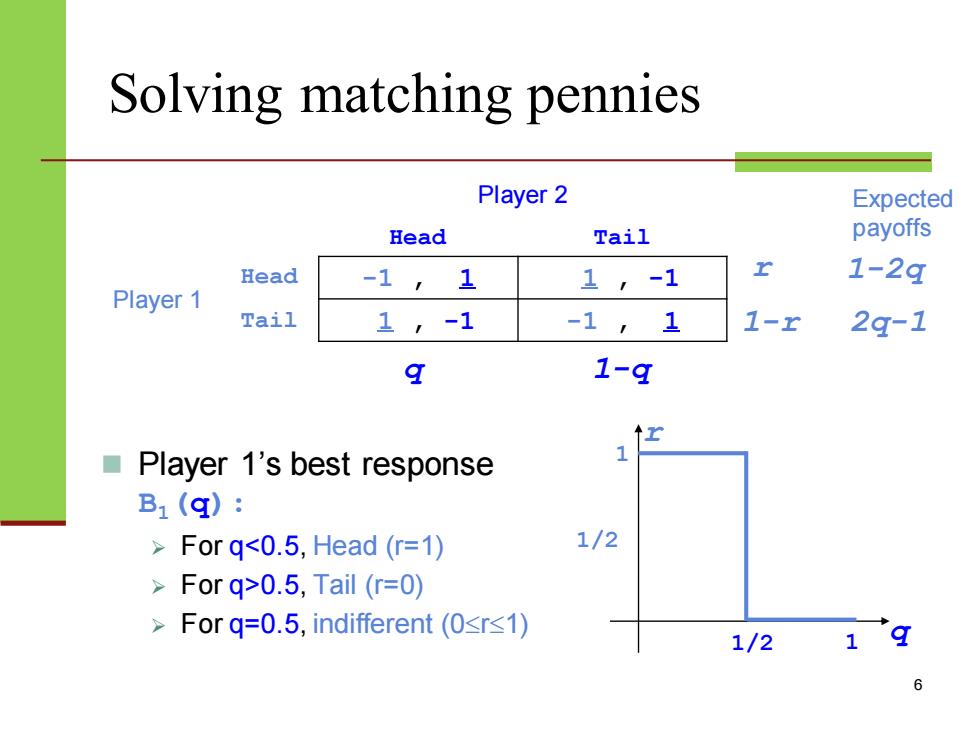
Solving matching pennies Player 2 Expected Head Tail payoffs Head -1, 1 1,-1 r 1-2q Player 1 Tail 1,-1 -1,1 1-r 2g-1 q 1-q ↑ Player 1's best response B1(g): For q<0.5,Head(r=1) 1/2 For q>0.5,Tail (r=0) For q=0.5,indifferent (0sr<1) 1/2 6
Solving matching pennies Player 2 Head Tail Player 1 Head -1 , 1 1 , -1 Tail 1 , -1 -1 , 1 6 ◼ Player 1’s best response B1(q): ➢ For q<0.5, Head (r=1) ➢ For q>0.5, Tail (r=0) ➢ For q=0.5, indifferent (0r1) 1 q r 1 1/2 1/2 q 1-q 1-2q 2q-1 Expected payoffs r 1-r