
9.1 Sampling Distributions Related to the Chapter 9 Sampling Distributions Xiaohan Yang Department of Mathematics,Tongji University 1口137,·百·至分0 Xiaohan Yang Chapter 9 Sampling Distributions
logo 9.1 Sampling Distributions Related to the Normal Distribution Sample Distribution Chapter 9 Sampling Distributions Xiaohan Yang Department of Mathematics, Tongji University Xiaohan Yang Chapter 9 Sampling Distributions

9.1 Sampling Distributions Related to the Normal Distributio Sample Distribution 1、X2 Distribution Let X1,...,Xn be a random sample of size n from a normal distribution with mean u and variance o2.Then i=N(0,1),i=1,...:n,and - has a x2 distribution with n degrees of freedom(df),denoted as rx2(n). 4口118,1三y2,至000 Xiaohan Yang Chapter 9 Sampling Distributions
logo 9.1 Sampling Distributions Related to the Normal Distribution Sample Distribution 1!χ 2 Distribution Let X1, · · · ,Xn be a random sample of size n from a normal distribution with mean µ and variance σ 2 . Then Zi = Xi −µ σ ∼ N(0, 1), i = 1, · · · , n, and Y = Xn i=1 Z 2 i has a χ 2 distribution with n degrees of freedom(df)§denoted as Y ∼ χ 2 (n). Xiaohan Yang Chapter 9 Sampling Distributions

9.1 Sampling Distributions Related to the Normal Distributio Sample Distribution the probability density function of x2 pdf of x Distribution 圣 1300100 Figure:the probability density function of x2 4口,48,5三。3分QC Xiaohan Yang Chapter 9 Sampling Distributions
logo 9.1 Sampling Distributions Related to the Normal Distribution Sample Distribution the probability density function of χ 2 0 2 4 6 8 0.0 0.2 0.4 0.6 0.8 1.0 1.2 pdf of χ 2 Distribution x f(x) n=1 n>1 Figure: the probability density function of χ 2 Xiaohan Yang Chapter 9 Sampling Distributions

9.1 Sampling Distributions Related to the Normal Distributio Sample Distribution Properties of x2 Distribution If y~x2(n),then E(Y)=n,D(Y)=2n Let X and Y independent,and X~x2(m),Y x2(n),then x+r x2(m+n) Ax2 distribution showing upper-tail area p-(n),can be found in Appendix table Example:Let (X1,...,X6)is a random sample from N(o,1),Y=(=1)2+(∑=4)2,find a number c such that the distribution of cy is x2 and find the degree of this distribution. 0a0 Xiaohan Yang Chapter 9 Sampling Distributions
logo 9.1 Sampling Distributions Related to the Normal Distribution Sample Distribution Properties of χ 2 Distribution 1 If Y ∼ χ 2 (n)§then E(Y ) = n, D(Y ) = 2n 2 Let X and Y independent§and X ∼ χ 2 (m), Y ∼ χ 2 (n)§then X + Y ∼ χ 2 (m + n) 3 A χ 2 distribution showing upper-tail area p))χ 2 p (n)§can be found in Appendix table 4 ExampleµLet (X1, · · · ,X6) is a random sample from N(0, 1)§Y = (P3 i=1 Xi) 2 + (P6 i=4 Xi) 2§find a number c such that the distribution of cY is χ 2 and find the degree of this distribution. Xiaohan Yang Chapter 9 Sampling Distributions
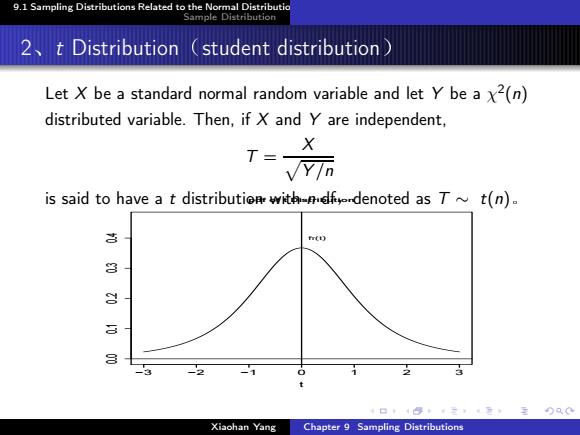
9.1 Sampling Distributions Related to the Normal Distributio Sample Distribution 2 t Distribution student distribution) Let X be a standard normal random variable and let Y be a x2(n) distributed variable.Then,if X and Y are independent, VN元 is said to have a t distribution with-ndf.denoted as Tt(n). 吉 8 Xiaohan Yang Chapter 9 Sampling Distributions
logo 9.1 Sampling Distributions Related to the Normal Distribution Sample Distribution 2!t Distribution£student distribution¤ Let X be a standard normal random variable and let Y be a χ 2 (n) distributed variable. Then, if X and Y are independent, T = X p Y /n is said to have a t distribution with n df§denoted as T ∼ t(n)" −3 −2 −1 0 1 2 3 0.0 0.1 0.2 0.3 0.4 pdf of t Distribution t fT(t) Figure: the probability density function of Xiaohan Yang Chapter 9 Sampling Distributions t distribution