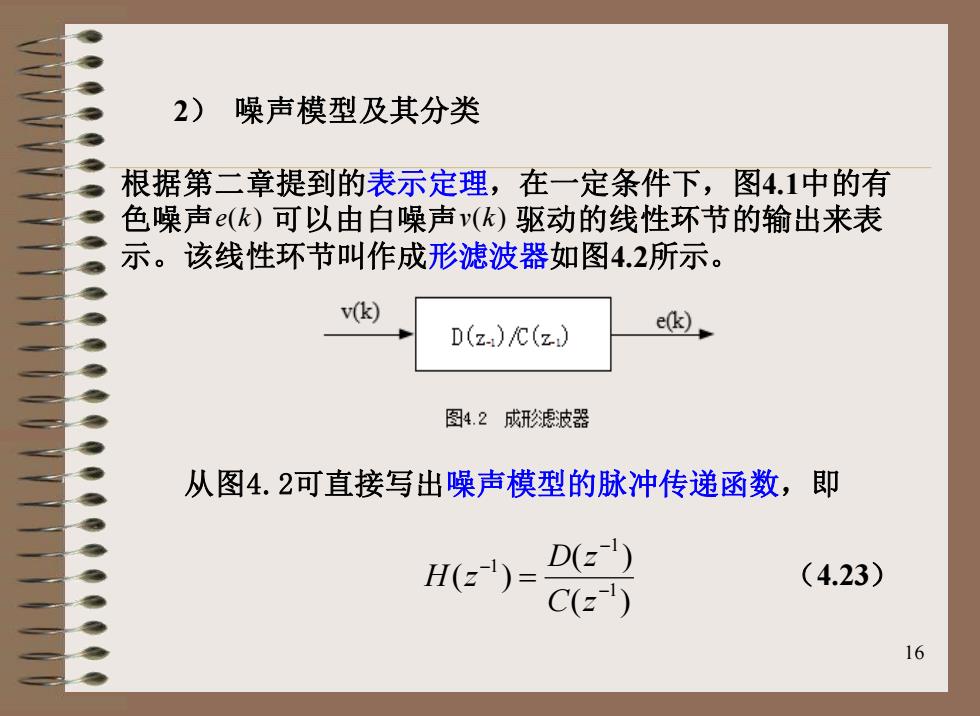
2) 噪声模型及其分类 根据第二章提到的表示定理,在一定条件下,图4.1中的有 色噪声(k)可以由白噪声v(k)驱动的线性环节的输出来表 示。该线性环节叫作成形滤波器如图4.2所示。 v(k) D(z.)/C(z) e(k), 图4.2成形滤波器 从图4.2可直接写出噪声模型的脉冲传递函数,即 He)=Ce可 D(=) (4.23) 16
16 2) 噪声模型及其分类 根据第二章提到的表示定理,在一定条件下,图4.1中的有 色噪声 可以由白噪声 驱动的线性环节的输出来表 示。该线性环节叫作成形滤波器如图4.2所示。 ( ) ( ) ( ) 1 1 1 − − − = C z D z H z 从图4.2可直接写出噪声模型的脉冲传递函数,即 (4.23) e(k) v(k)

v(k)是白噪声,噪声模型(4.23)式直接决定(k)的噪声 特点。在上式中,如果C(马或Dz简化为1,则噪声模型 的结构和特性也随之改变。根据其结构,噪声模型可分为 以下三种类型: ①自回归模型, 简称AR模型,其模型结构为 (4.24) C(ze(k)=v(k) ② 平均滑动模型,简称MA模型,其模型结构为 e(k)=D(z)v(k) (4.25) ③ 自回归平均滑动模型,简称ARMA模型,其模型结构为 C(ze(k)=D(z)v(k) (4.26) 17
1717 v(k) 是白噪声,噪声模型(4.23)式直接决定 的噪声 特点。在上式中,如果 或 简化为1,则噪声模型 的结构和特性也随之改变。根据其结构,噪声模型可分为 以下三种类型: ① 自回归模型,简称AR模型,其模型结构为 ② 平均滑动模型,简称MA模型,其模型结构为 ③ 自回归平均滑动模型,简称ARMA模型,其模型结构为 (4.26) ( ) ( ) ( ) 1 C z e k = v k − ( ) ( ) ( ) 1 e k D z v k − = ( ) ( ) ( ) ( ) 1 1 C z e k D z v k − − = e(k) ( ) −1 C z ( ) −1 D z (4.25) (4.24)

4.3.2极大似然估计与最小二乘估计的关系 将模型(4.21)式写成 z1=H0+e (4.27) 其中 21=[z(1),z(2),…,z(L] ez=[e(),e(2),…,e(L] 8=[a1a2,…,an,b,b2,…,bn] -z(0) -z1-n) u(0) … u(1-n) -z(1) -z(2-n) u() u(2-n) HL= 。… (L-) …-z(L-n) u(L-1) u(L-n) (4.28) 18
18 4.3.2 极大似然估计与最小二乘估计的关系 将模型(4.21)式写成 L HL eL (4.27) z = + 其中 − − − − − − − − − − − − − − = = = = ( 1) ( ) ( 1) ( ) (1) (2 ) (1) (2 ) (0) (1 ) (0) (1 ) [ , , , , , , ] [ (1), (2), , ( )] [ (1), (2), , ( )] 1, 2 1 2 z L z L n u L u L n z z n u u n z z n u u n H a a a b b b e e e e L z z z z L L n n L L (4.28)

因为e(k)=v(k)+dv(k-1)+…+dn(k-n) (4.29) 则有 E{e(k)e(k-}=∑d,d-,o dA1;d=0l<0或1>m) (4.30) 噪声e(k)的协方差阵记作 Efe(1)e(1); E{e(I)e(2)} … Efe(1)e(L); E{e(2)e(I)} E{e(2)e(2)} ∑e=E{eei} E{e(2)e(L)} (4.31) Efe(L)e(1); E{e(L)e(2)} …E{e(L)e(L)} 由于噪声服从正态分布,系统的输出测量也服从正态 分布,即 ~V(H0,Σe) (4.32) 19
1919 因为 ( ) ( ) ( 1) ( ) e k = v k + d1 v k − ++ dn v k − n (4.29) 则有 = − = = − 1; 0( 0 或 ) { ( ) ( )} 0 0 2 d d l l n E e k e k j d d l n l l l j v (4.30) 噪声 e(k) 的协方差阵记作 = = e L L E e L e E e L e E e L e L E e e E e e E e e L E e e E e e E e e L E e e { ( ) (1)} { ( ) (2)} { ( ) ( )} { (2) (1)} { (2) (2)} { (2) ( )} { (1) (1)} { (1) (2)} { (1) ( )} { } (4.31) 由于噪声服从正态分布,系统的输出测量也服从正态 分布,即 ~ ( , ) L HL e z N (4.32)

根据统计,正态分布的随机变量x的概率密度表达式为 1 (x-x)2 (4.33) 式中,X为正态分布函数中心值,0 为尺度因子。则在参 数日条件下,2L的概率密度函数可以写成 p-.0)-(2z)(detE.)iexp-i(-.-H.0Yz.G--H.0) (4.34) 据此,对数似然函数可以写成 I(z10)=In L(z1e)=In p(=10) =-h2r-2hdet2,e-H0jz长-H.0)4.36) 根据极大似然原理,将(4.35)式对日求导并令其等于零, 可得 0=(H2。H)H2。'L (4.36)20
20 根据统计,正态分布的随机变量x的概率密度表达式为 − = − 2 2 ( ) exp 2 1 ( ) x x p x (4.33) 式中, x 为正态分布函数中心值, 为尺度因子。则在参 数 条件下, 的概率密度函数可以写成 2 L z ( ) ( ) ( ) ( ) = − − − − − − e L L e L L L p zL z H z H 1 2 1 2 2 1 ( ) 2 det exp (4.34) 据此,对数似然函数可以写成 ( ) ln ( ) ln ( ) L L L l z = L z = p z ( ) ( ) e L L e L HL z H z L = − − − − − −1 2 1 ln det 2 1 ln 2 2 (4.35) 根据极大似然原理,将(4.35)式对 求导并令其等于零, 可得 ML L e L L e L H H H z 1 1 1 ( ) ˆ − − − = (4.36)