
oo p(=l0 (4.14) 综合考虑故(4.10)和(4.14)式,有1(0,0)≥0 (4.15) 式(4.5)要求p(z0)取极大值,这就意味着I(0,θ)必须取极 小值。根据I(旧,0)的定义,并考虑到对一个给定的随机变 量Z,其概率密度函数p(z旧o)是确定的,显然,从(4.10) 式可知,极小化IO,8)等价于极大化Elnp(O)},由于 Elnp(ce)}与L(3,IO)之间存在单调的函数关系,所以极 大化L(20)或lnL(2,O)与极大化E{Inp(=10)}是等效的。 因此(4.3)或(4.4)式体现了极大似然原理的内在实质,它们 是极大似然辨识的重要依据。 进入例题4.1
进入例题4.1 11 0 | ln 0 | p z E p z (4.14) 综合考虑故(4.10)和(4.14)式,有 (4.15) 0 I( , ) 0 式(4.5)要求 取极大值,这就意味着 必须取极 小值。根据 的定义,并考虑到对一个给定的随机变 量Z,其概率密度函数 是确定的,显然,从(4.10) 式可知,极小化 等价于极大化 ,由于 与 之间存在单调的函数关系,所以极 大化 或 与极大化 是等效的。 因此(4.3)或(4.4)式体现了极大似然原理的内在实质,它们 是极大似然辨识的重要依据。 p z( | ) 0 I( , ) 0 I( , ) 0 ( | ) L p z 0 I( , ) E p z {ln ( | )} E p z {ln ( | )} ( | ) L L z ( | ) L L z ln ( | ) L L z E p z {ln ( | )}

例4.1考虑一个独立同分布的随机过程{x()},在参数0条 件下随机变量x的概率密度为p(x0)=02xe8x,0>0,试用 解析法求参数日的极大似然估计。 解:设x,=[x(),x(2),…,xL)]严表示随机变量x的L个观测值 的向量,那么随机变量x在参数条件下的似然函数为 ,o)-直p(eW1o=62L直exp-B管W] (4.16) 对应的对数似然函数为 ,o=h,=2n6+含nM)-0容 (4.17) 12
12 例 4.1 考虑一个独立同分布的随机过程 ,在参数 条 件下随机变量x的概率密度为 ,试用 解析法求参数 的极大似然估计。 { ( )} x t p x xe ( | ) , 0 = 2 −x 解:设 表示随机变量x的L个观测值 的向量,那么随机变量x在参数 条件下的似然函数为 [ (1), (2), , ( )] L x x x x L = 1 1 1 ( | ) ( ( )| ) ( )exp[ ( )] 2 L L L L k k k L x p z k x k x k L = = = = = − (4.16) 对应的对数似然函数为 1 1 ( | ) ln ( ) 2 ln ln ( ) ( ) L L L L k k l x L x L x k x k = = = = + − (4.17)

根据(4.4)式,则有 al(x,le) =2L1- a0 -0 (4.18) 从而可得 6u=2管x内 (4.19) 又由于 2InL(x,l0) =- o02 2L<0 (4.20) 所以8M使似然函数达到了最大值。因此9M是参数θ 的极大似然估计值。 13
13 根据(4.4)式,则有 1 ( | ) 1 2 ( ) 0 ˆ ˆ L L k ML ML l x L x k = = − = (4.18) 从而可得 1 ˆ 2 ( ) L ML k L x k = = (4.19) 又由于 2 2 2 ln ( | ) 2 0 ˆ ˆ L ML ML L x L =− (4.20) 所以 使似然函数达到了最大值。因此 是参数 的极大似然估计值。 ˆ ML ˆ ML
4.3动态系统模型参数的极大似然估计 4.3.1动态模型描述 1)动态系统模型 动态模型示意图如图4.1所示。设: A(z-I)=C(z-I),e()=v(k)/C(z-),则有 D (K) C(z-) e(k) B(-1) 2(k) u(k) A(2I) 图4.1动态模型示意图 14
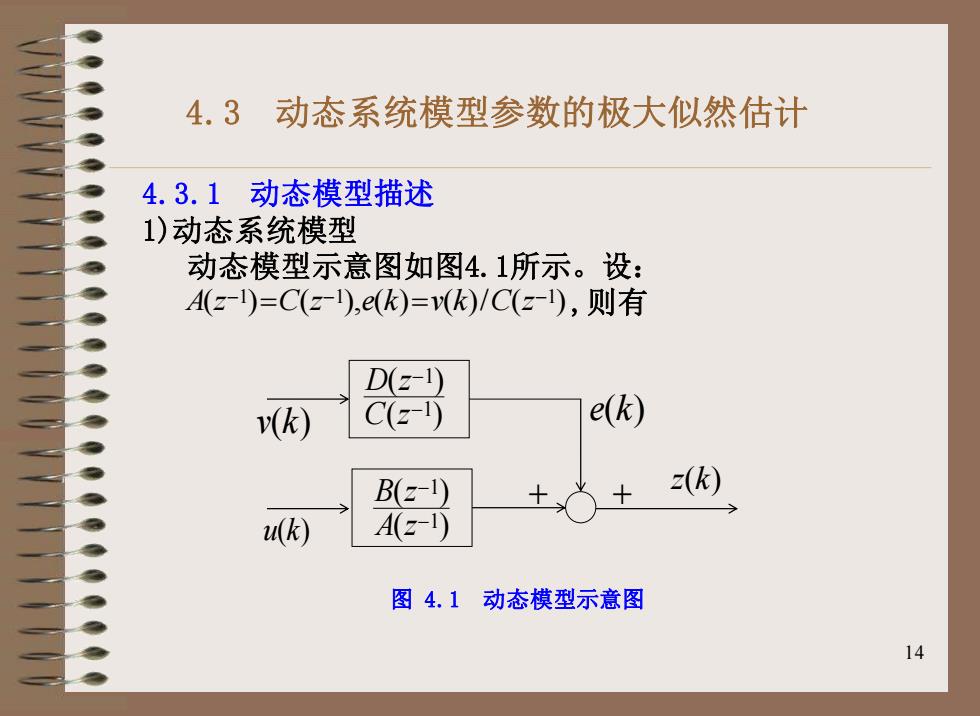
14 4.3 动态系统模型参数的极大似然估计 4.3.1 动态模型描述 1)动态系统模型 动态模型示意图如图4.1所示。设: A z C z e k v k C z ( ) ( ), ( ) ( )/ ( ) − − − 1 1 1 = = ,则有 1 1 ( ) ( ) D z C z − − 1 1 ( ) ( ) B z A z − − v k( ) u k( ) + + z k( ) e k( ) 图 4.1 动态模型示意图

A(2-1)z(k)=B(z-1u(k)+e(k) e(k)=D(z-1)v(k) (4.21) 其中,v(化是均值为零,方差为如?,服从正态分布的不 相关随机噪声;()和z(k)表示系统的输入输出变量;且 A(2-)=l+a2-l+a22-2++an2-n B(2-1)=bz-1+b,2-2++bn2n (4.22) D(z-)=l+dz-1+d22++dn2-m 同时,设系统稳定,即A(z)和D(z)的所有零点都位于 z平面的单位圆内,且4(z-)、B(z)和D(z)没有公共因 子,这意味过程是渐进稳定的。 15
15 1 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) A z z k B z u k e k e k D z v k − − − = + = (4.21) 其中, 是均值为零,方差为 ,服从正态分布的不 相关随机噪声; 和 表示系统的输入输出变量;且 v k( ) 2 v u k( ) z k( ) 1 1 2 1 2 1 1 2 1 2 1 1 2 1 2 ( ) 1 ( ) ( ) 1 n n n n n n A z a z a z a z B z b z b z b z D z d z d z d z − − − − − − − − − − − − = + + + + = + + + = + + + + (4.22) 同时,设系统稳定,即 和 的所有零点都位于 z平面的单位圆内,且 、 和 没有公共因 子,这意味过程是渐进稳定的。 1 A z( ) − 1 D z( ) − 1 A z( ) − 1 B z( ) − 1 D z( ) −