
x为未反应单体中M的重量分率 K为MM,代表两单体的相对分子质量之比 类似地也可以表示为以重量比或重量分率表示的共聚组成微分方程。在不同的场合,可 根据具体情况选用不同的方程。 归纳起来,在以动力学方法推导共聚物组成议程时曾作了下面几个假定: ①不考虑解聚反应,设聚合反应为正向的不可逆反应: ②不考虑前末端效应,链自由基一端倒数第二个单元对自由基活性无影响: ③等活性假定,自由基活性与链长无关: ④聚合度很大,引发和终止反应对共聚物组成没有影响: ⑤稳态假定,体系中自由基总浓度和两种自由基的浓度都不变,即要求引发速率和 终止速率相等,同时两种自由基相互转化的速度相等。 对于多数自由基二元共聚而言,上述假定均可成立。一些超出此范围的情况将在后面给 予讨论。对于离子型二元共聚,在多数情况下上述公式依然成立。 7.2.2共聚物组成曲线 式7一11反映了共聚反应某一瞬间所形成共聚物的组成与这一瞬间体系单体组成之间关 系。可以看出影响共聚组成的主要因素是两种单体浓度及它们的竞聚率。 在二元共聚反应中,活性中心~~M·可同时与两种不同的单体反应,即有在一对相互 竞争的链增长反应: M1→MM1· ~一M1·+ M→一MM· 对单体M的竞聚率定义为:互=L,标征~M·链自由基同自身单体M进行自聚的反 k 应能力与同异种单体M进行共聚的反应能力之比。反过来看,也就是两种单体与同一种链 自由基反应的相对活性。从单体的角度看,竞聚率反映了竞争聚合时两种单体反应活性的比 较:从聚合的角度看,竞聚率反映了链自由基进行自聚与共聚的能力比较。因此竞聚率是判 断单体活性和共聚行为的重要参数。 当n>1,即k>k12时,表明链自由基~~M·易和自身单体M反应而不易和异种 单体M反应。易自聚而不易共聚,或均聚倾向大于共聚倾向。 当n<1,即k1<k2时,表明链自由基~~M·易和异种单体M反应而不易和自身 单体M反应。易共聚而不易自聚,或共聚倾向大于自聚倾向。 当=1,即k1=k2时,表明链自由基~M·和两种单体M、M反应的活性相同 发生均聚和发生共聚的几率相等。 当1=0,即k1=0,k2≠0时,表明链自由基~~M·只能和异种单体M反应而不能 和自身单体M,反应。即只能共聚而不能自聚。 当r,=∞,即k11≠0,k2≈0时,表明链自由基一一M·只能和同种单体M1反应而不 能和异种单体M反应,即只能自聚而不能共聚。在实际中尚未发现这种情祝。 对:也可进行类似的分析。 式7-14表明共聚组成F是单体组成的函数。当竞聚率确定后,对于一系列不同的单 6
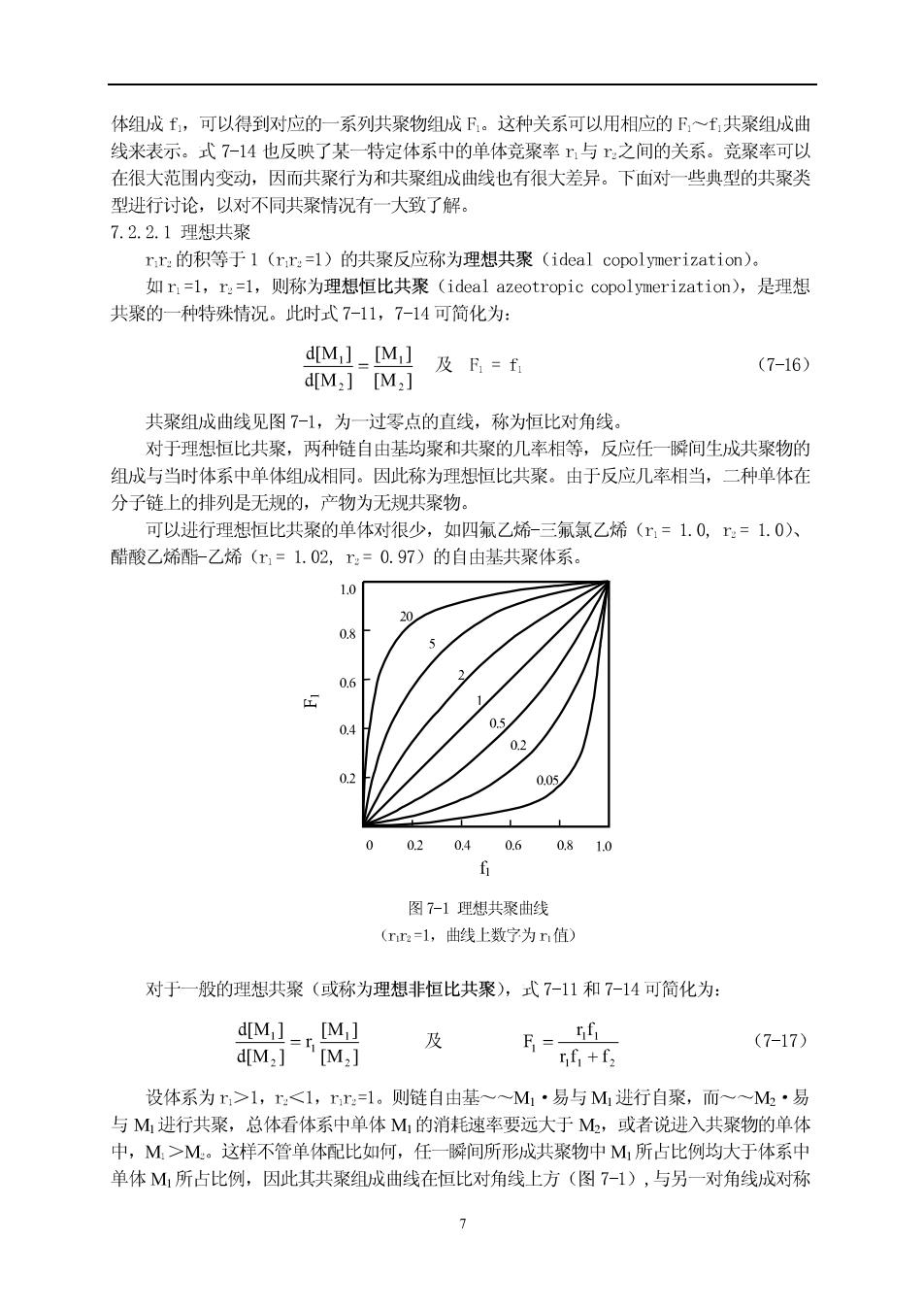
体组成f,可以得到对应的一系列共聚物组成F。这种关系可以用相应的F~共聚组成曲 线来表示。式7-14也反映了某一特定体系中的单体竞聚率与之间的关系。竞聚率可以 在很大范制内变动,因而共聚行为和共聚组成曲线也有很大差异。下由对一些典型的共聚类 型进行讨论,以对不同共聚情况有一大致了解。 7.2.2.1理想共聚 rr:的积等于1(rr=l)的共聚反应称为理想共聚(ideal copolymerization)。 如r=l,r=l,则称为理想恒比共聚(ideal azeotropic copolymerization),是理想 共聚的一种特殊情况。此时式7-11,7-14可简化为: dM1-M及B=E (7-16) dM2][M,】 共聚组成曲线见图7-1,为一过零点的直线,称为恒比对角线。 对于理想恒比共聚,两种链自由基均聚和共聚的几率相等,反应任一瞬间生成共聚物的 组成与当时体系中单体组成相同。因此称为理想恒比共聚。由于反应几率相当,二种单体在 分子链上的排列是无规的,产物为无规共聚物。 可以进行理想恒比共聚的单体对很少,如四氟乙烯-三氟氯乙烯(=1.0,r=1.0)、 醋酸乙烯酯乙烯(x=1.02,x=0.97)的自由基共聚体系。 1.0 05 0 0204 0.6081.0 图7-1理想共聚曲线 (rr2=l,曲线上数宁为r,值】 对于一般的理想共聚(或称为理想非恒比共聚),式7-11和7-14可简化为: 及 E,+ t (7-17) 设体系为>1,r<1,r=1。则链自由基~~M1·易与M进行自聚,而~~M·易 与M进行共聚,总体看体系中单体M,的消耗速率要远大于M,或者说进入共聚物的单体 中,M>M。这样不管单体配比如何,任一瞬间所形成共聚物中M所占比例均大于体系中 单体M所占比例,因此其共求组成曲线在恒比对角线上方(图7-1),与另一对角线设对际 7

状况,且r值越大,共聚组成曲线距恒比对角线越远。对<1,>1,r,=1的体系,可 作相同的分析,不过这时的共聚组成曲线在恒比对角线的下方(图7-1) 理想共聚概念的提出借用了理想液体混合物中的气液平衡特性,并不是说这类共聚反应 在任何意义上都是最理想的。理想共聚的一个极其重要、具有实际意义的结论是随着两种单 体竞聚率差别的增大,要合成两种单体含量都较高的共聚物就越困难。在:=1的条件下: KiK2L (7-18 k12 k22 说明两种单体结合到共聚物上的相对速率与链自由基种类无关,为无规共聚,共聚物中两单 体单元摩尔比是体系中两单体摩尔比的,倍。当两单体的竞聚率相差过大时,就得不到含有 大量单体M的共聚物。如=10,n0.1,即使投料时M的摩尔含量为80%,所得共聚物 中M的单元结构的摩尔含量仅为18.5%。只有当和r:没有显著差别时(如r0.5~2), 才会在很大的共聚单体投料组成的范围内得到两种单体含量都较多的共聚物。 60℃时丁二烯(m=1.39)-苯乙烯(=0.78)、偏二氯乙烯(=3.2)-氯乙烯 (=0.3)的自由基共聚体系接近理想共聚。大多数离子型共聚(包括阳离子共聚和阴离子 共聚),具有理想共聚的特征。 7.2.2.2交替共聚 交替共聚的典型特征为rr=0 对于两种单休的竞聚率均为零或均趋于零的体系,两种链自由基都不能和自身单体进行 均聚而只能与异种单体进行共聚,所形成共聚中两种单体单元严格交替排列。不论单体投 单体投料配比如何,当含量少的单体消耗光后聚合反应不再进行,剩下末反应的含量多的单 体,即共聚组成与单体组成、转化率无关。 式7-11和7-14可简化为: (7-19) 共聚组成曲线见图7-2,为一条水平线。 能够进行自由基交替共聚的体系不多,如马米酸酐和乙酸2氯烯丙基酯、异丁烯和反丁 烯二酯二乙酯。离子型共聚由于取代基极性效应的影响,交替共聚的倾向要比自由基共聚小 如m>0,=0,则式7-11为 瑞1 (7-20) 单体M的一定的自聚能力,M则只能共聚而不能均聚。当较小、M过量较多时,产物 基本为交替共聚物。如两种单体的活性相差不多,则共聚物中F>50%。60℃苯乙烯(r=0.01) 和马来酸酐(=0)自由基共聚就是这方面的例子
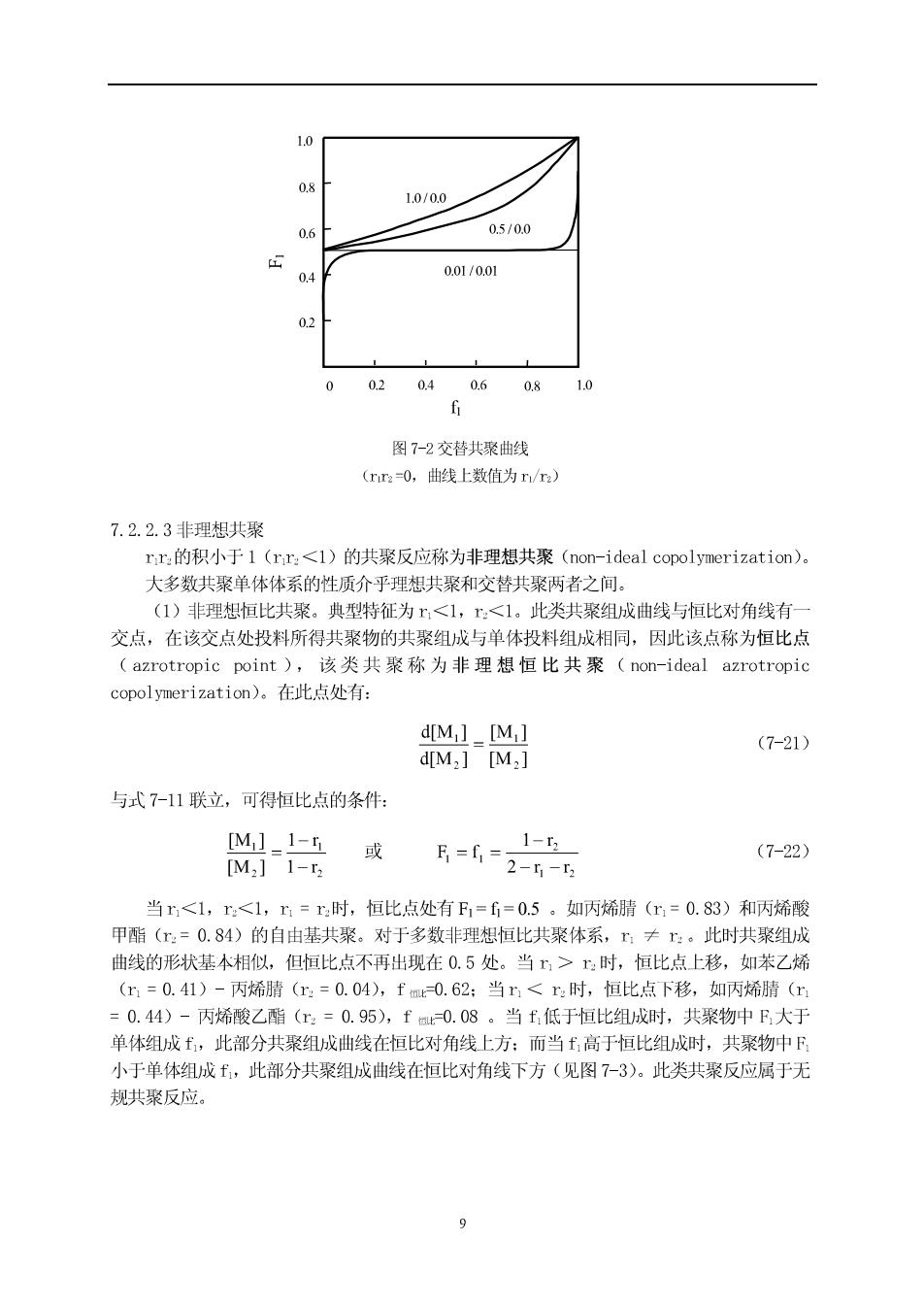
1.0/00 0510.0 0.01/0.01 02 04 0.6 0.8 图7-2交替共聚曲线 (nn-0,曲线上数值为n/m) 7.2.2.3非理想共聚 rr的积小于1(rr:<1)的共聚反应称为非理想共聚(nor-ideal copolymerization): 大多数共聚单体体系的性质介乎理想共聚和咬替共聚两者之间。 (1)非理想恒比共聚。典型特征为<1,1:<1。此类共聚组成曲线与恒比对角线有一 交点,在该交点处投料所得共聚物的共聚组成与单体投料组成相同,因此该点称为恒比点 (azrotropic point),该类共聚称为非理想恒比共聚(non-ideal azrotropic copolymerization),在此点处有: d[M,][M (7-21) dM2][M,] 与式7-11联立,可得恒比点的条件: [M]_1- [M,]1-2 或 E=i=2-- 1-2 (7-22) 当r<1,<1,=时,恒比点处有F1=6=0.5。如丙烯腈(m=0.83)和丙烯酸 甲酯(r:=0.84)的自由基共聚。对于多数非理想恒比共聚体系,r≠r:。此时共聚组成 曲线的形状基本相似,但恒比点不再出现在0.5处。当>时,恒比点上移,如苯乙烯 (11=0.41)-丙烯腈(12=0.04),fm0.62:当r<时,恒比点下移,如丙烯腈(r =0.44)-丙烯酸乙酯(:=0.95),fa0.08。当低于恒比组成时,共聚物中B大于 单体组成,此部分共聚组成曲线在恒比对角线上方:而当高于恒比组成时,共聚物中F 小于单体组成,此部分共聚组成曲线在恒比对角线下方(见图7-3)。此类共聚反应属于无 规共聚反应
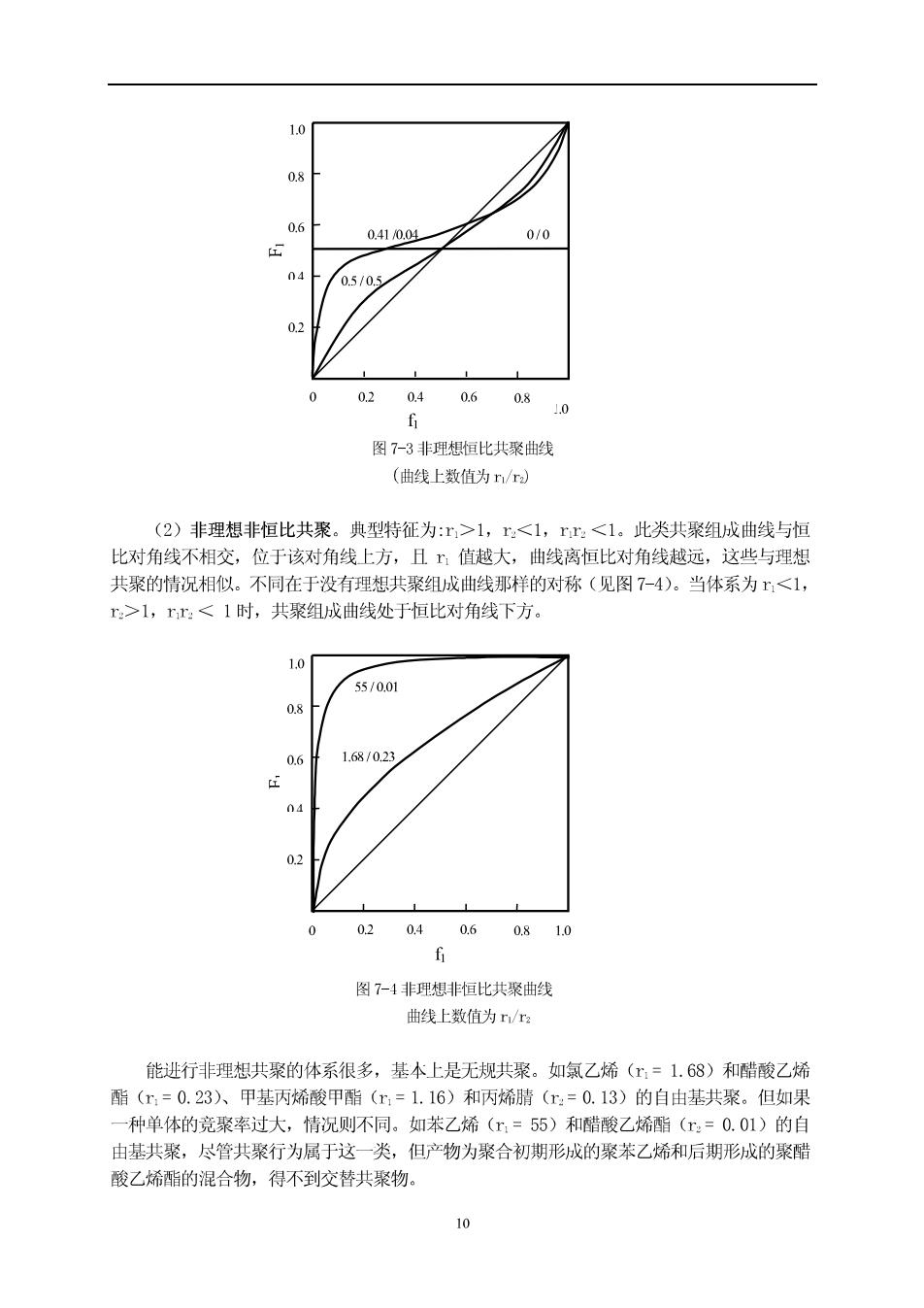
0.41004 0/0 0 0.5/0s 02 040.608 1.0 f 图7-3非理想恒比共聚曲线 (曲线上数值为r/r) (2)非理想非恒比共聚。典型特征为:r>1,<1,rr<1。此类共聚组成曲线与恒 比对角线不相交,位于该对角线上方,且?值越大,曲线离恒比对角线越远,这些与理想 共聚的情况相似。不同在于没有理想共聚组成曲线那样的对称(见图7-4)。当体系为工<1, r>1,rr<1时,共聚组成曲线处于恒比对角线下方。 1.01 55/001 1.68/023 0 0204 0.6 0.810 6 图?-4非理想非恒比共聚曲线 曲线上数值为n/ 能进行非理想共聚的体系很多,基本上是无规共聚。如氯乙烯(=1.68)和醋酸乙烯 酯(m=0.23)入、甲基丙烯酸甲酯(m=1.16)和丙烯腈(r:=0.13)的自由基共聚。但如果 一种单体的竟聚率过大,情况则不同。如苯乙烯(m=55)和醋酸乙烯酯(x=0.01)的自 由基共聚,尽管共聚行为属于这一类,但产物为聚合初期形成的聚苯乙烯和后期形成的聚醋 酸乙烯酯的混合物,得不到交替共聚物