
电子科越女学 r街y时Bectrele8 cad Tecaology af Chiaa /956 本次课内容 一、完全图、偶图与补图 二、顶点的度与图的度序列
本次课内容 一、完全图、偶图与补图 二、顶点的度与图的度序列

电子科越女学 r街y时Bectrele8 ciad Tecaology af Chins /956 一、完全图、偶图与补图 (一)、完全图 1、在图论中,完全图是一个简单图,且任意一个 顶点都与其它每个顶点有且只有一条边相连接。 2、n个顶点的完全图用K表示,常称为n阶完全图。 1阶完全图K, 2阶完全图K2 3阶完全图K3 5阶完全图K 注:有人认为符号来源于Kuratowski图论
一、完全图、偶图与补图 (一)、完全图 1、在图论中,完全图是一个简单图,且任意一个 顶点都与其它每个顶点有且只有一条边相连接。 2、n个顶点的完全图用Kn表示,常称为n阶完全图。 1阶完全图K1 2阶完全图K2 3阶完全图K3 5阶完全图K5 注:有人认为符号来源于Kuratowski图论

电↓科越女学 r街y时Bectrele8 cad Tecaology af Chiaa /956 很明显,K的边数为: m(K)=5n(n-1) 完全图在图论中是一个很基本的图,经常用到。 (二)、偶图(双图或者二部图) 1、一个实例 例1学校有6位教师将开设6门课程。六位教师的代号是 x(i=1,2,3,4,5,6),六门课程代号是y1(i=1,2,3,4,5,6)。已知, 教师x1能够胜任课程y2和y3;教师x2能够胜任课程y4和ys: 教师x3能够胜任课程y2;教师x4能够胜任课程y和y3; 教师x能够胜任课程y1和y6;教师x,能够胜任课程ys和y6 请画出老师和课程之间的状态图
很明显,Kn的边数为: 1 ( ) ( 1) 2 mK nn n 完全图在图论中是一个很基本的图,经常用到。 (二)、偶图(双图或者二部图) 1、一个实例 例1 学校有6位教师将开设6门课程。六位教师的代号是 xi(i=1,2,3,4,5,6),六门课程代号是yi (i=1,2,3,4,5,6)。已知, 教师x1能够胜任课程y2和y3;教师x2能够胜任课程y4和y5; 教师x3能够胜任课程y2;教师x4能够胜任课程y6和y3; 教师x5能够胜任课程y1和y6;教师x6能够胜任课程y5和y6。 请画出老师和课程之间的状态图
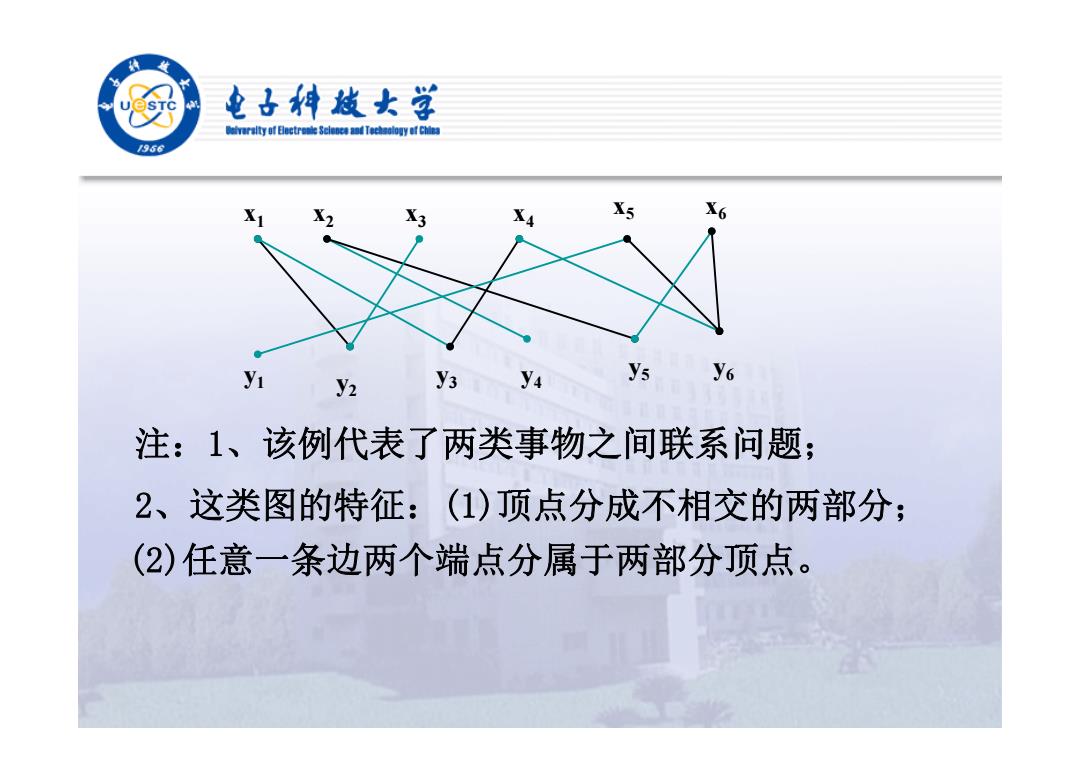
电子科越女学 r街y时Bectrele8 ciad Tecaology af Chins /956 X X3 X4 X5 X6 y1 y3 y4 ys y6 y2 注:1、该例代表了两类事物之间联系问题; 2、这类图的特征:(1)顶点分成不相交的两部分; (2)任意一条边两个端点分属于两部分顶点
注:1、该例代表了两类事物之间联系问题; x 1 x x 5 x 2 x 3 4 x 6 y 1 y y 3 y 4 2 y 5 y 6 2、这类图的特征:(1)顶点分成不相交的两部分; (2)任意一条边两个端点分属于两部分顶点
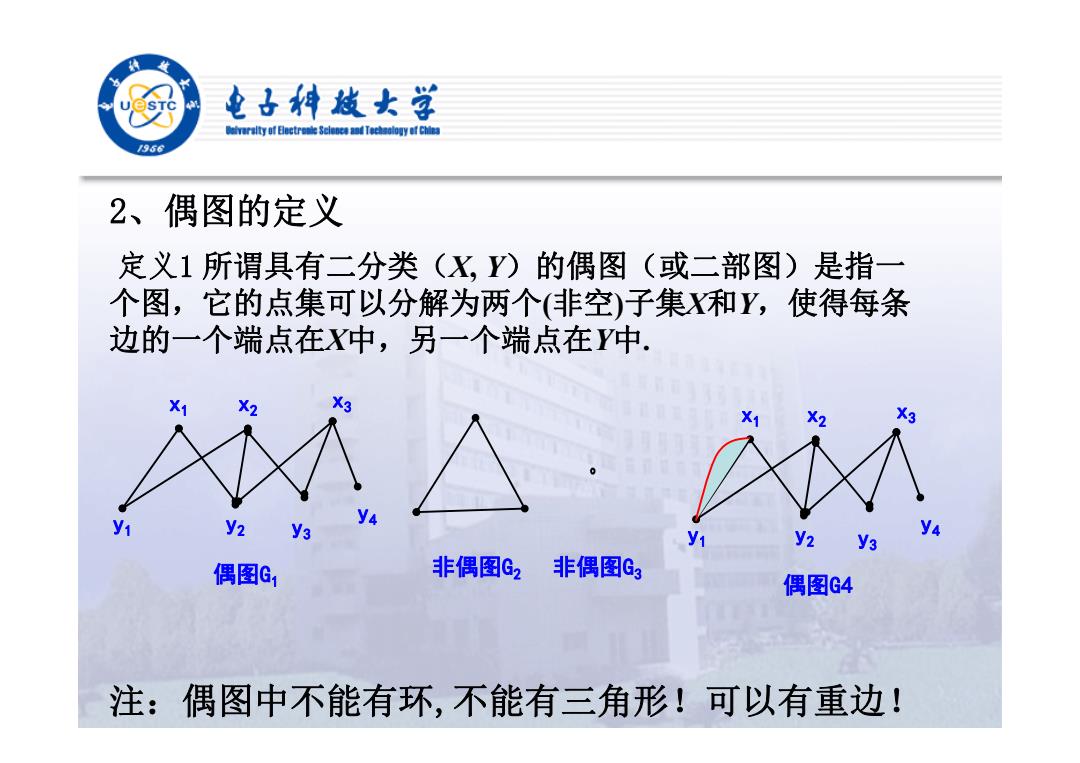
电子科越女学 r街y时Bectrele8 ciad Tecaology af Chins /956 2、偶图的定义 定义1所谓具有二分类(X,Y)的偶图(或二部图)是指一 个图,它的点集可以分解为两个(非空)子集和Y,使得每条 边的一个端点在X中,另一个端点在Y中. X1 X2 X3 X1 X2 X3 y2 y3 y2 y3 偶图G1 非偶图G2 非偶图Gg 偶图G4 注:偶图中不能有环,不能有三角形!可以有重边!
2、偶图的定义 定义1 所谓具有二分类(X, Y)的偶图(或二部图)是指一 个图,它的点集可以分解为两个(非空)子集X和Y,使得每条 边的一个端点在X中,另一个端点在Y中. y4 x1 x2 x3 y3 y1 y2 偶图G1 非偶图G2 非偶图G3 注:偶图中不能有环,不能有三角形!可以有重边! y4 x1 x2 x3 y3 y1 y2 偶图G4