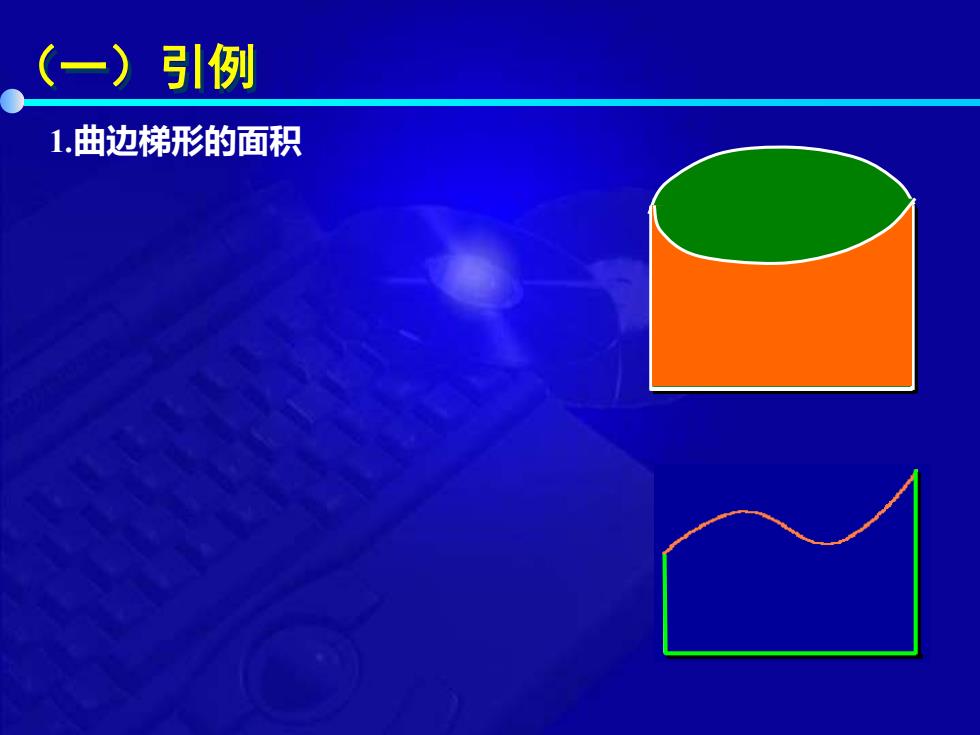
(一)引例 1.曲边梯形的面积
(一)引例 1.曲边梯形的面积
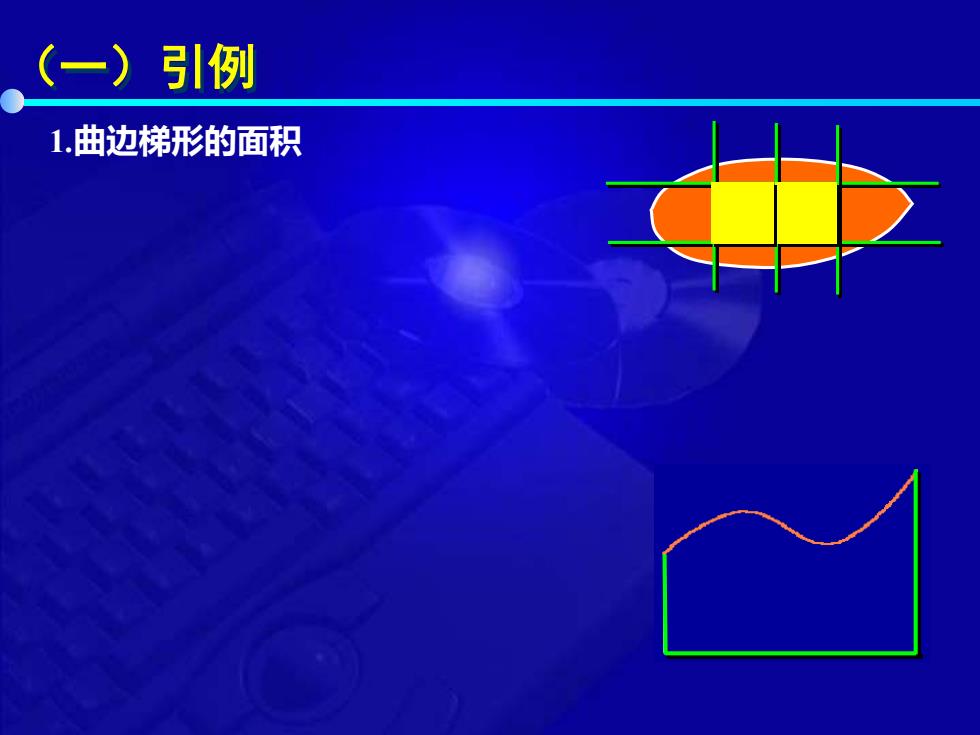
(一)引例 1.曲边梯形的面积
(一)引例 1.曲边梯形的面积
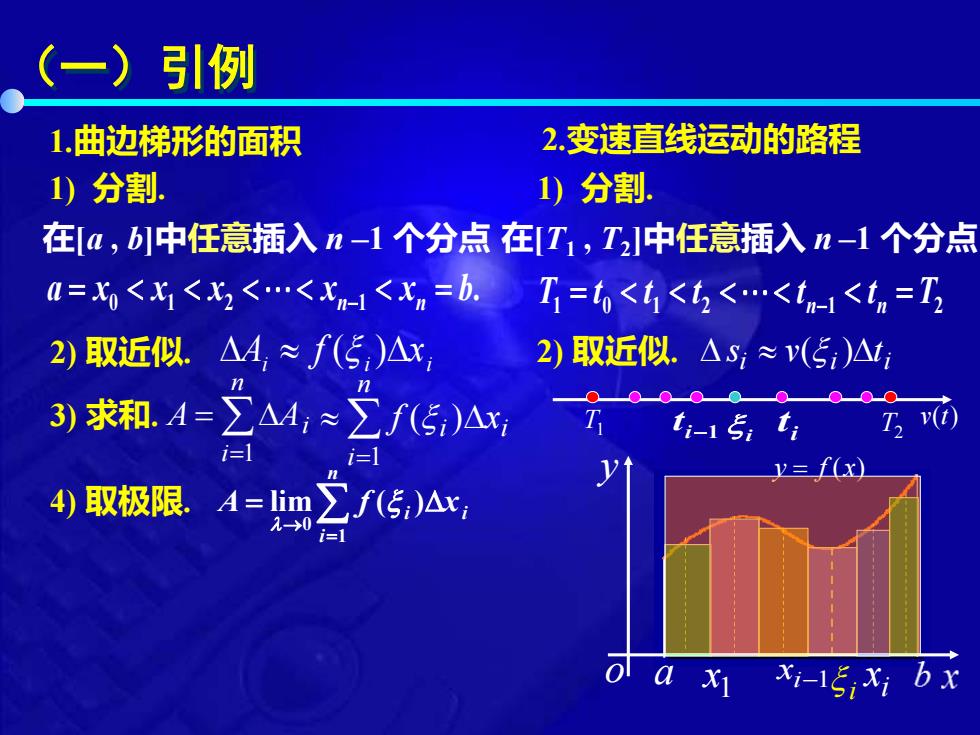
(一)引例 1.曲边梯形的面积 2.变速直线运动的路程 1)分割. 1)分割. 在a,b1中任意插入n-1个分点在IT1,T2]中任意插入n-1个分点 4=X<x<x<<XH<x=b.T=t<t<t<.<t<t=T 2)取近似.△4,≈f(5,)△x 2)取近似.△S,≈v(5)△t 3)求和.A=∑A4,≈∑f(5)△x i=l 三fx 4)取极限.A=1im∑f(传,)△x, i=l ol a x xi-1xi bx
(一)引例 a y o 1) 分割. 在[a , b]中任意插入 n –1 个分点 0 1 2 1 . n n a x x x x x b − = = 2) 取近似. ( ) A f x i i i 3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 0 1 lim ( ) n i i i A f x → = = 1 x i xi−1 x i y = f (x) 1.曲边梯形的面积 2.变速直线运动的路程 1) 分割. T1 T2 v t( ) i 1 t − i t i i i i 2) 取近似. s v( )t 在[T1 , T2 ]中任意插入 n –1 个分点 T t t t t t T 1 0 1 2 1 2 n n − = =
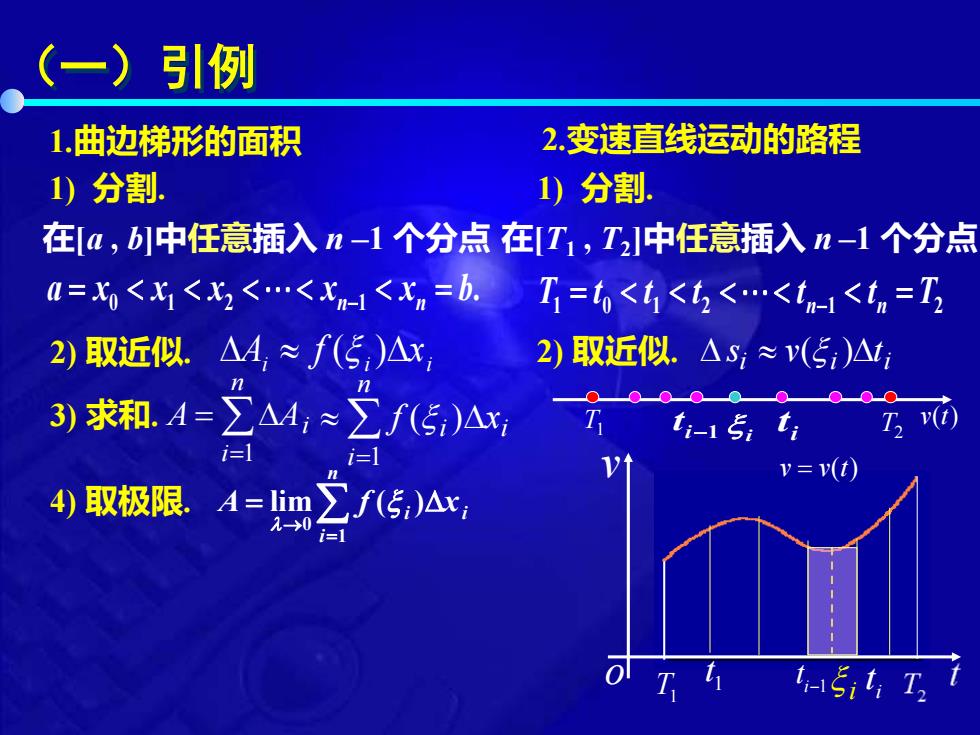
(一)引例 1.曲边梯形的面积 2.变速直线运动的路程 1)分割. 1)分割. 在a,b中任意插入n-1个分点在IT1,T中任意插入n-1个分点 4=X<X<x<<X<x=b.T=t<t<t<.<t<t=T 2)取近似.△4,≈f(5,)△x, 2)取近似.△S,≈v(5,)△ 3)求和.A=∑A4,≈∑f(5)△x i=l i=l v=(t) 4)取极限.A=1im∑f(5,)△x, →0 i=l tasit:T
(一)引例 T1 v o 1) 分割. 在[a , b]中任意插入 n –1 个分点 0 1 2 1 . n n a x x x x x b − = = 2) 取近似. ( ) A f x i i i 3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 0 1 lim ( ) n i i i A f x → = = 1 t i i 1 t t − i v v t = ( ) 1.曲边梯形的面积 2.变速直线运动的路程 1) 分割. T1 T2 v t( ) i 1 t − i t i i i i 2) 取近似. s v( )t 在[T1 , T2 ]中任意插入 n –1 个分点 T t t t t t T 1 0 1 2 1 2 n n − = =

(一)引例 1.曲边梯形的面积 2,变速直线运动的路程 )分割, 1)分割 在[a,中任意插入n-1个分点在T1,T1中任意插入n-1个分点 何问题 <U=T 取近以 物理问题 )△t 3)求和.A= ∑A4≈∑f(5)Ax,3)求和. S≈∑(5)△ = 1= )取极限。 A=im∑f(5:)△x 4)取极限.s=1im∑v(传)△1 20 不同点:背景不同
(一)引例 1) 分割. 在[a , b]中任意插入 n –1 个分点 0 1 2 1 . n n a x x x x x b − = = 2) 取近似. ( ) A f x i i i 3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 0 1 lim ( ) n i i i A f x → = = 1.曲边梯形的面积 2.变速直线运动的路程 1) 分割. i i i 2) 取近似. s v( )t 在[T1 , T2 ]中任意插入 n –1 个分点 T t t t t t T 1 0 1 2 1 2 n n − = = 3) 求和. 4) 取极限. 几 何 问 题 物 理 问 题 不同点:背景不同