
·体系达平衡时,体系中的每个局城也达热力学 平衡,平衡的条件只需用T,等强度性质来描 述. ·一个多组分体系的状态原则上可以用T,PX1) X2X等强度量描述.但体系达平衡后,有各种限 制条件,故描述体系状态所需的变量数不会这 么多,体系的独立变量数会大为减少 ·对于一般的化学体系,可以不考虑除T,以外的 环境条件因素,如电场,磁场,重力场等等.故在 计算体系的独立变量数时,这些因素可以不计
• 体系达平衡时,体系中的每个局域也达热力学 平衡,平衡的条件只需用T,p,i等强度性质来描 述. • 一个多组分体系的状态原则上可以用T,p,x1 , x2.xi等强度量描述.但体系达平衡后,有各种限 制条件,故描述体系状态所需的变量数不会这 么多,体系的独立变量数会大为减少. • 对于一般的化学体系,可以不考虑除T,p以外的 环境条件因素,如电场,磁场,重力场等等. 故在 计算体系的独立变量数时,这些因素可以不计

相律的推导 ·设一热力学体系,含有S种物质,并有Φ个相共存 ·首先假设:每个物种在每个相中均存在 ·体系最多可能有的变量数: ·体系共含Φ个相,每个相中含有S种化学物质,故 共有SΦ个浓度,再加上环境变量T,p,最多可能 有的变量数为: ·总变量数: SΦ+2 ·注意:这些变量不都是必需的!
相律的推导 • 设一热力学体系,含有S种物质,并有个相共存. • 首先假设: 每个物种在每个相中均存在 • 体系最多可能有的变量数: • 体系共含个相,每个相中含有S种化学物质,故 共有S个浓度,再加上环境变量T,p,最多可能 有的变量数为: • 总变量数: S+2 • 注意:这些变量不都是必需的!

但这$Φ+2个变量不全是独立变量,相互间满足 一些关系式。 每列出一个独立的关系式, 意味着可以减少一个变量。 。变量之间存在的关系有: ·1.每一相各组分浓度必满足关系式: ● X1+X2+.+X=1 (a相) ·体系共有Φ个相,故有Φ个类似的方程.变量数需 减去Φ
• 但这S+2个变量不全是独立变量,相互间满足 一些关系式。 • 每列出一个独立的关系式, 意味着可以减少一个变量。 • 变量之间存在的关系有: • 1. 每一相各组分浓度必满足关系式: • x1 + x2 +.+ xs =1 (相) • 体系共有个相,故有个类似的方程. 变量数需 减去
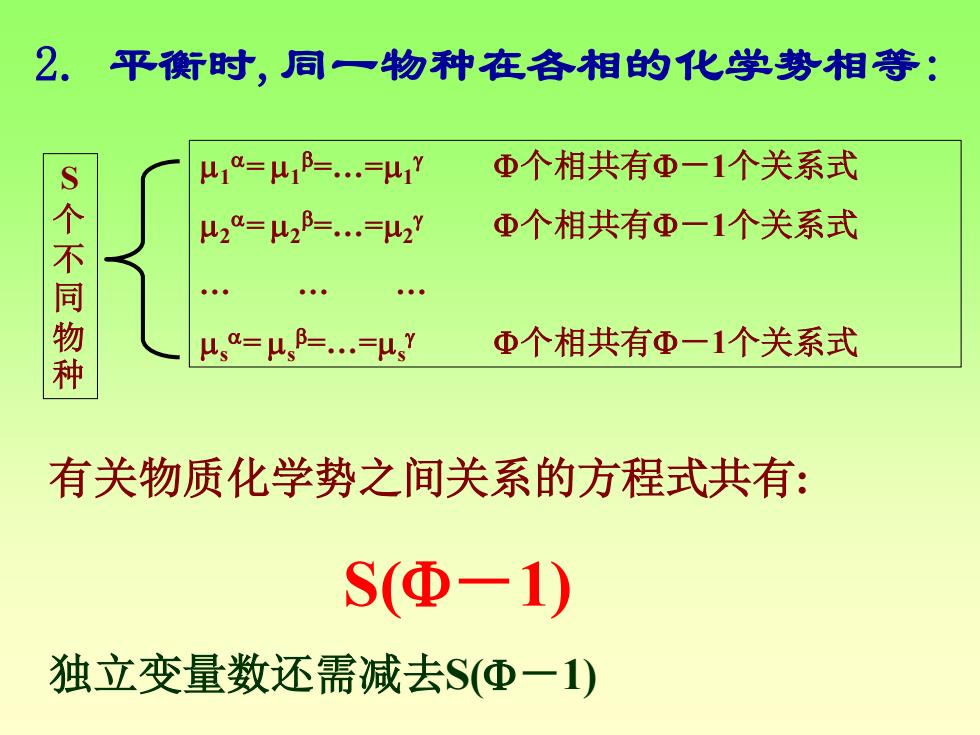
2.平衡时,同一物种在各相的化学势相等: u0=μ1==u Φ个相共有Φ一1个关系式 S个不同物种 28=2==2 Φ个相共有Φ一1个关系式 μ,0=u、==H, Φ个相共有Φ一1个关系式 有关物质化学势之间关系的方程式共有: S(Φ-1) 独立变量数还需减去S(Φ一1)
2. 平衡时,同一物种在各相的化学势相等: 1 = 1 =.=1 个相共有-1个关系式 2 = 2 =.=2 个相共有-1个关系式 . . . s = s =.=s 个相共有-1个关系式 S 个 不 同 物 种 有关物质化学势之间关系的方程式共有: S(-1) 独立变量数还需减去S(-1)