
赫氏自由能 吉氏自由能 热力学基本关系式
赫氏自由能 吉氏自由能 热力学基本关系式

第六节赫氏自由能和吉氏自由能 ·熵判据从原理上虽然可以解决一) 自然过程的方向和限度问题,但使 用起来殊不方便,为了热力学判据 使用的方便,人们由熵函数发展出 赫氏自由能和吉氏自由能, 赫氏自由能用于等温等容过程。 ·吉氏自由能用于等温等压过程
第六节 赫氏自由能和吉氏自由能 • 熵判据从原理上虽然可以解决一切 自然过程的方向和限度问题, 但使 用起来殊不方便, 为了热力学判据 使用的方便, 人们由熵函数发展出 赫氏自由能和吉氏自由能. • 赫氏自由能用于等温等容过程. • 吉氏自由能用于等温等压过程
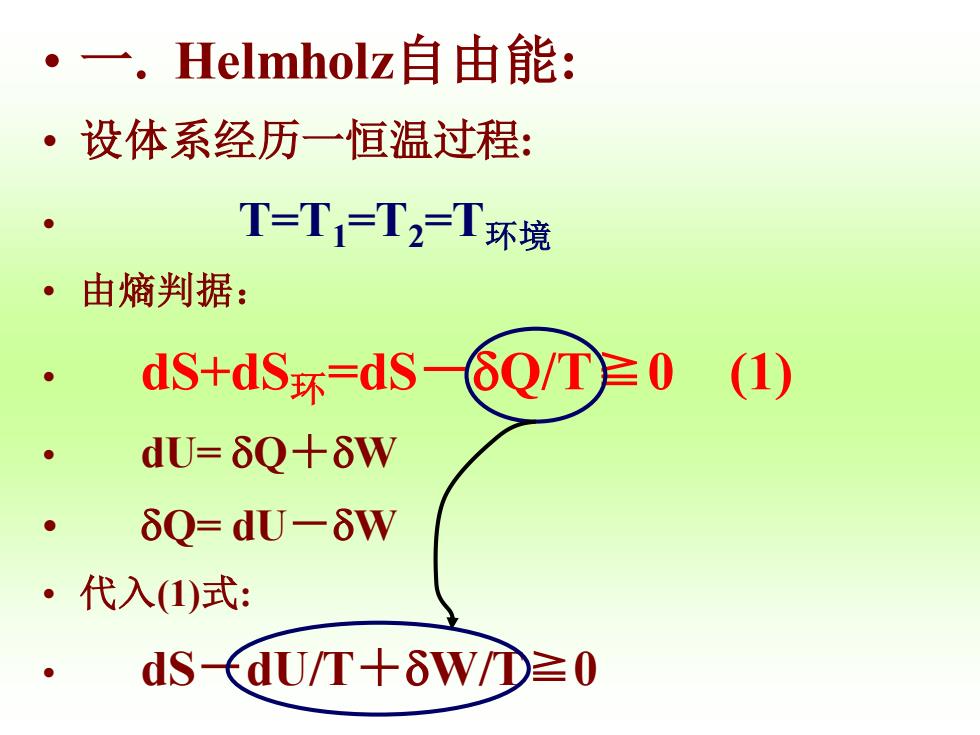
·一.Helmholz自由能: ·设体系经历一恒温过程: T=T=T2=T环境 ·由熵判据: ● dS+dS环=dS-6Q/T≥0 (1) ● dU=δQ+δW ● δQ=dU-δW ·代入(1)式: dS(dU/T+δW①≥0
• 一. Helmholz自由能: • 设体系经历一恒温过程: • T=T1=T2=T环境 • 由熵判据: • dS+dS环=dS-Q/T≧0 (1) • dU= Q+W • Q= dU-W • 代入(1)式: • dS-dU/T+W/T≧0

·两边同乘以T: ● TdS-dU+δW≥0 等温过程: TdS=d(TS) ● dTS)-dU≥-δW ● 一d(U一TS)≥一δW 令: F≡U一TS (2) ·F:赫氏自由能(Helmholz free energy) ·由德国科学家赫姆霍兹首先定义
• 两边同乘以T: • TdS-dU+W≧0 • 等温过程: • TdS=d(TS) • d(TS)-dU ≧ -W • -d(U-TS) ≧ -W • 令: F≡U-TS (2) • F :赫氏自由能(Helmholz free energy) • 由德国科学家赫姆霍兹首先定义

·将F代入熵判据式: 一dF≥一δW (3) ·或一△F≥一W 恒温过程 (4) (④F)I,y≤W:等温,等容,W体=O (5) ·对于等温,等容且无有用功的过程: △F≤0 (dT=0,dV=0,W=0) (6) 。 (⑥)式也为热力学判别式,其物理含义为: 在等温,等容,不作有用功的条件下,体 系的赫氏自由能只会自发地减少
• 将F代入熵判据式: • -dF≧ - W (3) • 或 -F≧ -W 恒温过程 (4) • (F)T,V≦Wf 等温,等容,W体=0 (5) • 对于等温,等容且无有用功的过程: • F≦0 (dT=0, dV=0, Wf=0) (6) • (6)式也为热力学判别式,其物理含义为: • 在等温,等容,不作有用功的条件下, 体 系的赫氏自由能只会自发地减少