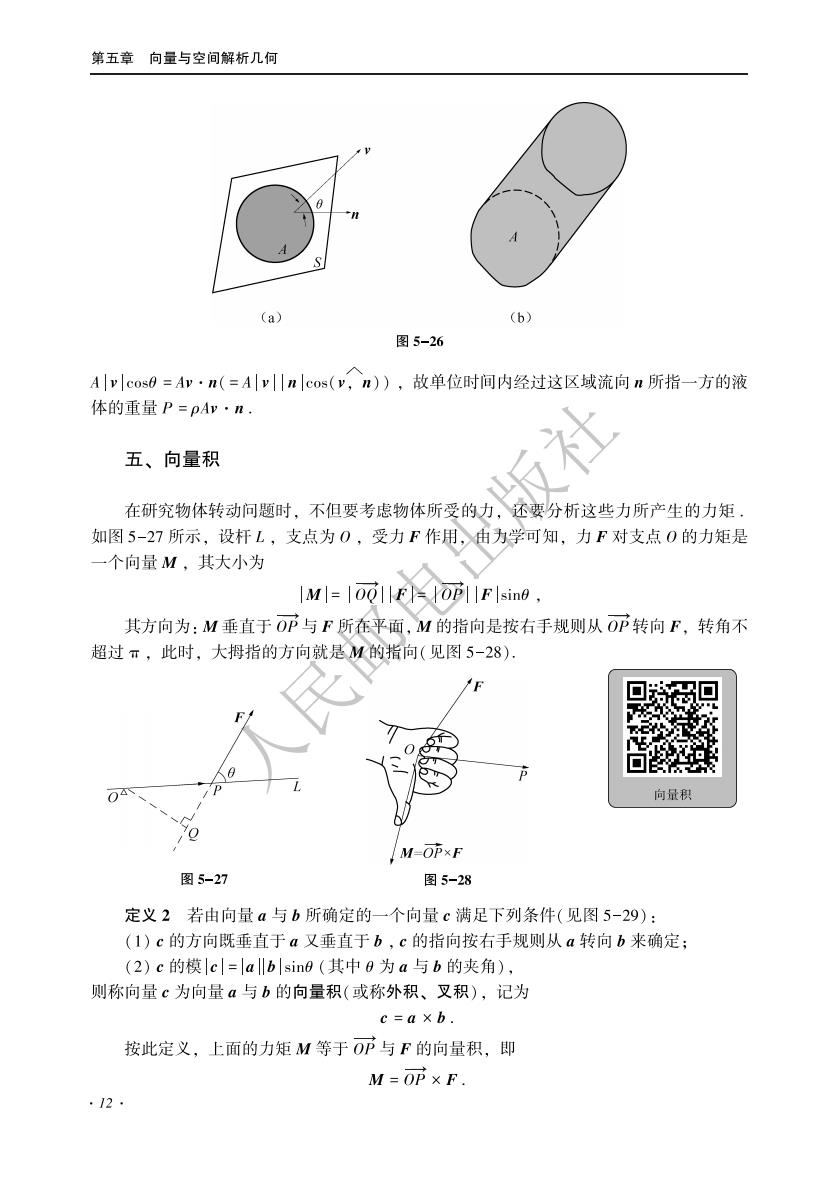
第五章向量与空间解析几何 (a) 6 图5-26 Acos0=Ar·n(=Av川ncos(y,n),故单位时间内经过这区域流向n所指一方的液 体的重量P=pAv·n 五、向量积 在研究物体转动问题时,不但要考虑物体所受的力,还要分析这些力所产生的力矩。 如图5-27所示,设杆L,支点为0,受力F作用,由为学可知,力F对支点0的力矩是 一个向量M,其大小为 IMI=10011FYOPIIFIsine, 其方向为:M垂直于OP与F所在平面,M的指向是按右手规则从OP转向F,转角不 超过π,此时,大拇指的方向就是M的指向(见图5-28). ▣8▣ 向量积 M-OPxF 图5-27 图5-28 定义2若由向量a与b所确定的一个向量c满足下列条件(见图5-29): (1)c的方向既垂直于a又垂直于b,c的指向按右手规则从a转向b来确定; (2)c的模|c=allblsine8(其中g为a与b的夹角), 则称向量c为向量a与b的向量积(或称外积、叉积),记为 c=a×b. 按此定义,上面的力矩M等于O与F的向量积,即 M=O×F 12
人民邮电出版社

第一节向量及其运算 根据向量积的定义,即可推得 (1)a×a=0; (2)设a、b为两非零向量,则a/b的充分必要条 件是a×b=0. 证(1)a×al=lallalsin(a,a)=0. (2)→已知a/b,即(a,b)=0或(a,b)=T,故 sin(a,B)=0, 即la×b=|allblsin(a,b)=0,a×b=0. =若已知a×b=0,即 lallblsin(a.B)=0. 故sin(a,b)=0,(a,b)=0或(a,b)=r,因此 a//b. 由此可知,空间三点A、B、C共线的充分必要条件 图5-29 是AB×AC=0. 向量积满足下列运算规律 (1)a×b=-b×a: (2)分配律(a+b)×c=a×c+b×c; (3)结合律A(a×b)=(Aa)×b=aX)CA为实数) 证明请读者白己完成, 下面我们来推导向量积的坐标表式 设a=(a,a)=ai+tk,b=(b,b,b,)=b,i+b,j+bk,则 a×b=(ai+a,j+ak)×(b,i+b,j+b,k) =a,b,i×i+0b×j+a,b.i×k+a,bj×i+a,b,j×j+a,bj×k +bk×i+a,b,k×j+a,bk×k, 注意到i×i=j×j=k×k=0,i×对j=k,j×k=i,k×i=j,并利用二、三阶行列式的 计算公式(见本章的拓展阅读),则有 a x b =ab k a b:j-a,b k +a,bi+a.b,j-a.b i =(a,b:-a,b)i-(a,b:-a,b,)j (a,by ab,)k 0。a:+(-1)6bP+,3k b,6 b,by ii k a,ay a. bb,b: 由此可得:若a≠0,b|≠0,则 a×b=0a/b台a,b:-a:b,=0,ab-ab=0,a,b,-a,b,=0 即会-(亦即a=A,A为实数 ·13
人民邮电出版社

第五章向量与空间解析几何 例13求与a=3i-2+4k,b=i+j-2k都垂直的单位向量 i jki j k 解c=a×b=axa,a:=3-24=10i+5k b.6,611-2 因为1小o5,所后原+) 例14在顶点为A(1,-1,2)、B(5,-6,2)和C(1,3,-1)的三角形中,求AC边 上的高BD. 解AC=(0,4,-3),AB=(4,-5,0),根据向量积的定义,可知三角形ABC的 面积为 s=cln∠4=C×=分s+12+16-空 又 s-21AC( 所以空=5小BD,从面1BD=5 例15设向量m,n,p两两垂直,符合右手规则且 |m=4,1n=2,pl3, 计算(m×n)·p 1x1(n心×2x1-8,依知m×n与p同向,则 0=(m×n,p)=0,(mxm)·p=|m×n1|pl cos0=8·3=24. 例16设纲刚体以等角速度ω绕1轴旋转,计算刚体上一点M的线速度 解刚体绕!轴旋转时,我们可以用在1轴上的一个向量ω表示角 速度,它的大小等于角速度的大小,它的方向由右手规则写出,即右 手握住1轴,当右手的四个手指的转向与刚体的旋转方向一致时,大 拇指的指向就是0的方向,如图5-30所示.设点M至旋转轴1的距离 为a,再在1轴上任取一点0,作向量r=0并以0表示w与r的夹 角,则a=lr1sin0.设线速度为",那么由物理学上线速度与角速度 0 的关系可知,"的大小为 图5-30 v的方向垂直于通过M点与1轴的平面,即v垂直于w与r; 又的指向是使w、r、y符合右手规则,因此有 y=ωXr. 六、混合积 定义3设已知三向量a、b、c,先作向量积a×b,再作数量积(a×b)·c,记作 14
人民邮电出版社

第一节向量及其运算 [abc],称为三个向量a、b、c的混合积 下面我们来看混合积的坐标表示式. a=(a.a,a.)=a,i+ayj+ak,b=(b.by,b.)=bi+bj+bk c=(ex,cy,e:)=ci+ej+ck, i a×b=axa,a ex cy e: bs by b. a,ay a:b,by b. b,by b.=c.e,c. ex ey c:ax ay a 由此可得 [abc]=(axb)·c=(b×c)·a=(c×a)·b=c·(ax①=a·(b×c)=b·(c×a) 混合积是一个数,它的绝对值表示以向量a、b,c为棱的平行六面体的体积。 若a、b、c成右手系时,[abc]≥0:若a、bc成左手系时,[abc]≤0. 事实上,由于|a×b=allblsin(a,b)表示边长为|a、|b1的平行四边形面积(见 图5-31),若a×b与c在a、b所在平面的侧,即a×b与c之间的夹角0为锐角,则 (a×b)·c=|a×b|lelcose0>0:若axb与c在a、b所在平面的两侧,即a×b与c之间的 夹角0为纯角,则(a×b)·c=a×bc cosf<0.而|elcose0为平行六面体的高,因此 V=±|a×bllefcose0=±[abc](见图5-32). axb a×b S-laxbl 图5-31 图5-32 非零向量a、b、c共面的充分必要条件是[abc]=0. 由此可知,空间四点A、B、C、D共面的充分必要条件是[AB AC A而)=0. 例17已知(a×b)·c=2,计算[(a+b)×(b+c)]·(c+a). 解[(a+b)×(b+c)]·(c+a)=[a×b+a×c+b×b+b×c]·(c+a) =(a×b)·c+(a×c)·c+(b×b)·c+(b×c)·c +(axb).a+(a×c)·a+(b×b)·a+(b×c).a =(a×b)·c+0+0+0+0+0+0+(a×b)·c =2(a×b)·c=4. ·15
人民邮电出版社