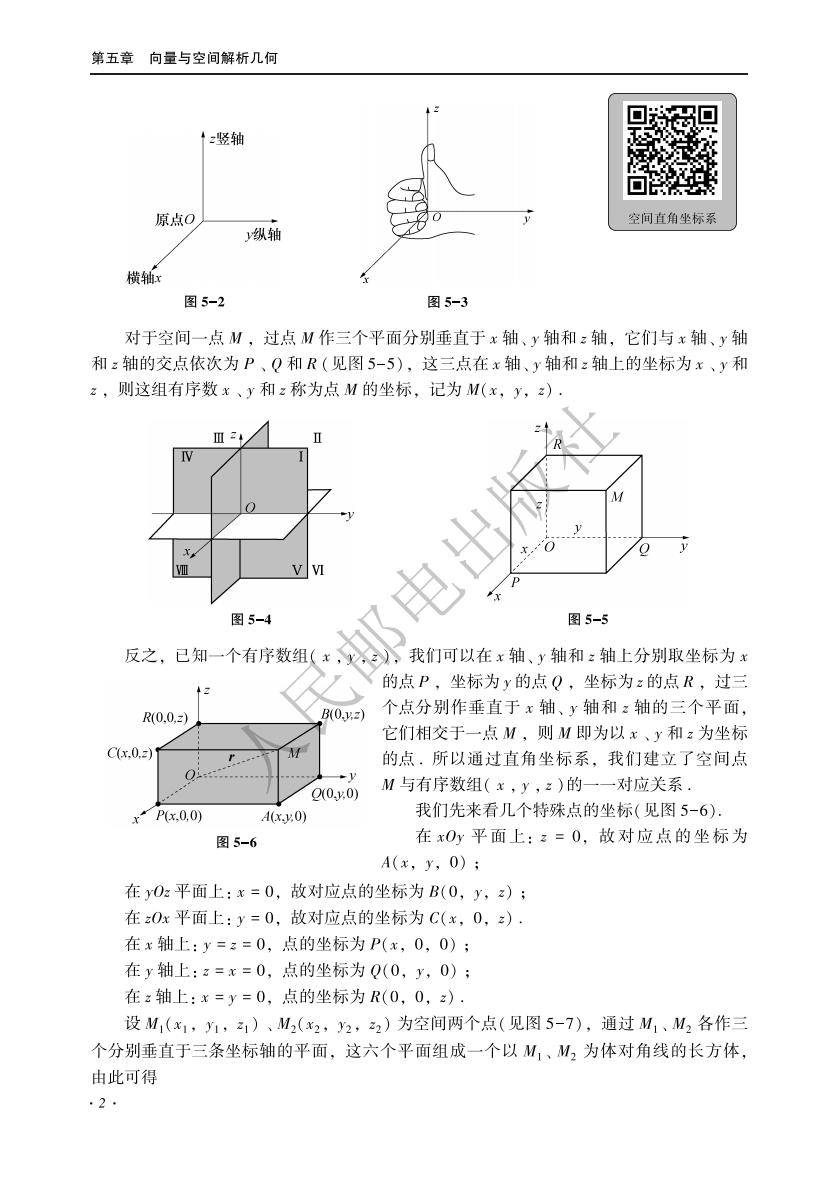
第五章向量与空间解析几何 竖轴 原点0 纵轴 空问直角坐标系 横轴 图5-2 图5-3 对于空间一点M,过点M作三个平面分别垂直于x轴、y轴和:轴,它们与x轴、y轴 和:轴的交点依次为P、Q和R(见图5-5),这三点在x轴、y轴和:轴上的坐标为x、y和 :,则这组有序数x、y和:称为点M的坐标,记为M(x,y,)· 图5-5 反之,已知一个有序数组(x,我们可以在x轴、y轴和:轴上分别取坐标为 的点P,坐标为y的点Q,坐标为z的点R,过 12 R0.0, B0.) 个点分别作垂直于x轴、y轴和:轴的三个平面 它们相交于一点M,则M即为以x、y和:为坐标 Cx.0.=) 的点,所以通过直角坐标系,我们建立了空间点 Q00) M与有序数组(x,y,z)的一一对应关系. Px0,0) M(xv:0) 我们先来看几个特殊点的坐标(见图5-6). 图5-6 在xOy平面上::=0,故对应点的坐标为 A(x,y,0); 在yO:平面上:x=0,故对应点的坐标为B(0,y,z); 在z0x平面上:y=0,故对应点的坐标为C(x,0,) 在x轴上:y=:=0,点的坐标为P(x,0,0): 在y轴上:a=x=0,点的坐标为Q(0,y,0): 在:轴上:x=y=0,点的坐标为R(0,0,). 设M1(x,1,1)、M(x2,2)为空间两个点(见图5-7),通过M1、M2各作三 个分别垂直于三条坐标轴的平面,这六个平面组成一个以M,、M2为体对角线的长方体, 由此可得 2+
人民邮电出版社

第一节向量及其运算 d2=1M1M212=(x2-x1)2+(2-y1)2+(2-41)2, 即 d=M,M1=/(2-x)2+(2-y)2+(2-)2. 例1证明以点M1(4,3,1)、M2(7,1,2)及 M(5,2,3)为顶点的三角形是等腰三角形. 证1MM1=√(7-4)2+(1-3)2+(2-1) =14, 1M2M1=(5-7)2+(2-1)2+(3-2) 图5-7 =6, 1MM1=√(4-5)2+(3-2)2+(1-3)2=√6 即|M2=MM1,因此该三角形是等腰三角形。 例2在z轴上求与两点A(-4,1,7)和B(3,5,-2)等距离的点 解设所求点的坐标为M(0,0,),由A=B即 0+42+(0-)2+(-7=3-05702+(-2-, 得:14 14. ,因此所求点的坐标为M(0,0, 9· 二、向量的运算 1.向量的投影及投影定理 将非零向量α、b的始点重合,在两向量的所在平面上,若一个向量逆时针方向转过 角度0后可与另一个向量正向重合(见图5-8),则称0为向 量a、b的夹角,记作(a,b),即 0=(a,b)=(b,a)(0≤0≤m). 对于向量a、b,如果它们的夹角=0或=,则称 这两个向量平行,记为a/b,其中两个向量指向一致时 6=0,指向相反时0=T.指向相同的两个平行向量a、b如 果还满足a=b,那么这两个向量相等,记为a=b.与向 图5-8 量a的模相同,但方向相反的向量叫作a的负向量,记作-a 对于一向量与一轴的夹角,可将其中一轴看作向量 按两向量之间的夹角来度量:对于两个轴之间的夹角,则看作两向量的夹角. 通过空间一点A作与u轴垂直的平面(见图5-9),该平面与u轴的交点A'称为点A在 u轴上的投影 如果向量AB的始点A与终点B在u轴上的投影分别为A'、B(见图5-10),则u轴上 的有向线段A'B的值A'B'称为向量A店在u轴上的投影,记作P.AB=A'B',u轴称为投 影轴. 3
人民邮电出版社
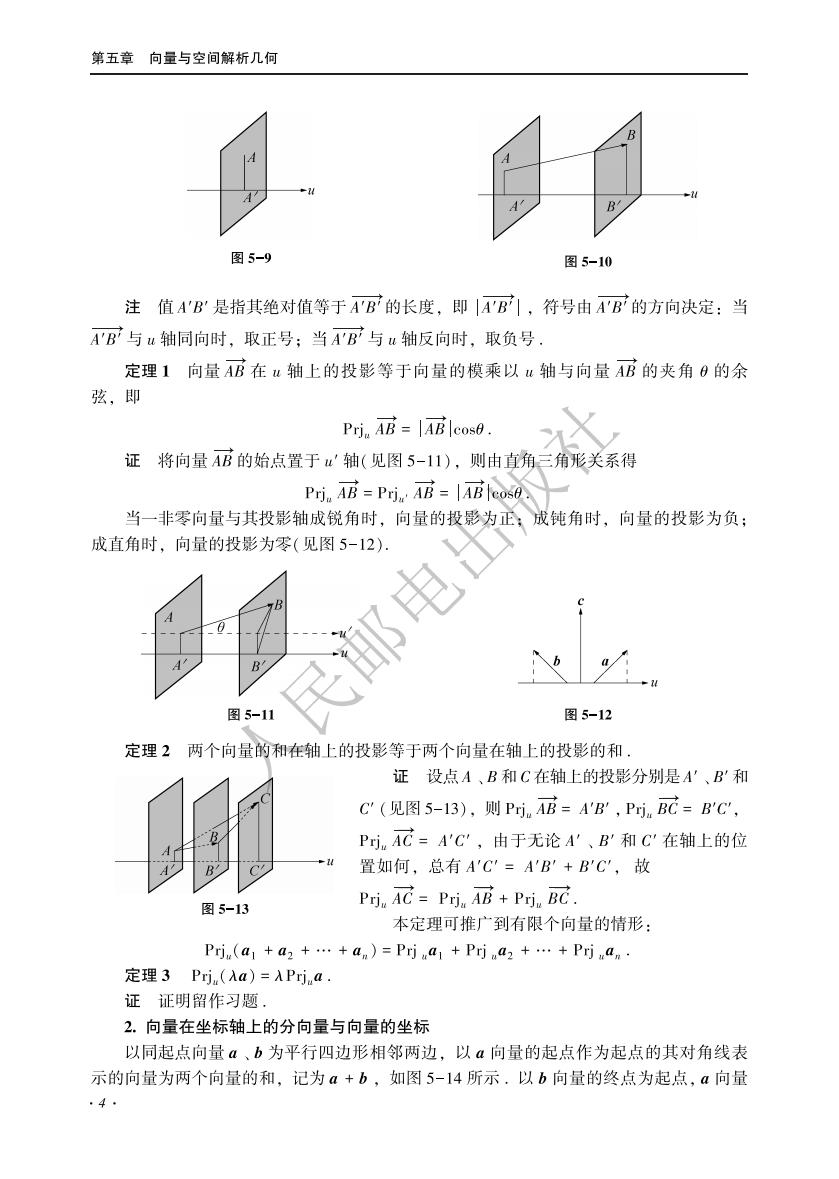
第五章向量与空间解析几何 图5-9 图5-10 注值A'B是指其绝对值等于A'B的长度,即|A'B1,符号由A'B的方向决定:当 AB与u轴同向时,取正号:当B与u轴反向时,取负号 定理1向量AB在u轴上的投影等于向量的模乘以u轴与向量AB的夹角0的余 弦,即 Pri.AB=AB cos0. 证将向量A店的始点置于4轴(见图5-11),则由直角三角形关系得 Pri.AB Pri AB=AB cose. 当一非零向量与其投影轴成锐角时,向量的投影为正成钝角时,向量的投影为负: 成直角时,向量的投影为零(见图5-12). 图5-11 图5-12 定理2两个向量的和在轴上的投影等于两个向量在轴上的投影的和. 证设点A、B和C在轴上的投影分别是'、B'和 C(见图5-13),则Pj.A店=A'B',P可j.B元=B'C Prj,AC=A'C',由于无论A'、B'和C'在轴上的位 置如何,总有A'C=A'B'+B'C',故 图5-13 Prj.AC Prj.AB Prj.BC 本定理可推广到有限个向量的情形: Prj(a1+a2+.+an)=P可ja1+Pja2+.+Pjan 定理3Prj,(Aa)=APrja 证证明留作习题. 2.向量在坐标轴上的分向量与向量的坐标 以同起点向量a、b为平行四边形相邻两边,以a向量的起点作为起点的其对角线表 示的向量为两个向量的和,记为a+b,如图5-14所示,以b向量的终点为起点,a向量 4
人民邮电出版社
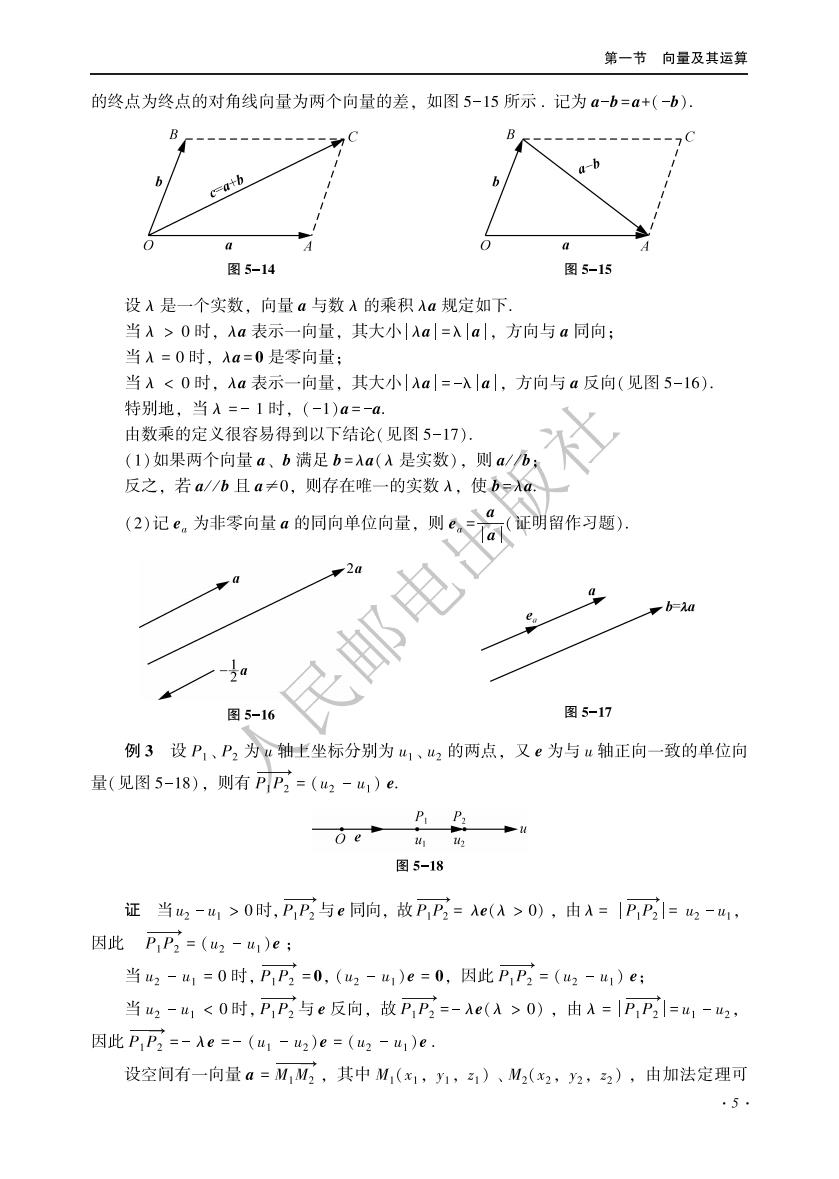
第一节向量及其运算 的终点为终点的对角线向量为两个向量的差,如图5-15所示,记为a-b=a+(-b) c-atb 图5-14 图5-15 设入是一个实数,向量a与数A的乘积a规定如下. 当A>0时,Aa表示一向量,其大小Aa=入al,方向与a同向: 当A=0时,Aa=0是零向量; 当A<0时,Aa表示一向量,其大小a=-入|a,方向与a反向(见图5-16) 特别地,当A=-1时,(-1)a=-a. 由数乘的定义很容易得到以下结论(见图5-17). (1)如果两个向量a、b满足b=Aa(A是实数),则a/b: 反之,若a/h且a≠0,则存在唯一的实数入,使b (2)记e.为非零向量a的同向单位向量,则c,a (证明留作习题) 2a b- -5a 图5-16 图5-17 例3设P、P2为u轴上坐标分别为山1、山2的两点,又e为与u轴正向一致的单位向 量(见图5-18),则有PP=(2-4)e. 图5-18 证当w2-1>0时,P与e同向,故P,P=A(A>0),由A=1PP=2-4, 因此P,P=(山2-)e; 当42-41=0时,PP=0,(2-u1)e=0,因此PD=(42-41)e: 当42-41<0时,PP与e反向,故PP=-e(A>0),由入=|PP1=41-42 因此P乃=-Ae=-(u1-)e=(u-4)e 设空间有一向量a=MM,其中M,(x1,)、M2(x2,2,2),由加法定理可 ,5
人民邮电出版社

第五章向量与空间解析几何 知a可分解为三个分别平行于x轴、y轴和z轴的向量ax、a,和a,它们称为a在x轴、y 轴和:轴的三个分向量.显然a=a,+a,+a,(见图5-19) 图5-19 设-1=a,-=a,-41=4,则有 Prj,a=Prj,a,=x2-xa Prj,a Prj,a,=y2, Prja =Prj.a:=a. 若用i、方和k分别表示与x轴、y轴和轴正向一致的三个单位向量,称它们为基本单 位向量,则有a,=(-i,a,发1,a,=(-k,因此 a=a,+a,+a,=(x2x1)it2-y1)j+(2-1)k=a,i+aj+a,k, 称上式为向量a按甚本单位向量的分解式或a的向量表示式, 一方面,从向量a可以唯二定出它在三条坐标轴上的投影a,、a,和a:,另一方面, 从a、a,和a,可以唯定出向量a,这样有序数组a,、a,、a,就与向量a一一对应,于是 将a,、a,、a,称为向量a的坐标,记为a=(a,a,a),也称为向量a的坐标表示式 以M,(x1,1)为始点、M2(2,y2,2)为终点的向量记为 M1M=(x2-x1,y2-1,32-)· 特别地,M(x,y,z),向径r=0O7=(x,y,z)(见图 5-20) 对于向量的运算也可化为对坐标的数量运算。 设向量a=(a,a,a,),b=(b,b,b),则 a±b=(a,i+a,j+a.k)±(b,i+b,j+bk) =(a±b,)i+(a,±b,j+(a±b)k =(a,±bx,ay±b,a±b); Aa=A(a,i+a,j+ak)=(Aa,)i+(Aa,)j+(Aa.)k= (Aax,Aa,Aa). 图5-20 例4设A(x1,1,)和B(x2,y2,2)为空间两
人民邮电出版社