
4.公法线 齿轮在加工、检验时,常用测量公法线长度的方法来判断和保证齿轮的加工精度。如图615 所示,卡尺在任意位置上卡住齿轮的两条反向渐开线,则卡尺之间的距离就是两齿廊的公法线长 度W,其中k为测量时卡尺跨过的齿数。 由式(6-11)可知,公法线长度应该等于基圆上的弧长,即队=(依-)乃,+5。跨测齿数k 的选取应保证卡尺的卡脚与渐开线齿廊相切。跨测齿数太多,卡尺将顶住齿顶圆,不能保证卡尺 与齿廓相切:跨测齿数太少,卡尺将顶在齿轮的齿根圆上,也不能保证卡尺与齿轮相切。一般跨 测齿数为k=a/180°+0.5。当a=20°时,k-0.111上+0.5。 5.节圆和标准中心距 根据渐开线的性质,两个齿轮啮合点的公法线一定与两个齿轮的基圆同时相切。如0所示, 当两个齿轮的基圆与中心位置确定后,两基圆的公切线(同一侧)只有一条n-,所以两个齿轮 所有啮合点的公法线都是同一条直线-n,将n-n称为啮合线。 u 图6-15公法线长度检测 图616啮合线 啮合线m-n与两齿轮中心连线的交点称为节点(pitch point),则以O1和O2为圆心,过节点 所作的两个圆称为两齿轮的节圆(pitch circle),节圆的直径和半径分别用d和r表示。当节圆的 直径与分度圆直径相同时,即”=d时,则两齿轮的分度圆相切,称之为标准中心距安装。此时 a=2(d+d)=m6,+) (6-13) 6.4.4齿条和内齿轮的尺寸 1.齿条 如图617所示,齿条相当于基圆无穷大时的齿轮。齿轮的分度圆、齿顶圆、齿根圆变成了 齿条的分度线、齿顶线和齿根线。齿条与齿轮相比,有以下几个特点: (1)渐开线齿廓变成了直线齿廓,压力角α处处相等,且等于其齿形角。 116
116 4.公法线 齿轮在加工、检验时,常用测量公法线长度的方法来判断和保证齿轮的加工精度。如图 6-15 所示,卡尺在任意位置上卡住齿轮的两条反向渐开线,则卡尺之间的距离就是两齿廓的公法线长 度 Wk ,其中 k 为测量时卡尺跨过的齿数。 由式(6-11)可知,公法线长度应该等于基圆上的弧长,即 k b b W = (k −1) p + s 。跨测齿数 k 的选取应保证卡尺的卡脚与渐开线齿廓相切。跨测齿数太多,卡尺将顶住齿顶圆,不能保证卡尺 与齿廓相切;跨测齿数太少,卡尺将顶在齿轮的齿根圆上,也不能保证卡尺与齿轮相切。一般跨 测齿数为 = /180 + 0.5 k z 。当 = 20 时, k − 0.111z + 0.5。 5.节圆和标准中心距 根据渐开线的性质,两个齿轮啮合点的公法线一定与两个齿轮的基圆同时相切。如 0 所示, 当两个齿轮的基圆与中心位置确定后,两基圆的公切线(同一侧)只有一条 n-n,所以两个齿轮 所有啮合点的公法线都是同一条直线 n-n,将 n-n 称为啮合线。 图 6-15 公法线长度检测 图 6-16 啮合线 啮合线 n-n 与两齿轮中心连线的交点称为节点(pitch point),则以 O1和 O2 为圆心,过节点 所作的两个圆称为两齿轮的节圆(pitch circle),节圆的直径和半径分别用 d ' 和 r' 表示。当节圆的 直径与分度圆直径相同时,即 d' = d 时,则两齿轮的分度圆相切,称之为标准中心距安装。此时 ( + ) 2 1 ( + ) = 2 1 = 1 2 1 2 a d d m z z (6-13) 6.4.4 齿条和内齿轮的尺寸 1.齿条 如图 6-17 所示,齿条相当于基圆无穷大时的齿轮。齿轮的分度圆、齿顶圆、齿根圆变成了 齿条的分度线、齿顶线和齿根线。齿条与齿轮相比,有以下几个特点: (1)渐开线齿廓变成了直线齿廓,压力角 处处相等,且等于其齿形角

(2)齿距处处相等,p=m,p。=peosa。 齿条的其它参数与基本尺寸的计算可参照外齿轮进行 图617齿条 2.内齿轮 如图6-18a所示,内齿轮的轮齿分布在空心圆柱的内表面上。与外齿轮相比,内齿轮有以下 几个特点: (1)轮齿与齿槽的形状刚好与外齿轮相反。 (2)齿顶圆的直径小于齿根圆的直径,,=r-h,r=r+h。 (3)为保证内齿轮的齿顶部分齿廓为渐开线,其齿顶圆的直径应该大于基圆直径,即,≥。。 (4)一个内齿轮与一个外齿轮的啮合称为内啮合,如图6-18b所示,这时两齿轮的标准中 心距a为两齿轮分度圆半径之差,即a=乃-h。 内齿轮的其它参数与基本尺寸的计算也可参照外齿轮进行。 (a)内齿轮 (b)内啮合 图6-18内齿轮与内啮合 6.5渐开线标准圆柱齿轮的啮合传动 6.5.1渐开线齿轮的传动特性 如图6-19所示为一对齿轮的啮合情况,其中O,、O2分别为齿轮1和齿轮2的圆心,。是 117
117 (2)齿距处处相等, p =m , pn = p cos 。 齿条的其它参数与基本尺寸的计算可参照外齿轮进行。 图 6-17 齿条 2.内齿轮 如图 6-18a 所示,内齿轮的轮齿分布在空心圆柱的内表面上。与外齿轮相比,内齿轮有以下 几个特点: (1)轮齿与齿槽的形状刚好与外齿轮相反。 (2)齿顶圆的直径小于齿根圆的直径, a ha r = r − , f hf r = r + 。 (3)为保证内齿轮的齿顶部分齿廓为渐开线,其齿顶圆的直径应该大于基圆直径,即 a b r r 。 (4)一个内齿轮与一个外齿轮的啮合称为内啮合,如图 6-18b 所示,这时两齿轮的标准中 心距 a 为两齿轮分度圆半径之差,即 2 1 a = r − r 。 内齿轮的其它参数与基本尺寸的计算也可参照外齿轮进行。 (a) 内齿轮 (b)内啮合 图 6-18 内齿轮与内啮合 6.5 渐开线标准圆柱齿轮的啮合传动 6.5.1 渐开线齿轮的传动特性 如图 6-19 所示为一对齿轮的啮合情况,其中 O1 、O2 分别为齿轮 1 和齿轮 2 的圆心, 是

齿轮的角速度,K是两齿轮的啮合点,vK,和v,是两齿轮在K点的线速度。由前所述,渐开线 上任意点K的法线,一定与其基圆相切,所以,两齿轮呐合时,其公法线-”一定同时与两个齿 轮的基圆和2相切,切点分别为N,和N2。 根据渐开线的性质可知:K⊥K,NK⊥N1,所以 ∠N2KvK1=∠N,O1K=aK1 同理,∠N2Krk2=∠N2O2K=aK2· 因为两齿轮在K点的公法线-n方向上的速度是相同的,所以 又因为K1=K1,K2=02K2,所以 TKI0 COSOK =20COSaK 将rk1 COSaKI1=b1,k2 cos@K2=2代入上式可得 b01=rb203 再将这一结果代入式(61)得 (6-14) 综合上述分析过程,可见渐开线齿轮具有如下传动特性 1)传动比恒定 由式(6-14)可知,渐开线齿廓的齿轮在任意点K处啮合时,其传动比1都等于两齿轮基圆 半径的反比,是个常量,所以在传动过程中,传动比是个恒定值。 2)中心距具有可分性 由于渐开线齿轮的传动比只与两齿轮的基圆半径相关,而一对齿轮加工完成后,两齿轮的基 圆半径就确定了,所以其传动比也就确定了。如果由于制造、安装或磨损等原因造成中心距发生 了变动,传动比也不会随之变化。这一特性称为渐开线齿轮的中心距可分性,它为齿廓的加工和 齿轮的安装等带来很大的方便,是渐开线齿轮得到广泛应用的原因之一。 3)传力方向不变 两齿廓的接触点K的公法线始终与两个齿轮的基圆相切(为两基圆的公切线),而当两个齿 轮安装好之后,基圆的公切线的位置也随之确定。也就是说两齿廓啮合时的正压力方向(沿 -n)始终不变,这个特点对于齿轮传动过程中的平稳性是非常有利的。 6.5.2新开线齿轮的正确啮合条件 如图6-20所示为一对渐开线齿轮的啮合情况。如前所述,一对渐开线齿廓在任意位置啮合 时,其接触点都应在啮合线NN,上。因此当上一对轮齿在啮合线上B,点接触时,下一对轮齿的 啮合点B,也应该在NN上。由此可以看出,两齿轮能够正确哺合的条件应该是:两齿轮的法 向间距相等,即
118 齿轮的角速度,K 是两齿轮的啮合点, K1 v 和 K2 v 是两齿轮在 K 点的线速度。由前所述,渐开线 上任意点 K 的法线,一定与其基圆相切,所以,两齿轮啮合时,其公法线 n-n 一定同时与两个齿 轮的基圆 b1 r 和 b2 r 相切,切点分别为 N1 和 N2 。 根据渐开线的性质可知: K1 K1 v ⊥ r , 1 1 b1 N K ⊥ N r ,所以 N2KvK1 = N1O1K = K1 同理, N2KvK2 = N2O2K = K2。 因为两齿轮在 K 点的公法线 n-n 方向上的速度是相同的,所以 K1 K1 K2 K2 v cos = v cos 又因为 K1 1 K1 v = r , K2 2 K2 v = r ,所以 K1 1 K1 K2 2 K2 r cos = r cos 将 K1 K1 b1 r cos = r , K2 K2 b2 r cos = r 代入上式可得 b11 b22 r = r 再将这一结果代入式(6-1)得 b1 b2 2 1 12 r r i = = (6-14) 综合上述分析过程,可见渐开线齿轮具有如下传动特性: 1)传动比恒定 由式(6-14)可知,渐开线齿廓的齿轮在任意点 K 处啮合时,其传动比 i 都等于两齿轮基圆 半径的反比,是个常量,所以在传动过程中,传动比是个恒定值。 2)中心距具有可分性 由于渐开线齿轮的传动比只与两齿轮的基圆半径相关,而一对齿轮加工完成后,两齿轮的基 圆半径就确定了,所以其传动比也就确定了。如果由于制造、安装或磨损等原因造成中心距发生 了变动,传动比也不会随之变化。这一特性称为渐开线齿轮的中心距可分性,它为齿廓的加工和 齿轮的安装等带来很大的方便,是渐开线齿轮得到广泛应用的原因之一。 3)传力方向不变 两齿廓的接触点 K 的公法线始终与两个齿轮的基圆相切(为两基圆的公切线),而当两个齿 轮安装好之后,基圆的公切线 n-n 的位置也随之确定。也就是说两齿廓啮合时的正压力方向(沿 n-n)始终不变,这个特点对于齿轮传动过程中的平稳性是非常有利的。 6.5.2 渐开线齿轮的正确啮合条件 如图 6-20 所示为一对渐开线齿轮的啮合情况。如前所述,一对渐开线齿廓在任意位置啮合 时,其接触点都应在啮合线 N1N2 上。因此当上一对轮齿在啮合线上 B1 点接触时,下一对轮齿的 啮合点 B2 也应该在 N1N2 上。由此可以看出,两齿轮能够正确啮合的条件应该是:两齿轮的法 向间距相等,即
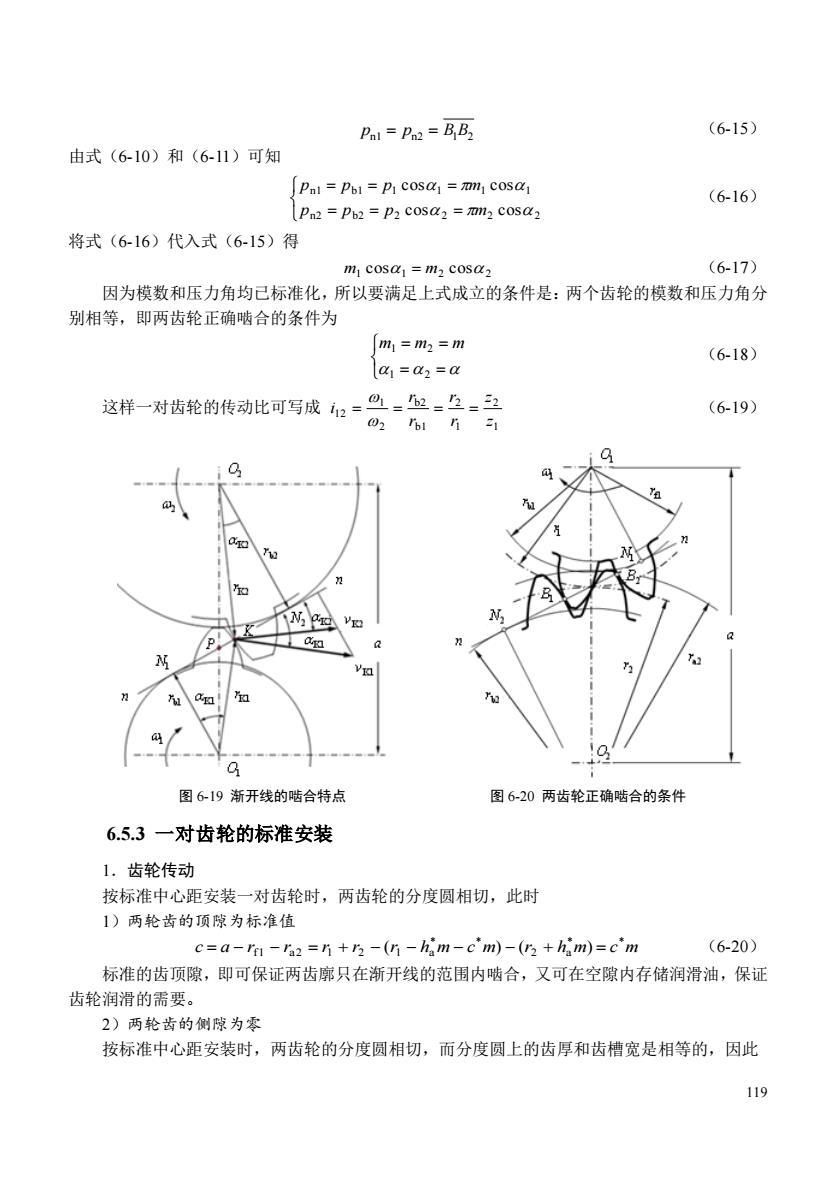
Pal Pn2 =BB (615) 由式(6-10)和(6-11)可知 Pal =Pol =P cosa =mm cosa (6-16) Pn2 =Pb2 P2 cosa2 =2 cosa2 将式(6-16)代入式(6-15)得 m cosa=m,cosa (6-17) 因为模数和压力角均己标准化,所以要满足上式成立的条件是:两个齿轮的模数和压力角分 别相等,即两齿轮正确啮合的条件为 m =m2 =m (6-18) la=a2=a 这样一对齿轮的传动比可写成2==位=2=三 (6-19) 02n1h51 图619渐开线的啮合特点 图620两齿轮正确啮合的条件 6.5.3一对齿轮的标准安装 1.齿轮传动 按标准中心距安装一对齿轮时,两齿轮的分度圆相切,此时 1)两轮齿的顶隙为标准值 c=a-ra-n2=n+r-(n-him-c'm)-(r2 +him)=c'm (6-20) 标准的齿顶隙,即可保证两齿廓只在渐开线的范围内啮合,又可在空隙内存储润滑油,保证 齿轮润滑的需要, 2)两轮齿的侧隙为零 按标准中心距安装时,两齿轮的分度圆相切,而分度圆上的齿厚和齿槽宽是相等的,因此 119
119 pn1 = pn2 = B1B2 (6-15) 由式(6-10)和(6-11)可知 = = = = = = n2 b2 2 2 2 2 n1 b1 1 1 1 1 cos cos cos cos p p p m p p p m (6-16) 将式(6-16)代入式(6-15)得 1 1 2 2 m cos = m cos (6-17) 因为模数和压力角均已标准化,所以要满足上式成立的条件是:两个齿轮的模数和压力角分 别相等,即两齿轮正确啮合的条件为 = = = = 1 2 m1 m2 m (6-18) 这样一对齿轮的传动比可写成 1 2 1 2 b1 b2 2 1 12 z z r r r r i = = = = (6-19) 图 6-19 渐开线的啮合特点 图 6-20 两齿轮正确啮合的条件 6.5.3 一对齿轮的标准安装 1.齿轮传动 按标准中心距安装一对齿轮时,两齿轮的分度圆相切,此时 1)两轮齿的顶隙为标准值 c a r r r r r h m c m r h m c m * * 2 a * * f1 a2 1 2 1 a = − − = + − ( − − ) − ( + ) = (6-20) 标准的齿顶隙,即可保证两齿廓只在渐开线的范围内啮合,又可在空隙内存储润滑油,保证 齿轮润滑的需要。 2)两轮齿的侧隙为零 按标准中心距安装时,两齿轮的分度圆相切,而分度圆上的齿厚和齿槽宽是相等的,因此

=6-2m: 因两齿轮模数相等,所以 S1=e1=5:=e2 (6-21) 也就是说,一个齿轮的齿厚等于另一个齿轮的齿槽宽度,所以可以实现无侧隙啮合。 在实际使用时,两齿轮的非受力齿侧间是需要有一些间隙的。但这个间隙量很小,是通过制 造公差来实现的。 按标准中心距安装后,齿侧间隙为零,所以实际安装的中心距a不可能小于标准中心距。 当实际中心距a大于标准中心距α时,两个齿轮的分度圆将不再相切,齿顶隙大于标准值,齿 侧存在间隙,过节点的节圆的半径r大于分度圆的半径,如图6-21所示。 因n=rcosa=rcosa',所以i+n2=(G+2)cosa=('+n2')cosd,即 a'coso'=acoso (6-22) 上式表明了节圆上的压力角(也称啮合角)随中心距变化的关系 需要注意的是:节圆是两齿轮啮合传动时才有的,其大小与中心距的变化有关,单个齿轮没 有节圆:但是不论齿轮是否参与呐合传动,分度圆是单个齿轮所固有的、大小确定的圆,与传动 中心距的变化无关。当标准齿轮按照标准中心距安装时,节圆与分度圆重合:而当两齿轮实际中 心距大于标准中心距a时,两齿轮的节圆虽相切,但分度圆却相互分离 2.齿轮与齿条传动 齿轮齿条的标准安装与齿轮传动标准中心距安装类似,即安装后齿条的分度线与齿轮的分度 圆相切。 如图622所示,当齿轮与齿条的距离加大时,因为齿条的压力角处处相等,所以啮合点的 公法线-的方向仍然保持不变,即O,P的距离不变,所以齿轮的节点位置仍然与在分度圆上, 但齿条的分度线位置已经改变,齿条节圆上的齿槽宽大于其分度圆上的齿槽宽。 由此得到齿轮齿条传动的特点: (1)无论是否按标准中心距安装,齿轮的节圆恒与分度圆重合。 (2)啮合角恒等于分度圆压力角a (3)当实际安装距离大于标准安装距离时,齿顶隙大于标准值,齿侧存在间隙。 120
120 2 1 2 1 2 2 2 1 1 1 s e m s e m = = = = 因两齿轮模数相等,所以 1 1 2 2 s = e = s = e (6-21) 也就是说,一个齿轮的齿厚等于另一个齿轮的齿槽宽度,所以可以实现无侧隙啮合。 在实际使用时,两齿轮的非受力齿侧间是需要有一些间隙的。但这个间隙量很小,是通过制 造公差来实现的。 按标准中心距安装后,齿侧间隙为零,所以实际安装的中心距 a' 不可能小于标准中心距 a。 当实际中心距 a' 大于标准中心距 a 时,两个齿轮的分度圆将不再相切,齿顶隙大于标准值,齿 侧存在间隙,过节点的节圆的半径 r' 大于分度圆的半径 r,如图 6-21 所示。 因 cos 'cos ' rb = r = r ,所以 ( ) cos ( ' ') cos ' rb1 + rb2 = r1 + r2 = r1 +r2 ,即 a'cos' = a cos (6-22) 上式表明了节圆上的压力角 ' (也称啮合角)随中心距变化的关系。 需要注意的是:节圆是两齿轮啮合传动时才有的,其大小与中心距的变化有关,单个齿轮没 有节圆;但是不论齿轮是否参与啮合传动,分度圆是单个齿轮所固有的、大小确定的圆,与传动 中心距的变化无关。当标准齿轮按照标准中心距安装时,节圆与分度圆重合;而当两齿轮实际中 心距 a' 大于标准中心距 a 时,两齿轮的节圆虽相切,但分度圆却相互分离。 2.齿轮与齿条传动 齿轮齿条的标准安装与齿轮传动标准中心距安装类似,即安装后齿条的分度线与齿轮的分度 圆相切。 如图 6-22 所示,当齿轮与齿条的距离加大时,因为齿条的压力角处处相等,所以啮合点的 公法线 n-n 的方向仍然保持不变,即 O1P 的距离不变,所以齿轮的节点位置仍然与在分度圆上, 但齿条的分度线位置已经改变,齿条节圆上的齿槽宽大于其分度圆上的齿槽宽。 由此得到齿轮齿条传动的特点: (1)无论是否按标准中心距安装,齿轮的节圆恒与分度圆重合。 (2)啮合角 ' 恒等于分度圆压力角 。 (3)当实际安装距离大于标准安装距离时,齿顶隙大于标准值,齿侧存在间隙