《自动控制原理》课程教学资源（电子教案）第三章 线性系统的时域分析法

二阶系统的动态特性，可以用=和の这两个参量的形式加以描述二阶系统的特征方程：$? +250,S+0,=0(3-19)St2 =-50, ±0,V5?-1(3-20)3.3.2二阶系统的单位阶跃响应阻尼比是实际阻尼系数F与临界阻尼系数F的比值111FF=2/TK-2JJK/F2JJK-F2/JK/F2Fc一临界阻尼系数，=1时，阻尼系数发散<0两个正实部的特征根0<<1，闭环极点为共扼复根，位于右半S平面，这时的系统叫做欠阻尼系统5=1，为两个相等的根>1，两个不相等的根=0，虚轴上，瞬态响应变为等幅振荡S=0右半平面<0jo左半平面>0Ajon0<<1不ε=1两个相等根Od=Ony1-E￥*va=0E>1jon两个不等根图3-9二阶系统极点分布(1)欠阻尼（0<<1)二阶系统的单位阶跃响应Si,2 =-5o, ±jo, V1-5?令=,—衰减系数0=の,/1-≤2-阻尼振荡频率=-α±jod59

59 二阶系统的动态特性，可以用  和 n 这两个参量的形式加以描述 二阶系统的特征方程： 2 0 2 2 S + n S +n = （3-19） 1 2 S1,2 = −n n  − （3-20） 3.3.2 二阶系统的单位阶跃响应 阻尼比  是实际阻尼系数 F 与临界阻尼系数 FC 的比值 m FC F JK F J K F T K J K F = = = = = 1 2 1 2 2 1 2 1 2 1  FC －临界阻尼系数，  = 1 时，阻尼系数   0 两个正实部的特征根 发散 0    1 ，闭环极点为共扼复根，位于右半 S 平面，这时的系统叫做欠阻尼系统  = 1 ，为两个相等的根   1 ，两个不相等的根  = 0 ，虚轴上，瞬态响应变为等幅振荡 图 3-9二 阶 系 统 极 点 分 布 左 半 平 面 ξ>0 0<ξ<1 ξ=1 两 个 相 等 根 jωn ξ=0 ωd=ωn σ jωn β ξ=0 jω 右 半 平 面 ξ<0 ξ>1 两 个 不 等 根 0 (1)欠阻尼( 0    1 )二阶系统的单位阶跃响应 2 S1,2 = −n  jn 1− 令  = n －衰减系数 d = −  j 2  d =  n 1− －阻尼振荡频率

1由式（3-18）得R(s)=S0,?1C(s)=Φ(s)R(s) :$?+250,S+0S1S+50.Eon5SonSon=Odd0$ ($+50,)?+0d?odOnVi-g?(S+E0,)? +0dV1-22V1-2β5对上式取拉氏反变换，得单位阶跃响应为Eh(t)=1-e-5or[cosoat+sinoat]1-521e" sin(Oat + β)(3-21)1≥0=/i-稳态分量瞬态分量Vi-g2β=arctg=arccos5稳态分量为1，表明图3-8系统在单位阶跃函数作用下，不存在稳态位置误差，瞬态分量为阻尼正弦振荡项，其振荡频率为の，一阻尼振荡频率包络线1±e-0//1-≤?决定收敛速度(3-23)=0时,h(t)=1-sinのntt≥0这是一条平均值为1的正、余弦形式等幅振荡，其振荡频率为の，一故称为无阻尼振荡频率。の,由系统本身的结构参数K和T，，或K和J确定，の，常称自然频率。·实际控制系统通常有一定的阻尼比，因此不可能通过实验方法测得の。，而只能测得のa，且a<の，≥1,のa不复存在，系统的响应不再出现振荡。(2)临界阻尼(=1)1r(0)= u(t) ， R(s)=S60

60 S R s 1 ( ) = ，由式（3-18）得 S S S C s s R s n n n 1 2 ( ) ( ) ( ) 2 2 2  + + = =      2 2 2 2 ( ) ( ) 1 n d n n d n S S S S           + + − + + + = − 2 2 1 1             − = − = d n n d d n d 对上式取拉氏反变换，得单位阶跃响应为 1  2 1−  sin ] 1 ( ) 1 [cos 2 h t e t t d d t n      − = − + − sin( ) 0 1 1 1 2 +  − = − − e t t d t n     （3-21） 稳态分量 瞬态分量     arccos 1 2 = − = arctg 稳态分量为 1，表明图 3-8 系统在单位阶跃函数作用下，不存在稳态位置误差，瞬 态分量为阻尼正弦振荡项，其振荡频率为  d －阻尼振荡频率 包络线 2 1 1    − − t n e 决定收敛速度  = 0 时， h(t) =1− sin n t t  0 （3-23） 这是一条平均值为 1 的正、余弦形式等幅振荡，其振荡频率为 n －故称为无阻尼 振荡频率。 n 由系统本身的结构参数 K 和 Tm ，或 K1 和 J 确定， n 常称自然频率。 ·实际控制系统通常有一定的阻尼比，因此不可能通过实验方法测得 n ，而只能 测得  d ，且 d n ，  d  1, 不复存在，系统的响应不再出现振荡。 (2)临界阻尼(  = 1 ) S r t u t R s 1 ( ) = ( ) , ( ) =

0?111O,C(s)=(S+o,)ss(S+o,)?S+0临界阻尼情况下的二阶系统的单位阶跃响应称为临界阻尼响应h(t)=1-e-"o,t-e-=1-e-(1+,t)1≥0(3-24)当=1时，二阶系统的单位阶跃响应是稳态值为1的无超调单调上升过程，dh(t)?+e-r0.dt(3)过阻尼(5>1)Si2=-50,±0,VE?-1o.?QC(s) =(S-S,)(S-S,) S"[S+0,(5- /52-1)[S+0,(5+52-1)]SA2MAsS+0,(5-V52-1) 5+0,(5+V52-1)A, =1-1AS+0,(5-VE?-1)1A, =2152 -1(5 + 52 -1)1e-(5+/F-1)e 1≥0(5-/52-1)0h(t)=1-2/52-1(5- 52-1)2/52-1(5 +V52-1)(3-25)jo慢衰减快A1/7??0S2Si v4基本上由S1决定$图3-10二阶系统的实极点61

61 n n n n n S S S S S C s      + − +  = − + = 1 ( ) 1 1 ( ) ( ) 2 2 2 临界阻尼情况下的二阶系统的单位阶跃响应称为临界阻尼响应 ( ) = 1− − = 1− (1+ )  0 − − − h t e t e e t t n t t n t n  n n     （3-24） 当  = 1 时，二阶系统的 单位阶跃响 应是稳态值 为 1 的无超调 单调上升过 程， t n n e dt dh t   − = + ( ) 2 (3)过阻尼(   1 ) 1 2 S1,2 = −n n  − S S S S S S S S C s n n n n [ ( 1)][ ( 1)] 1 ( )( ) ( ) 2 2 2 1 2 2 + − − + + −  = − − =         ( 1) ( 1) 2 3 2 1 2 + + − + + − − = + n    n   A S A S A A1 =1 ( 1) 1 2 2 + − − − = S  n   A 2 1( 1) 1 2 2 3 − + − =    A 0 2 1( 1) 1 2 1( 1) 1 ( ) 1 ( 1) 2 2 ( 1) 2 2 2 2  − + − + − − − = − − − − − + − h t e e t t t   n   n       （3-25） jω S2 S1 衰减快 慢 ξ 基 本 上 由 S1决 定 图 3-10二 阶 系 统 的 实 极 点 σ 0

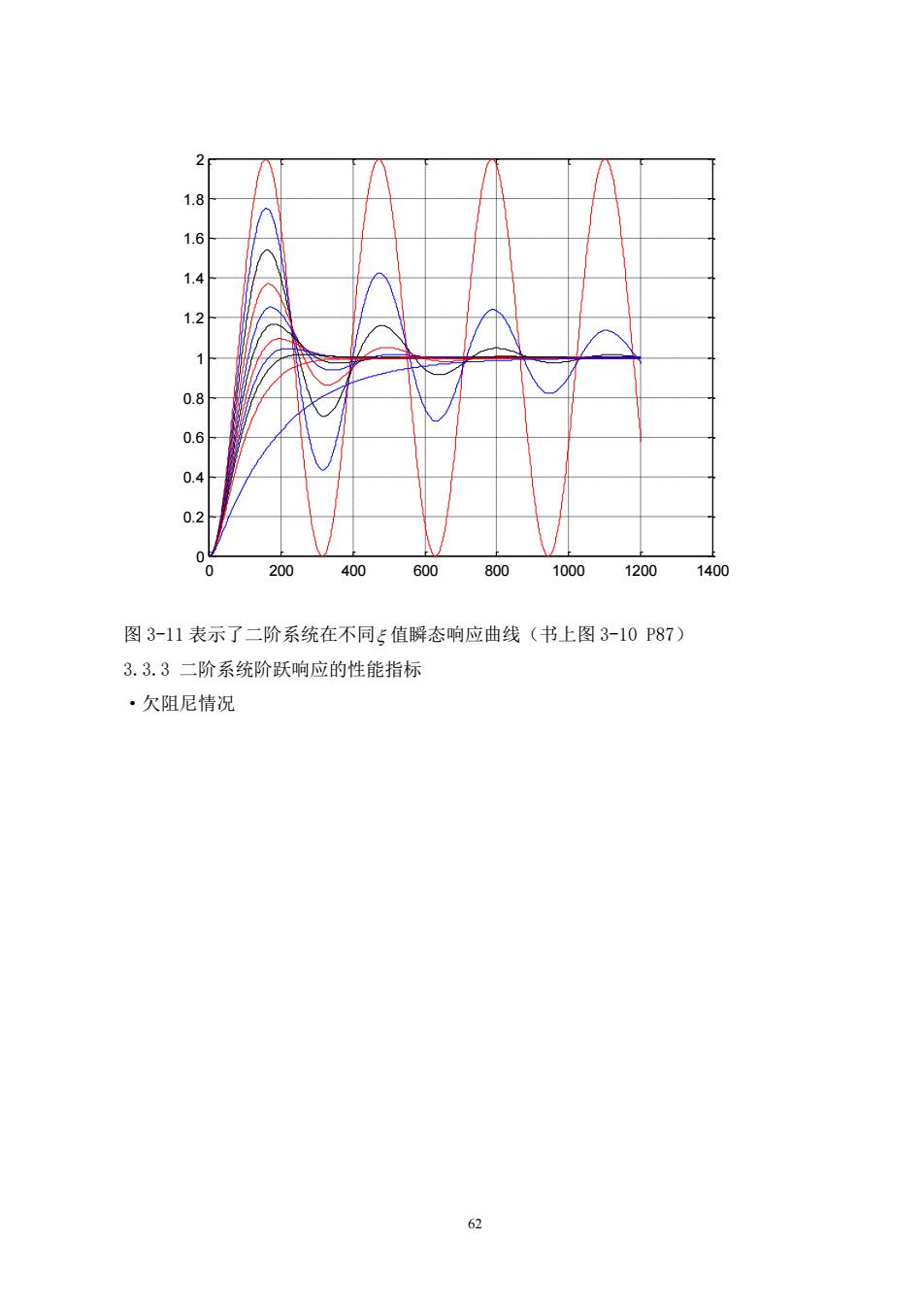
11.81.61.41.20.80.60.40.220200400600800100012001400图3-11表示了二阶系统在不同=值瞬态响应曲线（书上图3-10P87）3.3.3二阶系统阶跃响应的性能指标·欠阻尼情况62

62 0 200 400 600 800 1000 1200 1400 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 图 3-11 表示了二阶系统在不同  值瞬态响应曲线（书上图 3-10 P87） 3.3.3 二阶系统阶跃响应的性能指标 ·欠阻尼情况

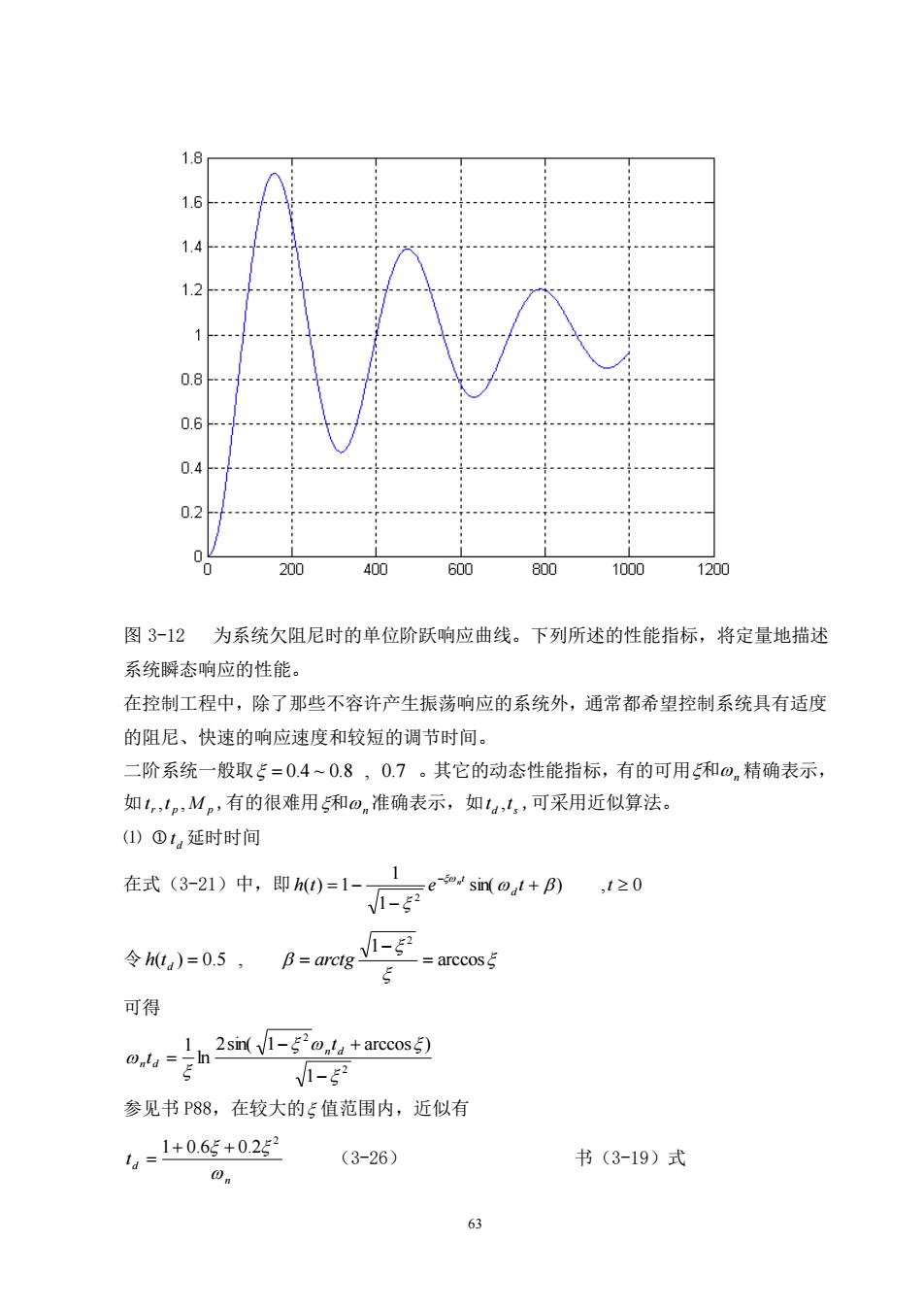
1.81.61.41.20.80.60.4 0.2 .--.0020040060080010001200图3-12为系统欠阻尼时的单位阶跃响应曲线。下列所述的性能指标，将定量地描述系统瞬态响应的性能。在控制工程中，除了那些不容许产生振荡响应的系统外，通常都希望控制系统具有适度的阻尼、快速的响应速度和较短的调节时间。二阶系统一般取=0.4～0.8，0.7。其它的动态性能指标，有的可用和の,精确表示，如tr，t,M，，有的很难用和の，准确表示，如ta，t，可采用近似算法。(1)①t延时时间1在式（3-21）中，即h(t)=1-So sin(Oat + β),t≥0/1-52V-2令h(ta)=0.5,β=arctg=arccos5可得1, 2sin(/1-$o,ta +arccos)Wnta=-ln5Vi-5?参见书P88，在较大的值范围内，近似有I = 1+0.6§ + 0.252(3-26)书（3-19）式On63

63 图 3-12 为系统欠阻尼时的单位阶跃响应曲线。下列所述的性能指标，将定量地描述 系统瞬态响应的性能。 在控制工程中，除了那些不容许产生振荡响应的系统外，通常都希望控制系统具有适度 的阻尼、快速的响应速度和较短的调节时间。 二阶系统一般取  = 0.4 ~ 0.8 , 0.7 。其它的动态性能指标，有的可用 和n 精确表示， 如 r p M p t ,t , ,有的很难用 和n 准确表示，如 d s t ,t ,可采用近似算法。 ⑴  d t 延时时间 在式（3-21）中，即 sin( ) , 0 1 1 ( ) 1 2 +  − = − − h t e t t d t n     令     arccos 1 ( ) 0.5 , 2 = − h t d = = arctg 可得 2 2 1 2sin( 1 arccos ) ln 1       − − + = n d n d t t 参见书 P88，在较大的  值范围内，近似有 n d t    2 1+ 0.6 + 0.2 = （3-26） 书（3-19）式